近年，随着有监督学习的低枝果实被采摘的所剩无几，无监督学习成为了研究热点。VAE（Variational Auto-Encoder，变分自编码器）[1,2] 和 GAN（Generative Adversarial Networks） 等模型，受到越来越多的关注。

笔者最近也在学习 VAE 的知识（从深度学习角度）。首先，作为工程师，我想要正确的实现 VAE 算法，以及了解 VAE 能够帮助我们解决什么实际问题；作为人工智能从业者，我同时希望在一定程度上了解背后的原理。

作为学习笔记，本文按照由简到繁的顺序，首先介绍 VAE 的具体算法实现；然后，再从直观上解释 VAE 的原理；最后，对 VAE 的数学原理进行回顾。我们会在适当的地方，对变分、自编码、无监督、生成模型等概念进行介绍。

我们会看到，同许多机器算法一样，VAE 背后的数学比较复杂，然而，工程实现上却非常简单。

1. 算法实现

这里介绍 VAE 的一个比较简单的实现，尽量与文章[1] Section 3 的实验设置保持一致。完整代码可以参见 repo。

1.1 输入：

数据集 $X \subset R^n$。

做为例子，可以设想 $X$ 为 MNIST 数据集。因此，我们有六万张 0~9 的手写体 的灰度图（训练集）， 大小为 $28 \times 28$。进一步，将每个像素归一化到$[0, 1]$，则 $X \subset [0, 1]^{784}$ 。

图1. MNIST demo （图片来源）

1.2 输出：

一个输入为 $m$ 维，输出为 $n$ 维的神经网络，不妨称之为 decoder [1]（或称 generative model [2]）（图1）。

图 2. decoder

• 在输入输出维度满足要求的前提下，decoder 以为任何结构——MLP、CNN，RNN 或其他。
• 由于我们已经将输入数据规一化到 [0, 1] 区间，因此，我们令 decoder 的输出也在这个范围内。这可以通过在 decoder 的最后一层加上 sigmoid 激活实现 :
  $$f(x)=\frac{1}{1+e^{-x}}$$
• 作为例子，我们取 m = 100，decoder 的为最普遍的全连接网络（MLP）。基于 Keras Functional API 的定义如下：

n, m = 784, 2
hidden_dim = 256
batch_size = 100

## Encoder
z = Input(batch_shape=(batch_size, m))
h_decoded = Dense(hidden_dim, activation=‘tanh‘)(z)
x_hat = Dense(n, activation=‘sigmoid‘)(h_decoded)

1.3 训练

图 3. VAE 结构框架

1.3.1 encoder

为了训练 decoder，我们需要一个辅助的 encoder 网络（又称 recognition model）（如图3）。encoder 的输入为 $n$ 维，输出为 $2\times m$ 维。同 decoder 一样，encoder 可以为任意结构。

图 4. encoder

1.3.2 采样（sampling）

我们将 encoder 的输出（$2\times m$ 个数）视作分别为 $m$ 个高斯分布的均值（z_mean）和方差的对数（z_log_var）。

接着上面的例子，encoder 的定义如下：

## Encoder
x = Input(batch_shape=(batch_size, n))
h_encoded = Dense(hidden_dim, activation=‘tanh‘)(x)
z_mean = Dense(m)(h_encoded)    # 均值
z_log_var = Dense(m)(h_encoded) # 方差对数

然后，根据 encoder 输出的均值与方差，生成服从相应高斯分布的随机数：

epsilon = K.random_normal(shape=(batch_size, m), 
                          mean=0.,std=epsilon_std) # 标准高斯分布
z = z_mean + exp(z_log_var / 2) * epsilon

$z$ 就可以作为上面定义的 decoder 的输入，进而产生 $n$ 维的输出 $\hat{x}$。

图5. 采样

这里运用了 reparemerization 的技巧。由于 $z \sim N(\mu, \sigma)$，我们应该从 $N(\mu, \sigma)$ 采样，但这个采样操作对 $\mu$ 和 $\sigma$ 是不可导的，导致常规的通过误差反传的梯度下降法（GD）不能使用。通过 reparemerization，我们首先从 $N(0, 1)$ 上采样 $\epsilon$，然后，$z = \sigma\cdot\epsilon + \mu$。这样，$z \sim N(\mu, \sigma)$，而且，从 encoder 输出到 $z$，只涉及线性操作，（$\epsilon$ 对神经网络而言只是常数），因此，可以正常使用 GD 进行优化。方法正确性证明见[1] 2.3小节和[2] 第3节 （stochastic backpropagation）。

图6. Reparameterization （图片来源）

preparameterization 的代价是隐变量必须连续变量[7]。

1.3.3 优化目标

encoder 和 decoder 组合在一起，我们能够对每个 $x \in X$，输出一个相同维度的 $\hat{x}$。我们目标是，令 $\hat{x}$ 与 $x$ 自身尽量的接近。即 $x$ 经过编码（encode）后，能够通过解码（decode）尽可能多的恢复出原来的信息。

注：严格而言，按照模型的假设，我们要优化的并不是 $x$ 与 $\hat{x}$ 之间的距离，而是要最大化 $x$ 的似然。不同的损失函数，对应着不是 $p(x|z)$ 的不同概率分布假设。此处为了直观，姑且这么解释，详细讨论见下文（[1] 附录C）。

由于 $x \in [0, 1]$，因此，我们用交叉熵（cross entropy）度量 $x$ 与 $\hat{x}$ 差异：

$$xent = \sum_{i=1}^n-[x_i\cdot\log(\hat{x}_i)+(1-x_i)\cdot\log(1-\hat{x}_i)]$$

xent 越小，$x$ 与 $\hat{x}$ 越接近。

我们也可以用均方误差来度量：

$$mse=\sum_{i=1}^n(x_i - \hat{x}_i)^2$$
mse 越小，两者越接近。

训练过程中，输出即是输入，这便是 VAE 中 AE（autoencoder，自编码）的含义。

另外，我们需要对 encoder 的输出 z_mean（$\mu$）及 z_log_var（$\log\sigma^2$）加以约束。这里使用的是 KL 散度（具体公式推导见下文）：

$$KL = -0.5 * (1+\log\sigma^2-\mu^2-\sigma^2)=-0.5(1+\log\sigma^2-\mu^2-exp(\log\sigma^2))$$

这里的KL， 其实是 KL 散度的负值，见下文。

总的优化目标（最小化）为：

$$loss = xent + KL$$

或

$$loss = mse + KL$$

综上所述，有了目标函数，并且从输入到输出的所有运算都可导，我们就可以通过 SGD 或其改进方法来训练这个网络了。

由于训练过程只用到 $x$（同时作为输入和目标输出），而与 $x$ 的标签无关，因此，这是无监督学习。

1.4 小结

总结一下，如图2，VAE 包括 encoder （模块 1）和 decoder（模块 4） 两个神经网络。两者通过模块 2、3 连接成一个大网络。利益于 reparemeterization 技巧，我们可以使用常规的 SGD 来训练网络。

学习算法的最好方式还是读代码，网上有许多基于不同框架的 VAE 参考实现，如 tensorflow、theano、keras、torch。

2. 直观解释

2.1 VAE 有什么用？

2.1.1 数据生成

由于我们指定 $p(z)$ 标准正态分布，再接合已经训练和的 decoder （$p(x|z)$），就可以进行采样，生成类似但不同于训练集数据的新样本。

图7. 生成新的样本

图8（交叉熵）和图9（均方误差）是基于训练出来的 decoder，采样生成的图像（$\hat{x}$）

图8. 交叉熵损失

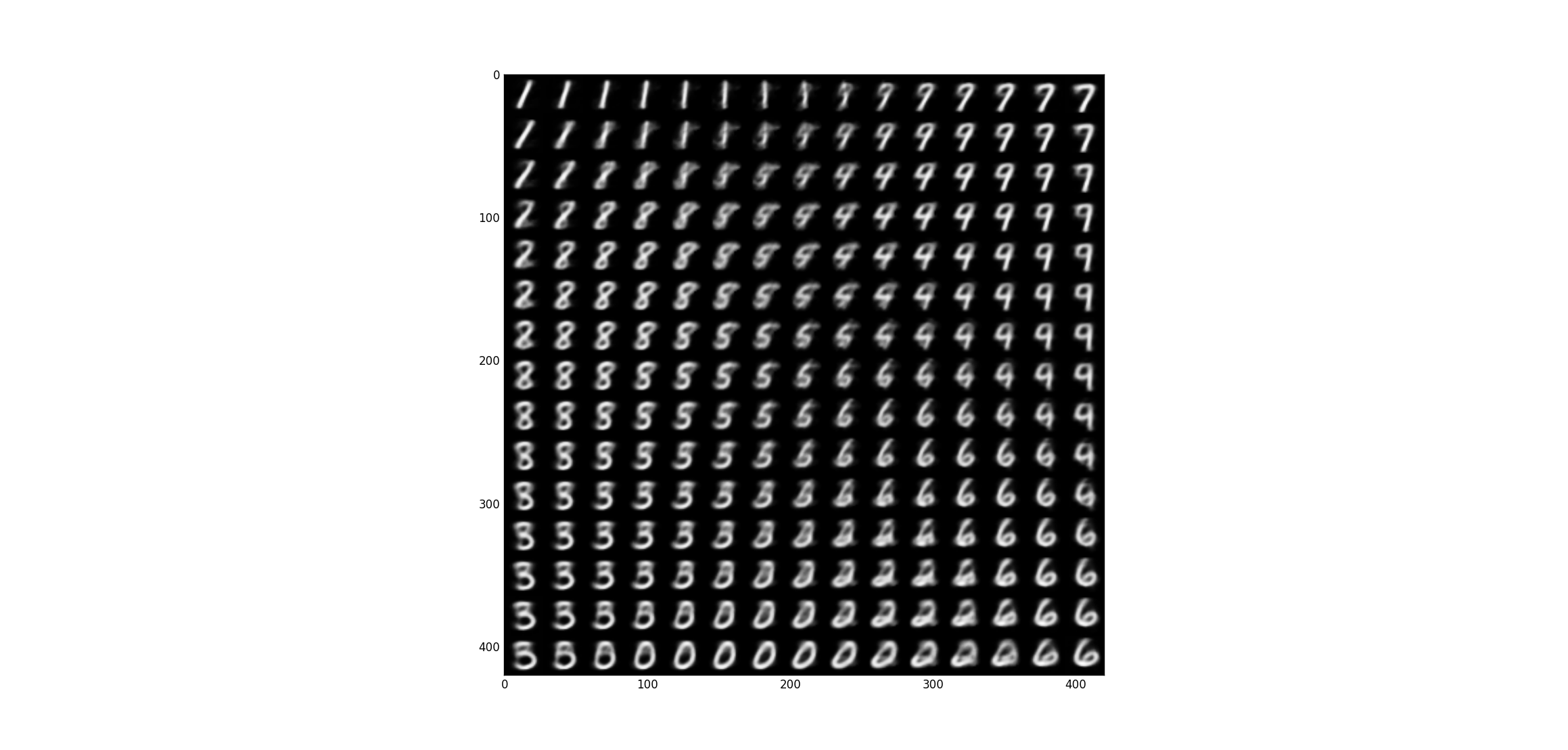
图9. 均方误差损失

严格来说，生成上图两幅图的代码并不是采样，而是 $E[x|z]$ 。伯努力分布和高斯分布的期望，正好是 decocder 的输出 $\hat{x}$。见下面的讨论。

2.1.2 高维数据可视化

encoder 可以将数据 $x$，映射到更低维的 $z$ 空间，如果是2维或3维，就可以直观的展示出来（图10、11）。

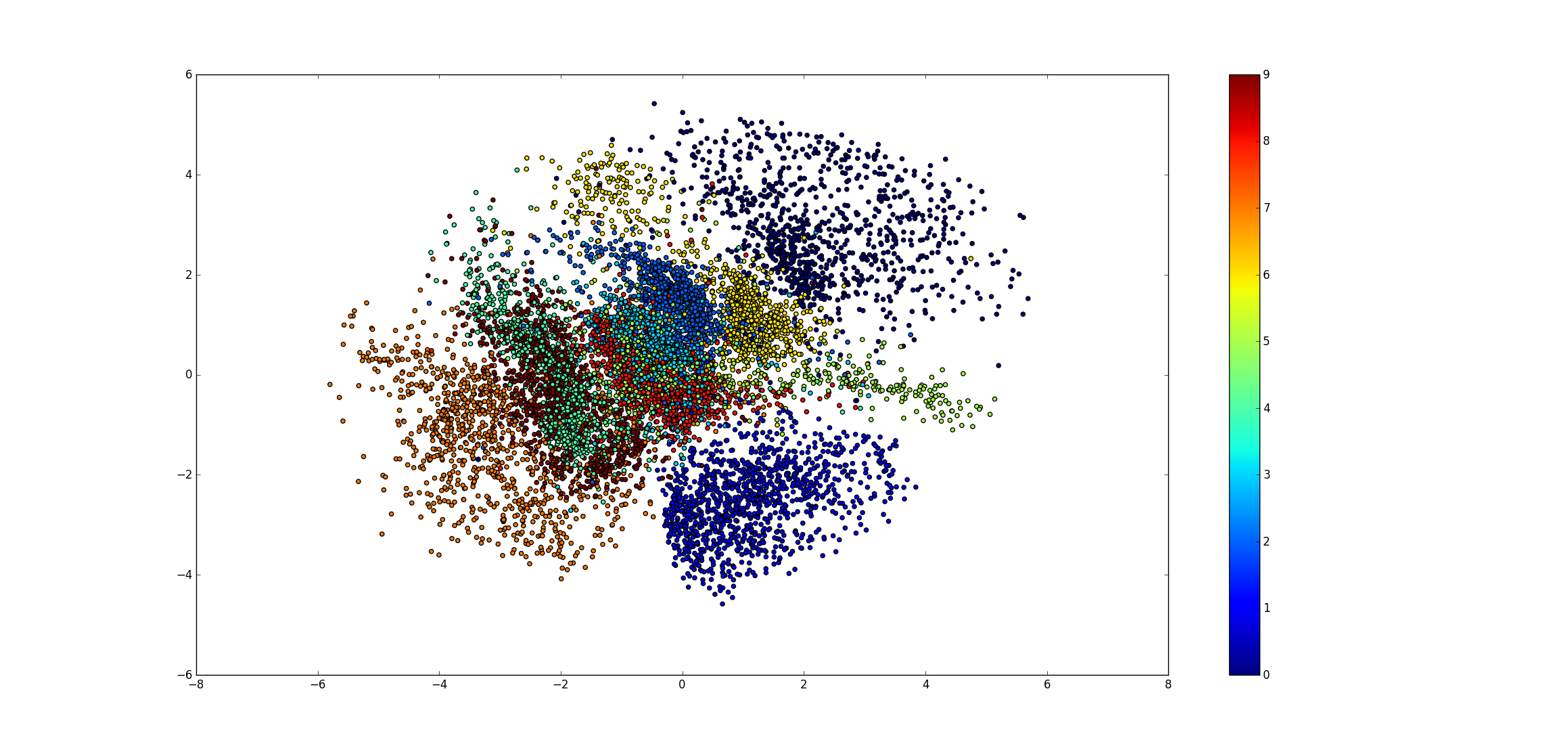
图10. 交叉熵损失

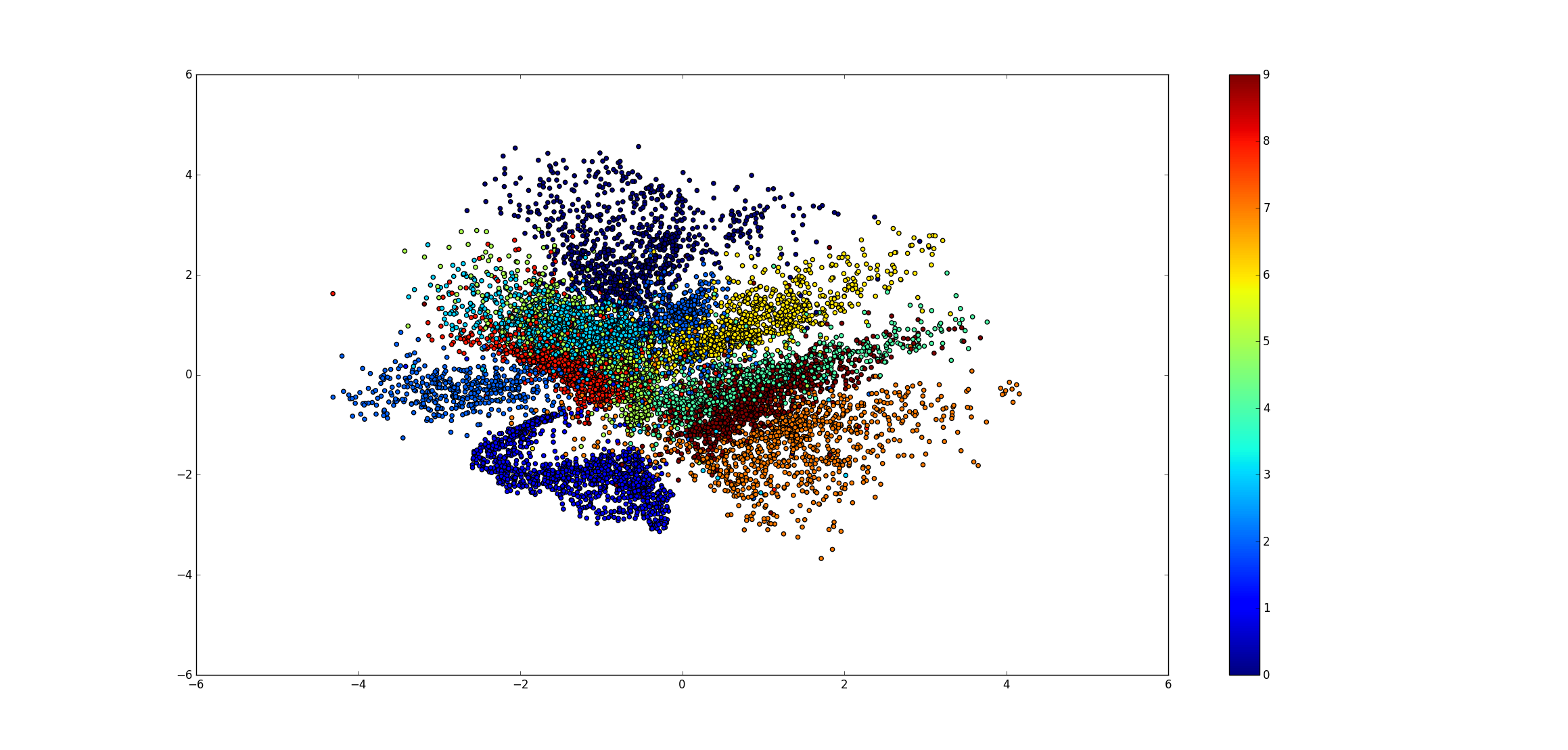
图11. 均方误差损失

2.1.3 缺失数据填补（imputation）

对许多现实问题，样本点的各维数据存在相关性。因此，在部分维度缺失或不准确的情况，有可能通过相关信息得到填补。图12、13展示一个简单的数据填补的实例。其中，第一行为原图，第二行为人行中间某些像素的缺失图，第三行为利用 VAE 模型恢复的图。

图12. 交叉熵损失

图13. 均方误差损失

2.1.4 半监督学习

相比于高成本的有标注的数据，无标注数据更容易获取。半监督学习试图只用一小部分有标注的数据加上大量无标注数据，来学习到一个较好预测模型（分类或回归）。
VAE 是无监督的，而且也可以学习到较好的特征表征，因此，可以被用来作无监督学习[3, 12]。

2.2 VAE 原理

由于对概率图模型和统计学等背景知识不甚了了，初读[1, 2]，对问题陈述、相关工作和动机完全无感。因此，先放下公式，回到 comfort zone，类比熟悉的模型，在直觉上理解 VAE 的工作原理。

2.2.1 模型结构

从模型结构（以及名字）上看，VAE 和 自编码器（audoencoder）非常的像。特别的，VAE 和 CAE（constractive AE）非常相似，两者都对隐层输出增加长约束。而 VAE 在隐层的采样过程，起到和 dropout 类似的正则化偷用。因此，VAE 应该和 CAE 有类似的训练和工作方式，并且不太易容过拟合。

2.2.2 流形学习

数据虽然高维，但相似数据可能分布在高维空间的某个流形上（例如图14）。而特征学习就要显式或隐式地学习到这种流形。

图14. 流形学习 （图片来源）

正是这种流形分布，我们才能从低的隐变量恢复出高维的观测变量。如图8、图9，相似的隐变量对应的观测变量确实比较像，并且这样相似性是平滑的变化。

3. 推导

VAE 提出背景涉及概率领域的最大似然估计（最大后验概率估计）、期望最大化（EM）算法、变分推理（variational inference，VI）、KL 散度，MCMC 等知识。但 VAE 算法本身的数学推导不复杂，如果熟悉各个内容的话，可以直接跳到 3.6。

3.1 问题陈述

已知变量 $x$ 服从某固定但未知的分布。$x$ 与隐变量（latent variables）的关系可以用图15 描述。这是一个简单的概率图。（注意，$x$ 和 $z$ 都是向量）

图15 两层的有向概率图，x为观测变量，z为隐变量

对于这个概率图，$p(z)$ （隐变量 $z$ 的先验）、$p(x|z)$（$x$ 相对 $z$ 的条件概率）,及 $p(z|x)$（隐变量后验）三者就可行完全描述 $x$ 和 $z$ 之间的关系。因为两者的联合分布可以表示为：

$$p(z,x) = p(x|z)p(z)$$

$x$ 的边缘分布可以计算如下：

$$p(x) = \int_z p(x, z)dz = \int_z p(x|z) \cdot p(z)dz = E_z[p(x|z)]$$

我们只能观测到 $x$，而 $z$ 是隐变量，不能被观测。我们任务便是通过一个观察集 $X$，估计概率图的相关参数。

对于一个机器学习模型，如果它能够（显式或隐式的）建模 $p(z)$ 和 $p(x|z)$，我们就称之为生成模型。这有如下两层含义：
1. 两者决定了联合分布 $p(x, z)$；
2. 利用两者可以对 x 进行采样（ancestral sampling）。具体方法是，先依概率生成样本点 $z_i\sim p(z)$，再依概率采样 $x_i \sim p(x|z_i)$。

最简单的生成模型可能是朴素贝叶斯模型。

3.2 最大似然估计（Maximum Likelihood Estimation，MLE）

概率分布的参数最经典的方法是最大似然估计。

给定一组观测值

$$X = (x_i),\ i = 1,..,n$$ 。观测数据的似然为：
$$L(p_\theta(X)) = \prod_i^np_\theta(x_i)$$

一般取似然的对数：

$$\log L(p_\theta(X)) = \sum_i^n\log p_\theta(x_i)$$

MLE 假设最大化似然的参数 $\theta^*$ 为最优的参数估计。因此，概率的参数估计问题转化为了最大化 $\log L(p_\theta(X))$ 的最化问题。

从贝叶斯推理的观点，$\theta$ 本身也是随机变量，服从某分布 $p(\theta)$。

$$p(\theta|X) = \frac{p(\theta)\cdotp(X|\theta)}{p(X)}=\frac{p(\theta)\cdotp(X|\theta)}{\int_\theta p(X, \theta)d\theta} \propto p(\theta)\cdotp(X|\theta)$$

$$\log p(\theta|X) = \log p(\theta) + \log L(p(X|\theta))$$

这是最大后验概率估计（MAP）。

3.3 期望最大化算法（Expectation-Maximum，EM）

对于我们问题，利用 MLE 准则，优化目标为：

$$\log p(X, Z)$$

由于$z$ 不可观测， 我们只能设法优化：

$$\log p(X) = \log \int_z p(X, z) dz$$

通过 MLE 或 MAP 现在我们已经有了要目标（对数似然），但在我们问题下，似然中存在对隐变量 $\mathbf{z}$。合理假设（指定）$p(z)$ 和 $p(x|z)$的分布形式，可以用期望最大化算法（EM）解决。

随机初始化 $\theta_{old}$
E-step：计算 $p_{\theta_{old}} (z|x)$
M-step：计算 $\theta_{new}$，给定：

$$\theta_{new} = argmax_\theta Q(\theta, \theta_{old})$$
其中，
$$Q(\theta, \theta_{old}) = \int_zp_{\theta_{old}}(z|x)\log(p_\theta(x, z))dz$$

EM 比较直观的应用是解决高斯混合模型（Gaussian Mixtrue Model，GMM）的参数估计及K-Means 聚类。更复杂的，语音识别的核心——GMM-HMM 模型的训练也是利用 EM 算法[5]。

这里我们直接给出 ME 算法而省略了最重要的证明，但 EM 是变分推理的基础，如果不熟悉建议先参见 [4] Chapter 9 或 [9]。

3. 4 MCMC

EM 算法中涉及到对 $p(z|x)$ （即隐变量的后验分布）的积分（或求各）。虽然上面举的例子可以方便的通过 EM 算法求解，但由于概率分布的多样性及变量的高维等问题，这个积分一般是难以计算的（intractable）。

因此，可以采用数值积分的方式近似求得 M-step 的积分项。

$$Q(\theta, \theta_{old}) = \int_zp_{\theta_{old}}(z|x)\log(p_\theta(x, z))dz \approx\frac{1}{N}\sum_{i=1}^N\log p_\theta(x, z^i)$$

这涉及到按照 $p(z|x)$ 对 $z$ 进行采样。这需要用到 MCMC 等采样技术。关于 MCMC，LDA数学八卦 0.4.3 讲得非常明白，这里不再赘述。也可以参考 [4] Chapter 11。

3.5 变分推理（Variational Inference，VI）

由于 MCMC 算法的复杂性（对每个数据点都要进行大量采），在大数据下情况，可能很难得到应用。因此，对于

$$p(z|x)$$ 的积分，还需要其他的近似解决方案。

变分推理的思想是，寻找一个容易处理的分布 $q(z)$，使得 $q(z)$ 与目标分布$p(z|x)$ 尽量接近。然后，用$q(z)$ 代替 $p(z|x)$

分布之间的度量采用 Kullback–Leibler divergence（KL 散度），其定义如下：

$KL(q||p) = \int q(t)\log \frac{q(t)}{p(t)}dt=E_q(\log q-\log p)=E_q(\log q)-E_q[\log p]$

在不致引起歧义的情况下，我们省略 $E$ 的下标。这里不加证明的指出 KL 的一些重要性质：$KL(q||p) \ge 0$ 且 $KL(q||p) = 0 \iff q =p$ [6]

注：KL散度不是距离度量，不满足对称性和三角不等式

因此，我们寻找 $q(\mathbf{z})$ 的问题，转化为一个优化问题：

$$q^*(z) = argmax_{q(z) \in Q}KL(q(z)||p(z|x))$$

$KL(q(z)||p(z|x))$ 是关于 $q(z)$ 函数，而 $q(z) \in Q$ 是一个函数，因此，这是一个泛函（函数的函数）。而变分（variation）求极值之于泛函，正如微分求极值之于函数。
如果对于变分的说法一时不好理解，可以简单地将变分视为高斯分布中的高斯、傅里叶变换中的傅里叶一样的专有名词，不要尝试从字面去理解。
另外不要把变分（variation）与 variable（变量）, variant（方差）等混淆，它们之间没有关系。

ELBO（Evidence Lower Bound Objective）

根据 KL 的定义及 $p(z|x) = \frac{p(z, x)}{p(x)}$

$$KL(q(z)||p(z|x)) = E[\log q(z)] -E[\log p(z, x)] + \log p(x)$$

令

$$ELBO(q) = E[\log p(z, x)] - E[\log q(z)]$$
根据 KL 的非负性质，我们有
$$\log p(x) = KL(q(x)||p(z|x)) + ELBO(q) \ge ELBO(q)$$

ELBO 是 $p(x)$ 对数似似然（即证据，evidence）的一个下限（lower bound）。

对于给定的数据集，$p(x)$ 为常数，由

$$KL(q(x)||p(z|x)) = \log p(x) - ELBO(q)$$
最小化 KL 等价于最大化 ELBO 。

关于变分推理这里就简单介绍这么多。有兴趣的话可以参考 [6]、[4] Chapter 10 以及最新的 tutorial [10]。

3.6 VAE

这里主要是按照 [1] 的思路来讨论 VAE。

观测数据 $x^{(i)}$ 的对数似然可以写作：

$$\log p_\theta(x^{(i)} = KL(q_\varPhi(z|x^{(i)})||p_\theta(z|x^{(i)})) + L(\theta, \varPhi; x^{(i)}))$$

这里我们将 $ELBO$ 记作 L，以强调需要优化的参数。
我们可以通过优化 L，来间接的优化似然。

VI 中我们通过优化 L 来优化 KL。

根据概率的乘法公式，经过简单的变换，L 可以写作

$$L(\theta, \varPhi; x^{(i)})) = -KL(q_\varPhi(z|x^{(i)})||p_\theta(z)) + E_{q_\varPhi(z|x)}[\log p_\theta(x^{(i)}|z)]$$

因此，我们优化的目标可以分解成等号右边的两项。

3.6.1 第一项

我们先考察第一项，这是一个 KL 散度。$q$ 是我们要学习的分布，$p$ 是隐变量的先验分布。通过合理的选择分布形式，这一项可以解析的求出。

如果，$q$ 取各维独立的高斯分布（即第1部分的 decoder），同时令 $p$ 是标准正态分布，那么，可以计算出，两者之间的 KL 散度为：

$$-KL(q_\varPhi(z|x^{(i)})||p_\theta(z)) = -0.5 * (1+\log\sigma^2_i-\mu^2_i -\sigma^2_i)=-0.5(1+\log\sigma^2_i-\mu^2_i-exp(\log\sigma^2_i))$$

这就是本文第1部分目标函数的 KL 项了。

具体证明见 [1] 附录B。

3.6.2 第二项

然后，我们考察等式右边第二项。$E_{q_\varPhi(z|x)}[\log p_\theta(x^{(i)}|z)]$ 是关于 $x^{(i)}$ 的后验概率的对数似然。

由于 VAE 并不对 $q(z|x)$ （decoder） 做太强的假设（我们的例子中，是一个神经网络），因引，这一项不能解析的求出。所以我们考虑采样的方式。

$$E_{q_\varPhi(z|x)}[\log p_\theta(x^{(i)}|z)] \approx \frac{1}{L}\sum_{j=1}^L\log p_\theta(x^{(i)}|z^{(j)})$$
这里 $z^{(j)}$ 不是通过从 decoder 建模的高斯分布直接采样，而是使用了第1部分介绍的 reparameterization 方法，其正确性证明见[1]的2.3小节。

如果每次只采一个样本点，则

$$E_{q_\varPhi(z|x)}[\log p_\theta(x^{(i)}|z)] \approx \log p_\theta(x^{(i)}|\tilde{z})$$

其中，$\tilde{z}$ 为采样点。很幸运，这个式正是神经网络常用的损失函数。

3.6.3 损失函数

通过上面讨论，VAE 的优化目标都成为了我们熟悉并容易处理的形式。下面，我们针对 $p_\theta(x^{(i)}|\tilde{z})$（encoder）的具体建模分布，推导下神经网络训练中实际的损失函数。

第1部分介绍了 交叉熵和均方误差两种损失函数。下面简单介绍下，两种损失对应的不同概率分布假设。以下分布均假设 $x$ 的各维独立。

交叉熵

如果假设 $p(x_i|z), (i = 1,.., n)$ 服从伯努力分布，即：

$$p(x=1|z) = \alpha_z, p(x=0) = 1- \alpha_z$$
对于某个观测值，其似然为：
$$L = \alpha_z^x \cdot (1-\alpha_z)^{1-x}$$

decoder 输出为伯努力分布的参数，即 $\alpha_z = decoder(z) = \hat{x}$。则对数似然为：

$$\log L = x \cdot log(\hat{x}) + (1-x) \log(1-\hat{x})$$
$-\log L$ 这就是我们使用的交叉熵。

均方误差

如果假设

$$p(x_i|z), (i = 1,.., n)$$ 服务高斯分布，即
$$p(x|z)=\frac{1}{\sqrt{2\pi}\sigma} \cdot e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$

对数似然为：

$$\log L = -0.5*\log(2\pi) -0.5*\log \sigma-\frac{(x-\mu)^2}{2\sigma^2}$$

decoder 为高斯分布的期望，这里不关心方差，即$\sigma$为未知常数。我们是优化目标为（去掉与优化无关的常数项）：

$$\max -\frac{(x-\mu)^2}{2\sigma^2} = \min (x-\mu)^2$$
这就是我们要优化的均方误差。

对不同损失函数与概率分布的联系，详细讨论见 [4] Chapter 5。

4. 结语

对这个领域的接触不多，认识浅显，文献也读的少，更多的是一些疑问：

• VAE 是非常漂亮的工作，是理论指导模型结构设计的范例。

• [1] [2] 独立提出 VAE。虽然最后提出的算法大致相同，但出发点和推导思路还是有明显不同，应该放在一起相互参照。

• VAE 作为一种特征学习方法，与同样是非监督的 AE、 RBM 等方法相比，优劣势分是什么？

• [2] 讨论了与 denoising AE 的关系，但 VAE 在形式上与 constractive auto-encoder 更相似，不知道两者的关系如何理解。

• 有些工作利用 VAE 作半监督学习，粗略看了些，并没有展现出相比于其他预训练方法的优势[3, 12]。

• 结合上面几点，虽然 VAE 是一个很好的工具，新的“论文增长点”，但仅就深度学习而言，感觉仅仅只是另一种新的工具。

---

Refences

1. Kingma et al. Auto-Encoding Variational Bayes.
2. Rezende et al. Stochastic Backpropagation and Approximate Inference in Deep Generative Models.
3. Kingma and Rezende et al. Semi-supervised Learning with Deep Generative Models.
4. Bishop. Pattern Recognition and Machine Learning.
5. Young et al. HTK handbook.
6. Blei et al. Variational Inference: A Review for Statisticians.
7. Doersch. Tutorial on Variational Autoencoders.
8. Kevin Frans. Variational Autoencoders Explained.
9. Sridharan. Gaussian mixture models and the EM algorithm.
10. Blei et al. Variational Inference: Foundations and Modern Methods.
11. Durr. Introduction to variational autoencoders .
12. Xu et al. Variational Autoencoders for Semi-supervised Text Classification.