标签:turn 计算 data 字母 line ref img get 练习
小Hi平时的一大兴趣爱好就是演奏钢琴。我们知道一个音乐旋律被表示为长度为 N 的数构成的数列。
小Hi在练习过很多曲子以后发现很多作品自身包含一样的旋律。旋律是一段连续的数列,相似的旋律在原数列可重叠。比如在1 2 3 2 3 2 1 中 2 3 2 出现了两次。
小Hi想知道一段旋律中出现次数至少为K次的旋律最长是多少?
第一行两个整数 N和K。1≤N≤20000 1≤K≤N
接下来有 N 个整数,表示每个音的数字。1≤数字≤100
一行一个整数,表示答案。
8 2 1 2 3 2 3 2 3 1
4
先求出后缀数组,问题转换为询问height数组中连续k-1个数的最小值的最大值,单调队列扫描一遍即可。
1 #include <cstdio> 2 #include <cstring> 3 #include <cstdlib> 4 5 #define siz 1024 6 7 inline int get_c(void) 8 { 9 static char buf[siz]; 10 static char *head = buf + siz; 11 static char *tail = buf + siz; 12 13 if (head == tail) 14 fread(head = buf, 1, siz, stdin); 15 16 return *head++; 17 } 18 19 inline int get_i(void) 20 { 21 register int ret = 0; 22 register int neg = false; 23 register int bit = get_c(); 24 25 for (; bit < 48; bit = get_c()) 26 if (bit == ‘-‘)neg ^= 1; 27 28 for (; bit > 47; bit = get_c()) 29 ret = ret * 10 + bit - 48; 30 31 return neg ? -ret : ret; 32 } 33 34 #define N 20005 35 36 int n, m, s[N]; 37 int A[N], cntA[N]; 38 int B[N], cntB[N]; 39 int sa[N], rk[N], ht[N], tsa[N]; 40 int que[N], hd, tl, answer; 41 42 signed main(void) 43 { 44 n = get_i(); 45 m = get_i(); 46 47 for (int i = 1; i <= n; ++i) 48 s[i] = get_i(); 49 50 memset(cntA, 0, sizeof(cntA)); 51 52 for (int i = 1; i <= n; ++i) 53 ++cntA[s[i]]; 54 55 for (int i = 1; i <= 100; ++i) 56 cntA[i] += cntA[i - 1]; 57 58 for (int i = n; i >= 1; --i) 59 sa[cntA[s[i]]--] = i; 60 61 rk[sa[1]] = 1; 62 63 for (int i = 2; i <= n; ++i) 64 rk[sa[i]] = rk[sa[i - 1]] + (s[sa[i]] != s[sa[i - 1]]); 65 66 for (int l = 1; rk[sa[n]] < n; l <<= 1) 67 { 68 memset(cntA, 0, sizeof(cntA)); 69 memset(cntB, 0, sizeof(cntB)); 70 71 for (int i = 1; i <= n; ++i) 72 { 73 ++cntA[A[i] = rk[i]]; 74 ++cntB[B[i] = i + l <= n ? rk[i + l] : 0]; 75 } 76 77 for (int i = 1; i <= n; ++i) 78 cntB[i] += cntB[i - 1]; 79 80 for (int i = 1; i <= n; ++i) 81 cntA[i] += cntA[i - 1]; 82 83 for (int i = n; i >= 1; --i) 84 tsa[cntB[B[i]]--] = i; 85 86 for (int i = n; i >= 1; --i) 87 sa[cntA[A[tsa[i]]]--] = tsa[i]; 88 89 rk[sa[1]] = 1; 90 91 for (int i = 2; i <= n; ++i) 92 rk[sa[i]] = rk[sa[i - 1]] + (A[sa[i]] != A[sa[i - 1]] || B[sa[i]] != B[sa[i - 1]]); 93 } 94 95 for (int i = 1, j = 0; i <= n; ++i) 96 { 97 j = j ? j - 1 : 0; 98 while (s[i + j] == s[sa[rk[i] - 1] + j])++j; 99 ht[rk[i]] = j; 100 } 101 102 for (int i = 1; i < m; ++i) 103 { 104 while (tl != hd && ht[i] < ht[que[tl]]) 105 --tl; 106 que[++tl] = i; 107 } 108 109 answer = ht[que[hd]]; 110 111 for (int i = m; i <= n; ++i) 112 { 113 while (tl != hd && ht[i] < ht[que[tl]]) 114 --tl; 115 116 que[++tl] = i; 117 118 while (hd != tl && que[hd + 1] <= i - m + 1) 119 ++hd; 120 121 if (answer < ht[que[hd + 1]]) 122 answer = ht[que[hd + 1]]; 123 } 124 125 printf("%d\n", answer); 126 }
小Hi平时的一大兴趣爱好就是演奏钢琴。我们知道一个音乐旋律被表示为长度为 N 的数构成的数列。小Hi在练习过很多曲子以后发现很多作品自身包含一样的旋律。
旋律可以表示为一段连续的数列,相似的旋律在原数列不可重叠,比如在1 2 3 2 3 2 1 中 2 3 2 出现了一次,2 3 出现了两次,小Hi想知道一段旋律中出现次数至少为两次的旋律最长是多少?
第一行一个整数 N。1≤N≤100000
接下来有 N 个整数,表示每个音的数字。1≤数字≤1000
一行一个整数,表示答案。
8 1 2 3 2 3 2 3 1
2
二分答案,转换为判断是否存在长度>=k的不重叠的两个子串。判定两个后缀是否重叠,只需要看abs(st1-st2)和k的大小关系即可,所以找出极长的连续的大于等于k的一段height,维护其中的st的最大和最小值,即可判断是否存在合法的两个子串。
1 #include <bits/stdc++.h> 2 3 #define siz 1024 4 5 inline int get_c(void) 6 { 7 static char buf[siz]; 8 static char *head = buf + siz; 9 static char *tail = buf + siz; 10 11 if (head == tail) 12 fread(head = buf, 1, siz, stdin); 13 14 return *head++; 15 } 16 17 inline int get_i(void) 18 { 19 register int ret = 0; 20 register int neg = false; 21 register int bit = get_c(); 22 23 for (; bit < 48; bit = get_c()) 24 if (bit == ‘-‘)neg ^= true; 25 26 for (; bit > 47; bit = get_c()) 27 ret = ret * 10 + bit - 48; 28 29 return neg ? -ret : ret; 30 } 31 32 #define N 100005 33 34 const int inf = 2e9 + 7; 35 36 int n, s[N]; 37 int A[N], cntA[N]; 38 int B[N], cntB[N]; 39 int sa[N], rk[N], ht[N], ta[N]; 40 41 inline bool check(int k) 42 { 43 int max = sa[1], min = sa[1]; 44 45 for (int i = 2; i <= n; ++i) 46 { 47 if (ht[i] >= k) 48 { 49 if (max < sa[i]) 50 max = sa[i]; 51 if (min > sa[i]) 52 min = sa[i]; 53 if (min + k <= max) 54 return true; 55 } 56 else 57 max = min = sa[i]; 58 } 59 60 return false; 61 } 62 63 signed main(void) 64 { 65 n = get_i(); 66 67 for (int i = 1; i <= n; ++i) 68 s[i] = get_i(); 69 70 memset(cntA, 0, sizeof(cntA)); 71 72 for (int i = 1; i <= n; ++i) 73 ++cntA[s[i]]; 74 75 for (int i = 1; i <= 1000; ++i) 76 cntA[i] += cntA[i - 1]; 77 78 for (int i = n; i >= 1; --i) 79 sa[cntA[s[i]]--] = i; 80 81 rk[sa[1]] = 1; 82 83 for (int i = 2; i <= n; ++i) 84 rk[sa[i]] = rk[sa[i - 1]] + (s[sa[i]] != s[sa[i - 1]]); 85 86 for (int l = 1; rk[sa[n]] < n; l <<= 1) 87 { 88 memset(cntA, 0, sizeof(cntA)); 89 memset(cntB, 0, sizeof(cntB)); 90 91 for (int i = 1; i <= n; ++i) 92 { 93 ++cntA[A[i] = rk[i]]; 94 ++cntB[B[i] = i + l <= n ? rk[i + l] : 0]; 95 } 96 97 for (int i = 1; i <= n; ++i) 98 cntA[i] += cntA[i - 1]; 99 for (int i = 1; i <= n; ++i) 100 cntB[i] += cntB[i - 1]; 101 102 for (int i = n; i >= 1; --i) 103 ta[cntB[B[i]]--] = i; 104 105 for (int i = n; i >= 1; --i) 106 sa[cntA[A[ta[i]]]--] = ta[i]; 107 108 rk[sa[1]] = 1; 109 110 for (int i = 2; i <= n; ++i) 111 rk[sa[i]] = rk[sa[i - 1]] + (A[sa[i]] != A[sa[i - 1]] || B[sa[i]] != B[sa[i - 1]]); 112 } 113 114 for (int i = 1, j = 0; i <= n; ++i) 115 { 116 if (--j < 0)j = 0; 117 while (s[i + j] == s[sa[rk[i] - 1] + j])++j; 118 ht[rk[i]] = j; 119 } 120 121 int lt = 1, rt = n, mid, ans = 0; 122 123 while (lt <= rt) 124 { 125 mid = (lt + rt) >> 1; 126 if (check(mid)) 127 ans = mid, lt = mid + 1; 128 else 129 rt = mid - 1; 130 } 131 132 printf("%d\n", ans); 133 }
小Hi平时的一大兴趣爱好就是演奏钢琴。我们知道一个音乐旋律被表示为长度为 N 的数构成的数列。小Hi在练习过很多曲子以后发现很多作品中的旋律有共同的部分。
旋律是一段连续的数列,如果同一段旋律在作品A和作品B中同时出现过,这段旋律就是A和B共同的部分,比如在abab 在 bababab 和 cabacababc 中都出现过。小Hi想知道两部作品的共同旋律最长是多少?
共两行。一行一个仅包含小写字母的字符串。字符串长度不超过 100000。
一行一个整数,表示答案。
abcdefg abacabca
3
把两个串接在一起跑后缀数组,找出最大的height使得两个后缀从不同串开始即可。
1 #include <bits/stdc++.h> 2 3 #define N 200005 4 5 int n; 6 int m; 7 int len; 8 int cut; 9 int s[N]; 10 int sa[N]; 11 int rk[N]; 12 int ta[N]; 13 int ht[N]; 14 int A[N], cntA[N]; 15 int B[N], cntB[N]; 16 17 char s1[N]; 18 char s2[N]; 19 20 signed main(void) 21 { 22 scanf("%s", s1 + 1); 23 scanf("%s", s2 + 1); 24 25 n = strlen(s1 + 1); 26 m = strlen(s2 + 1); 27 28 for (int i = 1; i <= n; ++i) 29 s[++len] = s1[i] - ‘a‘ + 1; 30 31 s[cut = ++len] = 0; 32 33 for (int i = 1; i <= m; ++i) 34 s[++len] = s2[i] - ‘a‘ + 1; 35 36 s[++len] = 27; 37 38 memset(cntA, 0, sizeof(cntA)); 39 40 for (int i = 1; i <= len; ++i) 41 ++cntA[s[i]]; 42 43 for (int i = 1; i <= 30; ++i) 44 cntA[i] += cntA[i - 1]; 45 46 for (int i = len; i >= 1; --i) 47 sa[cntA[s[i]]--] = i; 48 49 rk[sa[1]] = 1; 50 51 for (int i = 2; i <= len; ++i) 52 rk[sa[i]] = rk[sa[i - 1]] + (s[sa[i]] != s[sa[i - 1]]); 53 54 for (int l = 1; rk[sa[len]] < len; l <<= 1) 55 { 56 memset(cntA, 0, sizeof(cntA)); 57 memset(cntB, 0, sizeof(cntB)); 58 59 for (int i = 1; i <= len; ++i) 60 { 61 ++cntA[A[i] = rk[i]]; 62 ++cntB[B[i] = i + l <= len ? rk[i + l] : 0]; 63 } 64 65 for (int i = 1; i <= len; ++i) 66 cntA[i] += cntA[i - 1], 67 cntB[i] += cntB[i - 1]; 68 69 for (int i = len; i >= 1; --i) 70 ta[cntB[B[i]]--] = i; 71 72 for (int i = len; i >= 1; --i) 73 sa[cntA[A[ta[i]]]--] = ta[i]; 74 75 rk[sa[1]] = 1; 76 77 for (int i = 2; i <= len; ++i) 78 rk[sa[i]] = rk[sa[i - 1]] + ( 79 A[sa[i]] != A[sa[i - 1]] 80 || B[sa[i]] != B[sa[i - 1]]); 81 } 82 83 for (int i = 1, j = 0; i <= len; ++i) 84 { 85 if (--j < 0)j = 0; 86 while (s[i + j] == s[sa[rk[i] - 1] + j])++j; 87 ht[rk[i]] = j; 88 } 89 90 int ans = 0; 91 92 for (int i = 2; i <= len; ++i) 93 if ((sa[i] < cut) != (sa[i - 1] < cut)) 94 ans = std::max(ans, ht[i]); 95 96 printf("%d\n", ans); 97 }
小Hi平时的一大兴趣爱好就是演奏钢琴。我们知道一个音乐旋律被表示为长度为 N 的数构成的数列。小Hi在练习过很多曲子以后发现很多作品中的旋律有重复的部分。
我们把一段旋律称为(k,l)-重复的,如果它满足由一个长度为l的字符串重复了k次组成。 如旋律abaabaabaaba是(4,3)重复的,因为它由aba重复4次组成。
小Hi想知道一部作品中k最大的(k,l)-重复旋律。
一行一个仅包含小写字母的字符串。字符串长度不超过 100000。
一行一个整数,表示答案k。
babbabaabaabaabab
4
这道题有点复杂…… 好在HiHo的提示很好。
小Ho:这一次的问题该如何解决呢?
小Hi:嗯,这次的问题是重复次数最多的连续字串。
小Ho:似乎不好下手啊。
小Hi:那我们先降低难度,不如考虑如何解决如何求一个串的最大重复次数。
小Ho:嗯。我想想,比如说串abababab,既可以是(1,8),也可以是(2,4),最大的是(4,2)。
小Hi:对。假如说我们枚举一个可能的循环节长度l(或者k),能不能快速判断这个l是否合法呢?
小Ho:啊!我想想...似乎是求原串和原串去掉前l个字符后两个串的LCP(最长公共前缀),如果能完全匹配上,就满足!
小Hi:对,没错。比如abababab,检验是否是(2,4),就拿abababab和ababab求LCP。
小Hi:值得一提的是,利用height数组可以快速求出我们需要的LCP。例如abababab的height数组如下:
| suffix | sa | height |
|---|---|---|
| ab | 7 | 0 |
| abab | 5 | 2 |
| ababab | 3 | 4 |
| abababab | 1 | 6 |
| b | 8 | 0 |
| bab | 6 | 1 |
| babab | 4 | 3 |
| bababab | 2 | 5 |
小Hi:如果我们要求某两个后缀的LCP,只要求它们中间的一段height数组的最小值即可。例如abababab和ababab的LCP就是[4]这段的最小值,即2;bab和bababab的LCP就是[3, 5]这段的最小值,即3;ab和babab的LCP就是[2, 4, 6, 0, 1, 3]这段的最小值,即0。
小Hi:这个求height数组某一段最小值的问题,恰好是之前讲过的[RMQ问题],可以通过O(NlogN)的预处理达到O(1),处理单次询问;当然使用线段树等数据结构也是可以的,单次询问O(logN)。
小Ho:明白了。回到原问题,那我们肯定是要先枚举(k,l)中的这个l,再枚举起始位置i,计算Suffix(i)和Suffix(i+l)的LCP,记作lcp(l, i),那么k(l, i)就等于lcp(l,i)/l + 1。对于所有的循环节长度l和起始位置i,最大的k(l, i)就是答案。
小Hi:你说的对!不过本题还是有进一步优化的空间。对于确定的l,我们不用枚举所有的起始位置i,而只枚举i是l的整数倍的情况。如果最优串的开始位置恰好在l的倍数上,那我们找到的最大的k就是正确答案。
小Ho:道理是这么个道理。不过如果最优串的开始位置不在l的倍数上呢?
小Hi:即使不是,问题也会太糟糕,假如说最优串位置在x,可以想象我们会枚举到x之后的一个最近位置p,p是l的倍数。并且我们计算出了Suffix(p)和Suffix(p+l)的LCP,lcp(l, p)那么此时的k(l, p)=lcp(l, p)/l+1。
小Hi:对于被我们略过的k(l, p-1), k(l, p-2) ... k(l, p-l+1),它们的上限是k(l, p)+1。
小Ho:没错。因为它们的起始位置距离p不超过l,所以最多比Suffix(p)增加一个循环节。
小Hi:其次,如果k(l, p-1), k(l, p-2) ... k(l, p-l+1)中有一个的值是k(l, p)+1的话,那么k(l, p - l + lcp(l, p) mod l)一定等于k(l, p)+1。(mod是取余运算)
小HO:为什么呢?
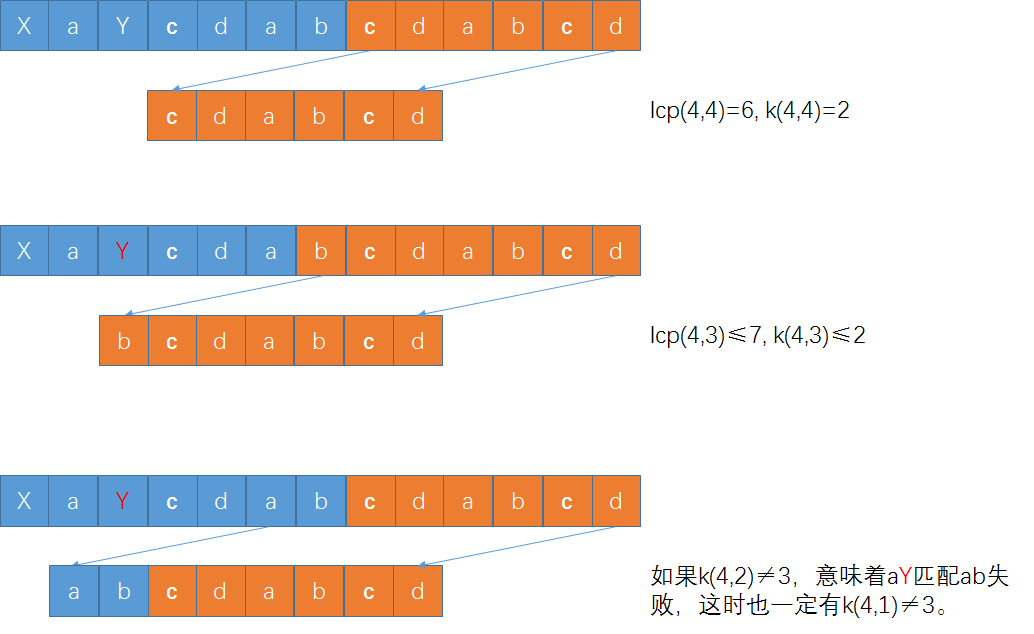
小Hi:举个例子,比如串XaYcdabcdabcd(XY各代表一个不确定的字符,具体代表的字符会影响最后答案,我们后面会分析到),当我们考虑l=4的时候,第一次枚举p=4的起始位置,会求出cdabcdabcd和cdabcd的lcp(4, 4)=6,k(4, 4)=2。根据上面的论断,只有当k(l, p - l + lcp(l, p) mod l)=k(4, 4 - 4 + 6 mod 4)=k(4, 2)=3时,k(4, 1), k(4, 2)和k(4, 3)中才会有3。首先我们可以判断k(4, 3)一定不可能等于3,因为无论Y是哪个字符,Ycdabcdabcd和bcdabcd的LCP即lcp(4, 3)最大是7,不到8。 其次如果k(4, 2) ≠ 3,那么k(4, 1)也没戏。因为如果k(4, 2) ≠ 3,说明aY和ab匹配不上,这时无论X是哪个字符,XaY和dab匹配不上,lcp(4, 1) < l,k(4, 1) = 1。
小Ho:哦,我有点明白了。k(l, p - l + lcp(l, p) mod l)是一个分界线,右边的值因为LCP不够大,一定不能增加一个循环节。并且如果k(l, p - l + lcp(l, p) mod l)没有增加循环节的话,说明[p - l + lcp(l, p) mod l, p]这段中间匹配出错,左边的lcp也跟着雪崩,更不可能增加循环节了。
小Hi:没错!
小Ho:那枚举l和枚举开始位置的时间复杂度呢?
小Hi:你会发现,枚举完l后枚举开始位置的时间复杂度是O(n/l)的,所以总复杂度是O(n/1)+O(n/2)+O(n/3)...这个是一个经典的求和,总复杂度是O(nlogn)的。
小Ho:明白了!好神奇,看似简单朴素的想法,复杂度却也很低。
小Hi:是啊。以下是二分判断的C++代码实现:
for(L=1;L <= n;L++)
{
for (int i = 1; i + L <= n; i += L)
{
int R = lcp(i, i + L);
ans = max(ans, R / L + 1);
if (i >= L - R % L)
{
ans = max(lcp(i - L + R%L, i + R%L) / L + 1, ans);
}
}
}
小Ho:好的。我这就实现一下。
然后我就实现了一下…… 对于证明一脸懵逼……
1 #include <bits/stdc++.h> 2 3 #define N 100005 4 5 int n; char s[N]; 6 7 int A[N], cntA[N]; 8 int B[N], cntB[N]; 9 int sa[N], rk[N], ht[N], ta[N]; 10 11 int tr[N << 2]; 12 13 void build(int t, int l, int r) 14 { 15 if (l == r) 16 tr[t] = ht[l]; 17 else 18 { 19 int mid = (l + r) >> 1; 20 build(t << 1, l, mid); 21 build(t << 1 | 1, mid + 1, r); 22 tr[t] = std::min( 23 tr[t << 1], 24 tr[t << 1 | 1] 25 ); 26 } 27 } 28 29 int query(int t, int l, int r, int a, int b) 30 { 31 if (l == a && r == b) 32 return tr[t]; 33 int mid = (l + r) >> 1; 34 if (b <= mid) 35 return query(t << 1, l, mid, a, b); 36 else if (a > mid) 37 return query(t << 1 | 1, mid + 1, r, a, b); 38 else 39 return std::min( 40 query(t << 1, l, mid, a, mid), 41 query(t << 1 | 1, mid + 1, r, mid + 1, b) 42 ); 43 } 44 45 inline int lcp(int a, int b) 46 { 47 a = rk[a]; 48 b = rk[b]; 49 50 if (a > b) 51 std::swap(a, b); 52 53 return query(1, 1, n, a + 1, b); 54 } 55 56 signed main(void) 57 { 58 scanf("%s", s + 1); n = strlen(s + 1); 59 60 memset(cntA, 0, sizeof(cntA)); 61 62 for (int i = 1; i <= n; ++i) 63 ++cntA[s[i]]; 64 65 for (int i = 1; i <= 300; ++i) 66 cntA[i] += cntA[i - 1]; 67 68 for (int i = n; i >= 1; --i) 69 sa[cntA[s[i]]--] = i; 70 71 rk[sa[1]] = 1; 72 73 for (int i = 2; i <= n; ++i) 74 rk[sa[i]] = rk[sa[i - 1]] + (s[sa[i]] != s[sa[i - 1]]); 75 76 for (int l = 1; rk[sa[n]] < n; l <<= 1) 77 { 78 memset(cntA, 0, sizeof(cntA)); 79 memset(cntB, 0, sizeof(cntB)); 80 81 for (int i = 1; i <= n; ++i) 82 { 83 ++cntA[A[i] = rk[i]]; 84 ++cntB[B[i] = i + l <= n ? rk[i + l] : 0]; 85 } 86 87 for (int i = 1; i <= n; ++i) 88 cntA[i] += cntA[i - 1], 89 cntB[i] += cntB[i - 1]; 90 91 for (int i = n; i >= 1; --i) 92 ta[cntB[B[i]]--] = i; 93 94 for (int i = n; i >= 1; --i) 95 sa[cntA[A[ta[i]]]--] = ta[i]; 96 97 rk[sa[1]] = 1; 98 99 for (int i = 2; i <= n; ++i) 100 rk[sa[i]] = rk[sa[i - 1]] + (A[sa[i]] != A[sa[i - 1]] || B[sa[i]] != B[sa[i - 1]]); 101 } 102 103 for (int i = 1, j = 0; i <= n; ++i) 104 { 105 if (--j < 0)j = 0; 106 while (s[i + j] == s[sa[rk[i] - 1] + j])++j; 107 ht[rk[i]] = j; 108 } 109 110 build(1, 1, n); 111 112 int ans = 0; 113 114 for (int L = 1; L <= n; ++L) 115 { 116 for (int i = 1; i + L <= n; i += L) 117 { 118 int R = lcp(i, i + L); 119 ans = std::max(ans, R/L + 1); 120 if (i >= L - R % L) 121 ans = std::max(ans, 122 lcp(i-L+R%L,i+R%L)/L+1); 123 } 124 } 125 126 printf("%d\n", ans); 127 }
@Author: YouSiki
标签:turn 计算 data 字母 line ref img get 练习
原文地址:http://www.cnblogs.com/yousiki/p/6206262.html