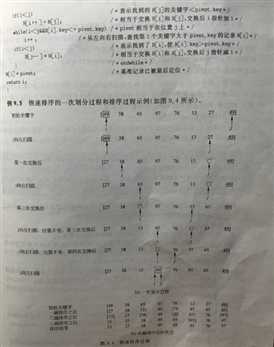
将被排序的记录数组R[1...n]垂直排序,每个记录R[i]看做是重量为R[i].key的气泡。根据轻气泡不能再重气泡之下的原则,从下往上的原则,从下往上(也可以从上往下)扫描数组R,一旦扫描到违反此原则的轻气泡,就使其向上“漂浮”。如此反复进行,直到最后任何两个气泡都是轻者在上、重者在下为止。
快速排序
1.基本思想
设当前待排序的无序区为R[low...high]
【1】分解
在R[low...high]中任选一个记录作为基准(Pivot),以此基准将当前无序区划分为左、右两个较小的子区间R[low...pivotpos-1]和R[pivotpos+1...high],并使左边子区间中所有记录的关键字均小于等于基准记录(不妨记为pivot, pivot=R[pivotpos])的关键字pivot.key,右边的子区间中所有记录的关键字均大于等于pivot.key,而基准记录pivot则位于正确的位置(pivotpos)上,它无须参加后续的排序。划分的关键是求出基准记录所在的位置pivotpos;划分的结果可以简单地表示为R[low...pivotpos-1].keys <= R[pivotpos].key <= R[pivotpos+1...high].keys ,其中low <= pivotpos <= high.
【2】求解
通过递归调用快速排序对左、右子区间R[low..pivotpos-1]和R[pivotpos+1..high]进行快速排序.
【3】组合
因为当“求解”步骤中的两个递归调用结束时,其左、右两个子区间已有序,所以对快速排序而言,“组合”步骤无须做什么,可看做是空操作.
划分算法
第一步:(初始化)设置两个指针i和j,它们的初值分别为区间的下界和上界,即i=low,j=high;选取无序区的第一个记录R[i](R[low])作为基准记录,并将它保存在变量pivot中。
第二步:令j自high起向左扫描,直到找到第1个关键字小于pivot.key的记录R[j],将R[j]移至i所指的位置上,这相当于R[j]和基准R[i](pivot)进行了交换,使关键字小于基准关键字pivot.key的记录移到了基准的左边,交换后R[j]中相当于是pivot;然后,令i指针自i+1位置开始向右扫描,直至找到第1个关键字大于pivot.key的记录R[i],将R[i]移到i所指的位置上,这相当于交换了R[i]和基准R[j],使关键字大于基准关键字的记录移到了基准的右边,交换后R[i]中又相当于存放了pivot;接着令指针j自位置j-1开始向左扫描,如此交替改变扫描方向,从两端各自往中间靠拢,直至i=j时,i便是基准pivot最终的位置,将pivot放在此位置上就完成了一次划分。
2.算法分析
(1)O(n^2) =< 时间复杂度 =< O(nlog2^n),平均时间复杂度为O(nlog2^n)
(2)快速排序在系统内部需要一个栈来实现递归。若每次划分较为均匀,则其递归树的高度为O(nlog2^n),故递归后需栈空间为O(nlog2^n)。最坏情况下,递归树的高度为 O(n),所需的栈空间为 O(n)【栈空间即为时间复杂度】
(4)基准关键字的选取,在当前无序区中选取划分的基准关键字是决定算法性能的关键。
【1】“三者取中”规则,即在当前区间里,将该区间首尾和中间位置上的关键字进行比较,取三者之中值所对应的记录作为基准,在划分开始前将该基准记录和该区间的第1个记录进行交换,此后的划分过程与上面所给的划分算法完全相同。
【2】取位于low和high之间的随机数k(low <= k <= high),用R[k]作为基准。选取基准最好的方法是用一个随机函数产生一个取位于low和high之间的随机数k(low <= k <= high)用R[k]作为基准,这相当于强迫R[low...high]中的记录是随机分布的。用此方法所得到的快速排序一般称为随机的快速排序.
分治法
基本思想:将原问题分解为若干个规模更小但结构与原问题相似的子问题,递归地解这些子问题,然后将这些子问题的解组合为原问题的解。