标签:current model sid res 数据集 决策 plot 准则 otl
(上接第三章)
3.4 Scikit-Learn与回归树
3.4.1 回归算法原理
在预测中,CART使用最小剩余方差(squared Residuals Minimization)来判断回归时的最优划分,这个准则期望划分之后的子树与样本点的误差方差最小。这样决策树将数据集切分成很多子模型数据,然后利用线性回归技术来建模。如果每次切分后的数据子集仍难以拟合,就继续切分。在这种切分方式下创建的预测树,每个子节点都是一个线性回归模型。因此,CART不仅支持整体预测,也支持局部模式的预测,并有能力从整体中找到模式,或根据模式组合成一个整体
CART的算法流程:
(1)决策树主函数:决策树的主函数是一个递归的函数。该函数的主要功能是按照CART的规则生长出决策树的各个分支节点,并根据终止条件结束算法:
1)输入需要分类的数据集合类别标签
2)使用最小剩余方差判定回归树的最优划分,并创建特征的划分节点—最小剩余方差子函数。
3)在划分节点划分数据集为两部分—二分数据集子函数
4)根据二分数据的结果构建出新的左、右节点,作为树生长出来的两个分支
5)检验是否符合递归的终止条件
6)将划分的新节点包含的数据集和类别标签作为输入,递归执行上述步骤。
(2)使用最小剩余方差子函数,计算数据集各列的最优划分方差、划分列、划分值。
(3)二分数据集:根据给定的分割列和分割值将数据集一分为二,分别返回。
#coding:utf-8 #二元切分数据集 #dataSet:输入的数据集;feature:特征列;value:二分点的取值 def binSplit(dataSet,feature,value): #数据集feature列大于value的所有行向量 mat0 = dataSet[nonzero(dataSet[:,feature]>value)[0],:][0] #数据集feature列小于等于value的所有行向量 mat1 = dataSet[nonzero(dataSet[:,feature]<=value)[0],:][0] return mat0,mat1
3.4.2 最小剩余方差法
每次最佳分支特征的选取过程如下:
(1)先令最佳方差为无限大bestVar = inf
(2)依次遍历所有特征列及每个特征列的所有样本点(这是一个二重循环)在每个样本点上二分数据集。
(3)计算二分数据后的总方差currentVar(划分后左、右子数据集的总方差之和),如果currentVar<bestVar,则bestVar=currentVar
(4)返回计算的最优分支特征列、分支特征值(连续特征则为划分点的值),以及左右分支子数据集到主程序。
3.4.3 模型树
3.4.4 剪枝策略
3.4.5 Scikit-Learn实现
import numpy as np from numpy import * from sklearn.tree import DecisionTreeRegressor import matplotlib.pyplot as plt #Scikit-Learn实现 def plotfigure(X,X_test,y,yp): plt.figure() plt.scatter(X,y,c=‘k‘,label=‘data‘) plt.plot(X_test,yp,c=‘r‘,label="max_depth=5",linewidth=2) plt.xlabel("data") plt.ylabel("target") plt.title("Decision Tree Regression") plt.legend() plt.show() x = np.linspace(-5,5,200) siny = np.sin(x) #输出y与x的基本关系 X = mat(x).T y = siny + np.random.rand(1,len(siny))*1.5 #加入噪声的点集 y = y.tolist()[0] #fit regression model clf = DecisionTreeRegressor(max_depth=4) #max depth选取最大的数深度,类似先剪枝 clf.fit(X,y) #Predict X_test = np.arange(-5.0,5.0,0.05)[:,np.newaxis] #添加新的维度 yp = clf.predict(X_test) plotfigure(X,X_test,y,yp)
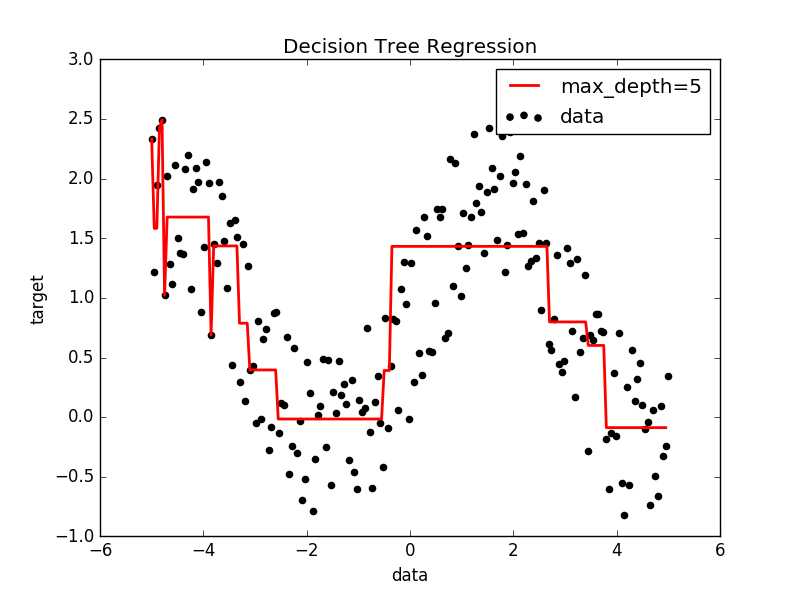
郑捷《机器学习算法原理与编程实践》学习笔记(第三章 决策树的发展)(三)_Scikit-learn与回归树
标签:current model sid res 数据集 决策 plot 准则 otl
原文地址:http://www.cnblogs.com/wuchuanying/p/6245477.html