标签:个数 tar ons targe 没有 接受 cache 数列 缓存
菲波那契数列,大致可以描叙为a(n) = a(n-1) + a(n-2) (a >=2)。类似于这样[1, 1, 2, 3, 5, 8, 13 ...]。
具体大家可以百度一下。下面我们来用js获取菲波那契数列的第N个数为多少:
1.递归
var a = function(n) { if (n === 1 || n === 2) { return 1 } else { return a(n - 1) + a(n - 2) } } console.time(‘a(44)‘) console.log(a(44)) console.timeEnd(‘a(44)‘)
以上我们可以比较清晰的看出代码的思路,但是这种方法有一个致命的缺点:效率太差!
不信你看:

执行到第44个的时候,已经不能接受了。需要5s多。那我们再来改进一下
--------------------------------------------------------------------------------
2.闭包+缓存
var b = (function() { var cache = { 1: 1, 2: 1 } return function(n) { if (cache[n]) { return cache[n] } else { cache[n - 1] = b(n - 1) cache[n - 2] = b(n - 2) return cache[n - 1] + cache[n - 2] } } })() console.time(‘b(1200)‘) console.log(b(1200)) console.timeEnd(‘b(1200)‘)
将每一步计算出来的值,保存到了缓存中。效率提升了许多:

------------------------------------------------------------------
3.直接计算出该数列的值得数组,然后再从数组中取值
var c = function(n) { var arr = [1, 1] if (n === 1 || n === 2) { return 1 } for (var i = 2; i < n; i ++) { arr[i] = arr[i - 1] + arr[i - 2] } return arr[n - 1] } console.time(‘c(1200)‘) console.log(c(1200)) console.timeEnd(‘c(1200)‘)
这样效率又进一步提高了不少:

那这样还有没有更快的方法呢?当然有!菲波那契数列是有数学表达式的:
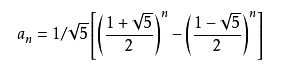
我们为何不直接使用数学表达式呢?
-----------------------------------------------------
4.直接使用数学表达式
var d = function(n) { return (1/(Math.pow(5, 1/2))) * (Math.pow((1 + Math.pow(5, 1/2))/2, n) - Math.pow((1 - Math.pow(5, 1/2))/2, n)) } console.time(‘d(1200)‘) console.log(d(1200)) console.timeEnd(‘d(1200)‘)
现在我们看一下效果:
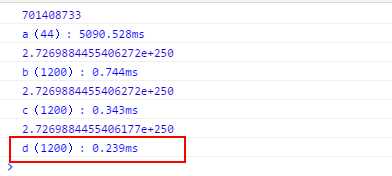
所以总结一下:数学真美!^_^
标签:个数 tar ons targe 没有 接受 cache 数列 缓存
原文地址:http://www.cnblogs.com/youweik/p/6285430.html