标签:setw 条件 fopen 不同 遍历 设计 函数 sort函数 oid
假设连通网N=(V,{E}),则令最小生成树的初始状态为只有n个顶点而无边的非连通图T=(V,{∮}),图中每个顶点自成一个连通分量。在E中选择代价最小的边,若该边依附的顶点落在T中不同的连通分量上,则将此边加入到T中,否则舍去此边而选择下一条代价最小的边。依次类推,直至T中所有顶点都在同一连通分量上为止。
(1)根据原图,构造一个只含n个顶点,边集为空的子图。若将图中各个顶点看成一棵树的根节点,则它是一个含有n棵树的森林。
(2)从网的边集 E 中选取一条权值最小的边,若该条边的两个顶点分属不同的树,则将其加入子图。也就是说,将这两个顶点分别所在的两棵树合成一棵树;反之,若该条边的两个顶点已落在同一棵树上,则不可取,而应该取下一条权值最小的边再试之
(3)依次类推,直至森林中只有一棵树,也即子图中含有 n-1条边为止。
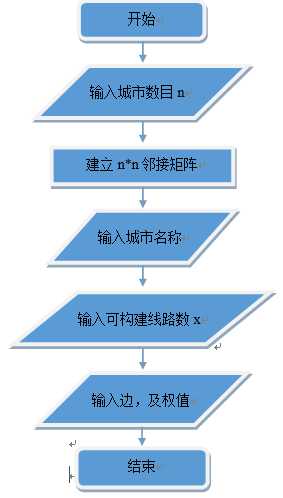
手动输入建立邻接矩阵:
首先输入城市数目n,建立n*n大小空矩阵。其次输入城市名称,并利用map函数使名称与数字可以相互转化。最后输入可构建线路的条数x,并输入x条边及权值填充邻接矩阵。
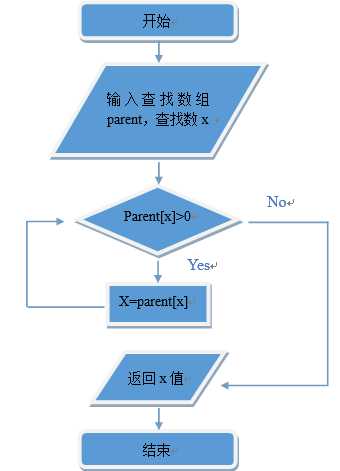
寻找根结点
根节点数组中保存对应的上一节点的值。依次往上寻找,知道数组中存储值为0,此时的参数即位目前的根节点。
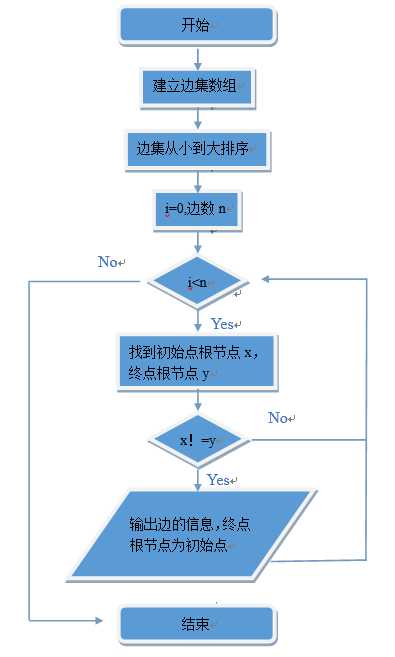
克鲁斯卡尔算法输出
建立边集数组,保证起始点的数值小于终点。利用sort函数,按权值将边从小到大排列。从小到大遍历所有边,查找每条边的起始点的根节点和终点的根节点。如果不同,证明加上这条边不会产生回路,输出这条边的信息,并使节点数组中终点的上一节点为初始点。
界面:


代码如下:

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <stdlib.h> 5 #include <algorithm> 6 #include <map> 7 #include <iomanip> 8 #include <fstream> 9 using namespace std; 10 11 #define max_city 100 //最大城市数 12 13 map <string,int> city_numbers; //城市->编号 14 15 map <int,string> numbers_city; //编号->城市 16 17 const int inf=0x3f3f3f3f; 18 19 typedef struct 20 { 21 int maps[max_city][max_city]; //邻接矩阵 22 int city_number; 23 int city_way; //城市数,线路数 24 } Graph ; 25 26 typedef struct 27 { 28 int way_begin; 29 int way_end; 30 int way_weight; 31 } Ways; 32 //线路集 33 34 void BuildGraph1(Graph *this_graph) 35 { 36 printf("请输入城市数(按回车键结束输入):\n"); 37 cin>>this_graph->city_number; 38 39 for (int i=0;i<this_graph->city_number;i++) 40 { 41 for(int j=0;j<this_graph->city_number;j++) 42 { 43 if (i==j) 44 this_graph->maps[i][j]=0; 45 else 46 this_graph->maps[i][j]=this_graph->maps[j][i]=inf; 47 } 48 } 49 50 printf("请输入城市名称(城市名字之间用空格隔开,按回车键结束输入):\n"); 51 for(int i=0;i<this_graph->city_number;i++) 52 { 53 char name[1000]; 54 cin>>name; 55 city_numbers[name]=i; 56 numbers_city[i]=name; 57 } 58 59 printf("请输入可构架线路数(按回车键结束输入):\n"); 60 cin>>this_graph->city_way; 61 62 printf("请输入每条线路两端的城市名及权值:\n"); 63 for(int i=0;i<this_graph->city_way;i++) 64 { 65 char start[1000],last[1000]; 66 int weight; 67 printf("请输入第%d条线路(城市名及权值用空格隔开,每条线路按回程键结束输入):\n",i+1); 68 69 cin>>start>>last>>weight; 70 this_graph->maps[city_numbers[start]][city_numbers[last]]=this_graph->maps[city_numbers[last]][city_numbers[start]]=weight; 71 } 72 73 } 74 //手动输入信息 75 76 bool BuildGraph2(Graph *this_graph) 77 { 78 FILE *fp; 79 char address[1000]; 80 printf("请输入文件的地址(按回车键结束输入):\n"); 81 cin>>address; 82 83 if((fp=fopen(address,"r"))==NULL) 84 return false; 85 86 if(fscanf(fp,"%d",&this_graph->city_number)==EOF) 87 return false; 88 89 for (int i=0;i<this_graph->city_number;i++) 90 { 91 for(int j=0;j<this_graph->city_number;j++) 92 { 93 if (i==j) 94 this_graph->maps[i][j]=0; 95 else 96 this_graph->maps[i][j]=this_graph->maps[j][i]=inf; 97 } 98 } 99 100 for(int i=0;i<this_graph->city_number;i++) 101 { 102 char name[1000]; 103 if(fscanf(fp,"%s",name)==EOF) 104 return false ; 105 city_numbers[name]=i; 106 numbers_city[i]=name; 107 } 108 109 if(fscanf(fp,"%d",&this_graph->city_way)==EOF) 110 return false; 111 112 for(int i=0;i<this_graph->city_way;i++) 113 { 114 char start[1000],last[1000]; 115 int weight; 116 if(fscanf(fp,"%s%s%d",start,last,&weight)==EOF) 117 return false; 118 this_graph->maps[city_numbers[start]][city_numbers[last]]=this_graph->maps[city_numbers[last]][city_numbers[start]]=weight; 119 } 120 121 fclose(fp); 122 return true; 123 } 124 //从文件读入信息 125 126 bool cmp(Ways first,Ways last) 127 { 128 return first.way_weight<last.way_weight; 129 } 130 //排序条件 131 132 int find_parent(int parent[],int find_city) 133 { 134 while(parent[find_city]>0) 135 { 136 find_city=parent[find_city]; 137 } 138 return find_city; 139 } 140 //寻找根节点 141 142 void Putout1(Graph this_graph) 143 { 144 int num=0; 145 int parent[max_city]; 146 Ways way[max_city]; 147 memset(parent,0,sizeof(parent)); 148 149 for (int i=0;i<this_graph.city_number;i++) 150 { 151 for(int j=i+1;j<this_graph.city_number;j++) 152 { 153 if(this_graph.maps[i][j]!=inf) 154 { 155 way[num].way_begin=i; 156 way[num].way_end=j; 157 way[num++].way_weight=this_graph.maps[i][j]; 158 } 159 } 160 } 161 //建立边集 162 163 sort(way,way+num,cmp); 164 //边集排序 165 166 int sum=0; 167 printf("最低经济方案如下如下:\n"); 168 cout<<"编号"<<setw(8)<<"城市1"<<setw(8)<<"城市2"<<setw(8)<<"权值"<<endl; 169 for (int i=0;i<this_graph.city_way;i++) 170 { 171 int n=find_parent(parent,way[i].way_begin); 172 int m=find_parent(parent,way[i].way_end); 173 //寻找首位两点的根 174 175 if (n != m) 176 { 177 parent[n] = m; 178 char city1[1000],city2[1000]; 179 cout<<++sum<<setw(8)<<numbers_city[way[i].way_begin]<<setw(8)<<numbers_city[way[i].way_end]<<setw(8)<<way[i].way_weight<<endl; 180 } 181 //假如n与m不等,说明两个顶点不会产生回路 182 } 183 } 184 //直接输出结果 185 186 bool Putout2(Graph this_graph) 187 { 188 int num=0; 189 int parent[max_city]; 190 Ways way[max_city]; 191 memset(parent,0,sizeof(parent)); 192 193 for (int i=0;i<this_graph.city_number;i++) 194 { 195 for(int j=i+1;j<this_graph.city_number;j++) 196 { 197 if(this_graph.maps[i][j]!=inf) 198 { 199 way[num].way_begin=i; 200 way[num].way_end=j; 201 way[num++].way_weight=this_graph.maps[i][j]; 202 } 203 } 204 } 205 //建立边集 206 207 sort(way,way+num,cmp); 208 //边集排序 209 210 fstream fp; 211 printf("请输入文件的地址(按回车键结束输入):\n"); 212 int sum=0; 213 char address[1000]; 214 cin>>address; 215 fp.open(address); 216 217 if(!fp) 218 return false; 219 fp<<"最低经济方案如下如下:"<<endl; 220 fp<<"编号"<<setw(8)<<"城市1"<<setw(8)<<"城市2"<<setw(8)<<"权值"<<endl; 221 for (int i=0;i<this_graph.city_way;i++) 222 { 223 int n=find_parent(parent,way[i].way_begin); 224 int m=find_parent(parent,way[i].way_end); 225 //寻找首位两点的根 226 227 if (n != m) 228 { 229 parent[n] = m; 230 char city1[1000],city2[1000]; 231 fp<<++sum<<setw(8)<<numbers_city[way[i].way_begin]<<setw(8)<<numbers_city[way[i].way_end]<<setw(8)<<way[i].way_weight<<endl; 232 } 233 } 234 //假如n与m不等,说明两个顶点不会产生回路 235 return true; 236 } 237 //打印到文件中 238 239 int main() 240 { 241 int ch; 242 243 while(true) 244 { 245 246 printf("|-------------------------------------------------------|\n"); 247 printf("|\t\t\t\t\t\t\t|\n"); 248 printf("|\t\t 欢迎进入最小生成树系统! \t\t|\n"); 249 printf("|\t\t\t\t\t\t\t|\n"); 250 printf("|-------------------------------------------------------|\n"); 251 printf("|\t\t\t\t\t\t\t|\n"); 252 printf("|\t\t 1——手动输入信息 \t\t|\n"); 253 printf("|\t\t 2——从文件读入信息 \t\t|\n"); 254 printf("|\t\t 0——退出系统 \t\t|\n"); 255 printf("|\t\t\t\t\t\t\t|\n"); 256 printf("|-------------------------------------------------------|\n"); 257 printf("请输入选项编号(0 ~ 2): (按回车键结束输入)\n"); 258 259 Graph this_graph; 260 cin>>ch; 261 262 if(ch==0) 263 break; 264 265 if(ch==1) 266 BuildGraph1(&this_graph); 267 268 else if(ch==2) 269 { 270 if(!BuildGraph2(&this_graph)) 271 { 272 printf("打开文件读入信息失败!\n"); 273 continue; 274 } 275 printf("打开文件读入信息成功!\n"); 276 } 277 278 printf("|-------------------------------------------------------|\n"); 279 printf("|\t\t\t\t\t\t\t|\n"); 280 printf("|\t\t 1——直接输出结果 \t\t|\n"); 281 printf("|\t\t 2——输出到文件 \t\t|\n"); 282 printf("|\t\t 0——退出系统 \t\t|\n"); 283 printf("|\t\t\t\t\t\t\t|\n"); 284 printf("|-------------------------------------------------------|\n"); 285 printf("请输入选项编号(0 ~ 2): (按回车键结束输入)\n"); 286 287 cin>>ch; 288 if(ch==0) 289 break; 290 291 if(ch==1) 292 Putout1(this_graph); 293 294 else if(ch==2) 295 { 296 if(!Putout2(this_graph)) 297 { 298 printf("打开文件输入信息失败!\n"); 299 continue; 300 } 301 printf("打开文件输入信息成功!\n"); 302 } 303 } 304 }
标签:setw 条件 fopen 不同 遍历 设计 函数 sort函数 oid
原文地址:http://www.cnblogs.com/kingbk/p/6286898.html