R语言实战（五）方差分析与功效分析

标签：比较   center   plot   抽样   阵列   求和   默认   范围   nbsp   

 ====================================================================

方差分析：

回归分析是通过量化的预测变量来预测量化的响应变量，而解释变量里含有名义型或有序型因子变量时，我们关注的重点通常会从预测转向组别差异的分析，这种分析方法就是方差分析（ANOVA）。因变量不只一个时，称为多元方差分析（MANOVA）。有协变量时，称为协方差分析（ANCOVA）或多元协方差分析（MANCOVA）。

#基本格式
aov(formula, data = dataframe)

基本表达式符号参考回归中的表格

研究设计的表达式

下表中，小写字母表示定量变量，大写字母表示组别因子，Subject是对被试者独有的标识变量

表达式中的各项顺序：

有两种情况会造成影响：（1）因子不止一个，并且是非平衡设计；（2）存在协变量。出现任意一种情况时，等式右边的变量都与其他每个变量相关，此时我们无法清晰地划分它们对因变量的影响。

例如，对于双因素方差分析，若不同处理方式中的观测数不同，那么模型y ~ A * B与模型y ~ B * A的结果不同

R默认类型1（序贯型）方法计算ANOVA效应。第一个模型可以这样写：y ~ A + B + A : B

R中的ANOVA表的结果将评价：

1. A对y的影响
2. 控制A时，B对y的影响
3. 控制A和B的主效应时，A与B的交互效应

样本大小越不平衡，效应项的顺序对结果的影响越大。一般来说，越基础性的效应越需要放在表达式前面。

具体来讲，首先是协变量，然后是主效应，接着是双因素的交互项，再接着是三因素的交互项，以此类推。

对于主效应，越基础性的变量越应放在表达式前面，比如性别要放在处理方式之前。有一个基本准则：若研究设计不是正交的（即因子与协变量相关），一定要谨慎设置效应的顺序。

需要注意的是，car包中的Anova()函数提供了类型2和类型3方法的选项，而aov()函数使用的是类型1方法。若想使结果与其他软件提供的结果保持一致，可以使用Anova()函数。

单因素方差分析：

多重比较：

#各组均值差异的成对检验
TukeyHSD(fit)

#glht()函数提供了更为全面的方法，适用于线性模型和广义线性模型
library(multcomp)
tuk <- glht(fit, linfct = mcp(trt = “Tukey”))
plot(cld(tuk, level = 0.05), col = “lightgrey”)

评估检验的假设条件： 

单因素方差分析的假设条件：因变量服从正态分布；各组方差相等。

#Q-Q图检验正态性假设
library(car)
qqPlot(lm(response ~ trt, data = cholesterol), simulate = TRUE, labels = FALSE)
#数据落在95%置信区间范围内，说明满足正态性假设

#方差齐性检验（Bartlett检验）
bartlett.test(response ~ trt, data = cholesterol)
#p大于0.05说明没有显著不同
 
#方差齐性分析对离群点非常敏感，需要补做一次离群点的检测
library(car)
outlierTest(fit)
#若没有离群点，说明上述结果较为可信

单因素协方差分析： 

#单因素ANCOVA
data(litter, package = “multcomp”)
attach(litter)
table(dose)
aggregate(weight, by = list(dose), FUN = mean)
fit <- aov(weight ~ gesttime + dose)
summary(fit)
 
#获取调整的组均值（即去除协变量效应后的组均值）
library(effects)
effect(“dose”, fit)

评估检验的假设条件： 

单因素协方差分析的假设条件：正态性、同方差性。

与单因素方差分析的假设条件判断相同。

结果可视化：

library(HH)
ancova(weight ~ gesttime + dose, data = litter)

双因素方差分析：

#table()函数观察是否是均衡设计
attach(ToothGrowth)
table(supp, dose)
aggregate(len, by = list(supp, dose), FUN = mean)
aggregate(len, by = list(supp, dose), FUN = sd)
fit <- aov(len ~ supp*dose)
summary(fit)
 
#可视化处理
interaction.plot(dose, supp, len, type = “b”,
col = c(“red”, “blue”), pch = c(16, 18),
main = “Interaction between Dose and Supplement Type”)
#或者是
library(gplots)
plotmeans(len ~ interaction(supp, dose, sep = “ ”),
connect = list(c(1, 3, 5), c(2, 4, 6)),
col = c(“red”, “darkgreen”),
main = “Interaction Plot with 95% CIs”,
xlab = “Treatment and Dose Combination”)
#也可以（推荐）
library(HH)
interaction2wt(len ~ supp * dose)

重复测量方差分析：受试者被测量不止一次，重点关注含一个组内和一个组间因子的重复测量方差分析。 

混合模型设计概述：

由于传统的重复测量方差分析假设任意组内因子的协方差矩阵为球形，并且任意组内因子两水平间的方差之差都相等。但在现实中这种假设不可能满足，于是衍生了一系列备选方法：

使用lme4包中的lmer()函数拟合线性混合模型；

使用car包中的Anova()函数调整传统检验统计量以弥补球形假设的不满足（例如Geisser-Greenhouse校正）；

使用nlme包中的gls()函数拟合给定方差-协方差结构的广义最小二乘模型；

用多元方差分析对重复测量数据进行建模。

多元方差分析：

当因变量（结果变量）不止一个时，可用多元方差分析（MANOVA）对它们同时进行分析。

评估假设检验：单因素多元方差分析的假设前提，一个是多元正态性，一个是方差-协方差矩阵同质性。

多元正态性假设即指因变量组合成的向量服从一个多元正态分布，可以用Q-Q图来检验该假设条件。方差-协方差矩阵同质性即指各组的协方差矩阵相同，通常可用Box’s M检验来评估该假设。

最后可使用mvoutlier包中的aq.plot()函数来检验多元离群点。

library(mvoutlier)
outliers <- aq.plot(y)
ouliers

稳健多元方差分析： 

如果多元正态性或者方差-协方差均值假设都不满足，又或者担心多元离群点，那么可以考虑用稳健或非参数版本的MANOVA检验。

稳健单因素MANOVA可通过rrcov包中的Wilks.test()函数实现。vegan包中的adonis()函数则提供了非参数MANOVA的等同形式。

#Wilks.test()函数应用示例
library(rrcov)
Wilks.test(y, shelf, method = “mcd”)

用回归做ANOVA： 

事实上，ANOVA和回归都是广义线性模型的特例。因此可以用lm()函数来分析。

这部分看不大懂，以后再回头看吧。

=========================================================================

功效分析：

功效分析可以帮助在给定置信度的情况下，判断检测到给定效应值时所需的样本量。反过来，它也可以帮助你在给定置信度水平情况下，计算在某样本量内能检测到给定效应值的概率。如果概率低得难以接受，修改或者放弃这个实验将是一个明智的选择。

本章中将学习如何对多种统计检验进行功效分析，包括比例检验、t检验、卡方检验、平衡的单因素ANOVA、相关性分析，以及线性模型分析。由于功效分析针对的是假设检验，我们将首先简单回顾零假设显著性检验（NHST）过程，然后学习如何用R进行功效分析，主要关注于pwr包。

假设检验回顾：

首先对总体分布参数作零假设H0, 从总体分布中抽样，通过样本计算统计量对总体参数进行推断。假定H0为真，如果计算获得的观测样本的统计量的概率非常小，便可以拒绝原假设，接受备择假设H1。

Ⅰ型错误：H0为真却拒绝H0

Ⅱ型错误：H0为假却不拒绝H0

研究过程中，研究者通常关注四个量：

样本大小：实验设计中每种条件/组中观测的数目

显著性水平（即alpha，也就是概率p的阈值）：Ⅰ型错误的概率

功效：（1-P(Ⅱ型错误)）可以看作是真是效应发生的概率

效应值：指的是在备择或研究假设下效应的量。效应值的表达式依赖于假设检验中使用的统计方法

这四个量紧密相关，给定其中任意三个量，便可推算第四个量。本章就是利用这一点进行各种各样的功效分析。

pwr包中的函数

t检验

pwr.t.test(n = , d = , sig.level = , power = , alternative = )

n为样本大小 

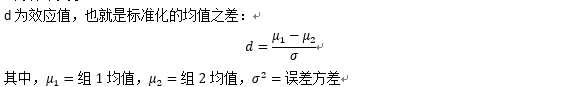
sig.level表示显著性水平，默认0.05

power为功效水平

type指检验类型：双样本t检验（two.sample）、单样本检验（one.sample）或相依样本t检验（paired）默认为双样本t检验。

alternative指统计检验是双侧检验（two.sided）还是单侧检验（less或greater）。默认双侧

方差分析

pwr.anova.test(k = , n = , f = , sig.level = , power = )

相关性

pwr.r.test(n = , r = , sig.level = , power = , alternative = )

其中，n是观测数目，r是效应值（通过线性相关系数衡量），sig.level是显著性水平，power是功效水平，alternative指定显著性检验是双边检验（two.sided）还是单边检验（less或greater） 

线性模型

pwr.f2.test(u = , v = , f2 = , sig.level = , power = )

当要评价一组预测变量对结果的影响程度时，适宜用第一个公式计算f2；当要评价一组预测变量对结果的影响超过第二组变量（协变量）多少时，适宜用第二个公式。

比例检验

pwr.2p.test(h = , n = , sig.level = , power = )

其中，h是效应值，n是各组相同的样本量。效应值h定义如下： 

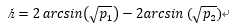
可用ES.h(p1, p2)函数进行计算

当各组n不相同时：

pwr.2p2n.test(h = , n1 = , n2 = , sig.level = , power = )

同样，alternative可以设定单边检验或双边检验（默认）

卡方检验

卡方检验常常用来评价两个类别型变量的关系：典型的零假设是变量之间独立，备择假设是不独立。

pwr.chisq.test(w = , N = , df = , sig.level = , power = )

其中，w是效应值，N是总样本大小，df是自由度。 

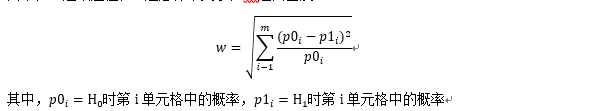
此处从1到m进行求和，连加号上的m指的是列联表中单元格的数目。函数ES.w2(P)可以计算双因素列联表中备择假设的效应值，P是一个假设的双因素概率表。

新情况中选择合适的效应值：

功效分析中，预期效应值是最难决定的参数。通常需要你对主题有一定的了解，并有相应的测量经验。当没有经验时，可以用一个基准进行参考，该基准由Cohen(1988)提出，可为各种统计检验划分小、中、大三种效应值：

但是要注意，这个参考仅仅是参考，是一般性建议，特殊的研究领域内可能不适用。

绘制功效分析图形：使用for循环将样本量与相关系数之间的关系可视化出来，用图来判断需要的样本量。

其他专业化的功效分析软件包：

R语言实战（五）方差分析与功效分析

标签：比较   center   plot   抽样   阵列   求和   默认   范围   nbsp   

原文地址：http://www.cnblogs.com/gyjerry/p/6287811.html