标签:归并 logs stream 整合 code list int font 非递归
1.非递归方法
分成三个函数,用来实现三个功能:
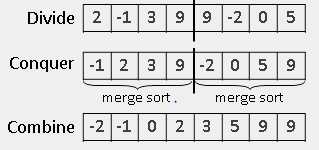
总体实现过程:
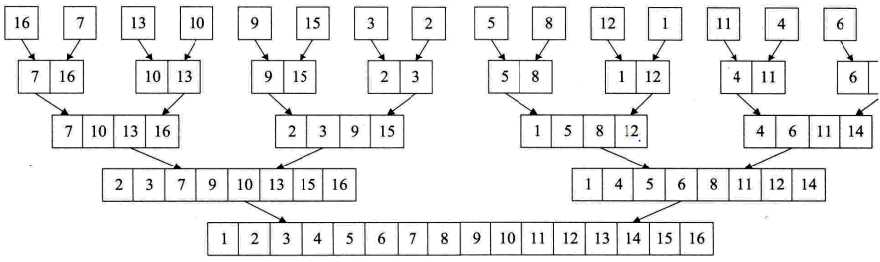
第一个函数:Merge,用来实现合并两段有序的序列 :[2,5,7,9,3,8,10]->[2,3,5,7,8,9,10] 。i=0,m=3,n=6.
#include<iostream> #include<algorithm> using namespace std; void Merge(int SR[],int TR[],int i,int m,int n){ //将SR中首元素位置i,第一段有序序列末位m,SR中末位为n的两段序列合并 int j = m + 1 , k=i; while ((i <= m) && (j <= n)) { if (SR[i] < SR[j]){ TR[k++] = SR[i]; i = i + 1; } if (SR[i] > SR[j]){ TR[k++] = SR[j]; j = j + 1; } } while (i <= m) TR[k++] = SR[i++]; while (j <= n) TR[k++] = SR[j++]; } int main(){ //测试 int sr[] = { 10, 20, 30, 45, 50, 62, 63, 5, 15, 40, 55, 60, 99 }; int n = (sizeof(sr) / sizeof(sr[0])); int tr[13] = {}; Merge(sr, tr, 0, 6, 12); for (int i = 0; i < n; i++) cout << tr[i] << ‘ ‘; cout << endl; }
测试结果:
第二个函数:MergePass,用来实现每两个长度为s的串合并。注意这个函数分成以下三种情况但(仅以s=3为例):
#include<iostream> #include<algorithm> using namespace std; void MergePass(int SR[], int TR[],int s,int n){ //将SR中每两个长度为s的串合并到TR中 int i=0, j ; for (j = 0; j <= n / (2 * s) - 1; j++) //完整合并次数 { if (2 * s + i - 1 <= n) { Merge(SR, TR, i, i + s - 1, i + 2 * s - 1); i = i + 2 * s; } } if (s + i-1 <n) //剩余元素数目大于s { Merge(SR, TR, i, i + s - 1, n - 1); } else //剩余元素数目小于等于s { j = i; while (j <= n - 1) TR[j++] = SR[i++]; } } int main(){ //测试 int ssr[] = {1,2,4,3,5,6,13,28,37,0,11,19,26,79}; int ttr[14] = {}; int ssr_n = 14; MergePass(ssr, ttr, 3, ssr_n); //每两个长度为3的串合并 for (int i = 0; i < ssr_n; i++) cout << ttr[i] << ‘ ‘; cout << endl; }
测试结果:
第三个函数:放在main里面了,通过SR和TR数组来回合并实现归并排序。以下是归并排序代码:MergeSort.cpp
#include<iostream> #include<algorithm> using namespace std; void Merge(int SR[],int TR[],int i,int m,int n){ int j = m + 1 , k=i; while ((i <= m) && (j <= n)) { if (SR[i] < SR[j]){ TR[k++] = SR[i]; i = i + 1; } if (SR[i] > SR[j]){ TR[k++] = SR[j]; j = j + 1; } } while (i <= m) TR[k++] = SR[i++]; while (j <= n) TR[k++] = SR[j++]; } void MergePass(int SR[], int TR[],int s,int n){ int i=0, j ; for (j = 0; j <= n / (2 * s) - 1; j++) { if (2 * s + i - 1 <= n) { Merge(SR, TR, i, i + s - 1, i + 2 * s - 1); i = i + 2 * s; } } if (s + i-1 <n) { Merge(SR, TR, i, i + s - 1, n - 1); } else { j = i; while (j <= n - 1) TR[j++] = SR[i++]; } } int main(){ //测试 int test_sr[] = { 11, 4, 7, 2, 6, 109, 3, 87, 53, 8, 22, 66, 36, 23, 51, 33, 57, 62, 77, 0, 1 }; int test_sr_n = (sizeof(test_sr) / sizeof(test_sr[0])); int *test_tr = (int *)malloc(test_sr_n*sizeof(int)); int k = 1; //k=1,意味着每两个长度为1的串合并,后来k以2倍增长! while (k < test_sr_n) { MergePass(test_sr, test_tr, k, test_sr_n); //将test_sr中的元素按照每两个长度为k的串归并至test_tr中 k = 2 * k; for (int i = 0; i < test_sr_n; i++) //打印test_tr中的元素,观察归并过程 cout << test_tr[i] << ‘ ‘; cout << endl; MergePass(test_tr, test_sr, k, test_sr_n); //将test_tr中的元素按照每两个长度为k的串归并至test_sr中 k = 2 * k; for (int i = 0; i < test_sr_n; i++) //打印test_sr中的元素,观察归并过程 cout << test_sr[i] << ‘ ‘; cout << endl; } }
测试结果:
2.递归方法
示意图:
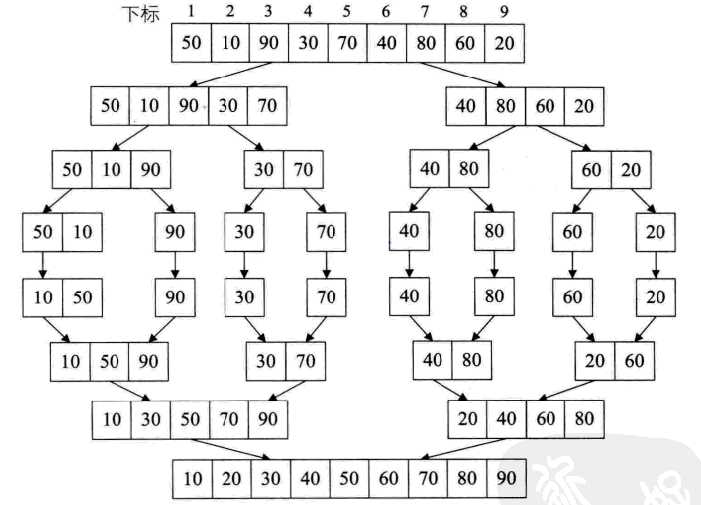
#include<iostream> #include<algorithm> using namespace std; void Merge(int SR[],int TR[],int i,int m,int n){ int j = m + 1 , k=i; while ((i <= m) && (j <= n)) { if (SR[i] < SR[j]){ TR[k++] = SR[i]; i = i + 1; } if (SR[i] > SR[j]){ TR[k++] = SR[j]; j = j + 1; } } while (i <= m) TR[k++] = SR[i++]; while (j <= n) TR[k++] = SR[j++]; } void MSort(int SR[], int TR1[], int s, int t){ //将SR[s..t]归并为TR1[s..t] int m; int TR2[21]; if (s == t) TR1[s] = SR[s]; else { m = (s + t) / 2; //将SR[s..t}平分为[s..m]和[m+1..t] MSort(SR, TR2, s, m); //归并前半部分为有序序列 MSort(SR, TR2, m + 1, t); //归并后半部分为有序序列 Merge(TR2, TR1, s, m, t); //将TR2中两部分[s,m]和[m+1,t]序列归并到TR1中 } }
int main(){ int test_sr[] = { 11, 4, 7, 2, 6, 109, 3, 87, 53, 8, 22, 66, 36, 23, 51, 33, 57, 62, 77, 0, 1 }; int test_sr_n = (sizeof(test_sr) / sizeof(test_sr[0])); int *test_tr = (int *)malloc(test_sr_n*sizeof(int)); MSort(test_sr, test_tr, 0, test_sr_n-1); for (int i = 0; i < test_sr_n; i++) cout << test_tr[i] << ‘ ‘; cout << endl; }
程序结果:
标签:归并 logs stream 整合 code list int font 非递归
原文地址:http://www.cnblogs.com/king-lps/p/6349632.html