标签:blank trap 路径问题 sina nbsp images space cto int
一,贪心算法的设计思想
? 从问题的某一个初始解出发逐步逼近给定的目标,每一步都作一个不可回溯的决策,尽可能地求得最好的解。当达到某算法中的某一步不需要再继续前进时,算法停止。
二,贪心算法的基本性质
1)贪心选择性质
所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。这是贪心算法可行的第一个基本要素,也是贪心法与动态规划法的主要区别。
2) 最优子结构性质
该问题解的整体最优性依赖于其局部子问题解的最优性。这种性质是可以采用贪心算法解决问题的关键特征。例如,活动安排问题,在选择了一项活动后,它必须是最优的,否则不能得到全局的最优。
三,贪心算法的适用性
? 贪心算法对问题只需考虑当前局部信息就要做出决策,也就是说使用贪心算法的前提是“局部最优策略能导致产生全局最优解”。
?该算法的适用范围较小, 若应用不当, 不能保证求得问题的最佳解。更准确的方法是通过数学方法证明问题对贪心策略的选用性。
例一、单源最短路径问题(有向图)
单源最短路径问题,即在图中求出给定顶点到其它任一顶点的最短路径。在弄清楚如何求算单源最短路径问题之前,必须弄清楚最短路径的最优子结构性质。
一.最短路径的最优子结构性质
该性质描述为:如果P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径,k和s是这条路径上的一个中间顶点,那么P(k,s)必定是从k到s的最短路径。下面证明该性质的正确性。
假设P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径,则有P(i,j)=P(i,k)+P(k,s)+P(s,j)。而P(k,s)不是从k到s的最短距离,那么必定存在另一条从k到s的最短路径P‘(k,s),那么P‘(i,j)=P(i,k)+P‘(k,s)+P(s,j)<P(i,j)。则与P(i,j)是从i到j的最短路径相矛盾。因此该性质得证。
二.Dijkstra算法
由上述性质可知,如果存在一条从i到j的最短路径(Vi.....Vk,Vj),Vk是Vj前面的一顶点。那么(Vi...Vk)也必定是从i到k的最短路径。为了求出最短路径,Dijkstra就提出了以最短路径长度递增,逐次生成最短路径的算法。譬如对于源顶点V0,首先选择其直接相邻的顶点中长度最短的顶点Vi,那么当前已知可得从V0到达Vj顶点的最短距离dist[j]=min{dist[j],dist[i]+matrix[i][j]}。根据这种思路,
假设存在G=<V,E>,源顶点为V0,U={V0},dist[i]记录V0到i的最短距离,path[i]记录从V0到i路径上的i前面的一个顶点。
1.从V-U中选择使dist[i]值最小的顶点i,将i加入到U中;
2.更新与i直接相邻顶点的dist值。(dist[j]=min{dist[j],dist[i]+matrix[i][j]})
3.知道U=V,停止。
算法流程:
(a) 初始化:用起点v到该顶点w的直接边(弧)初始化最短路径,否则设为∞;
(b)
从未求得最短路径的终点中选择路径长度最小的终点u:即求得v到u的最短路径;
(c)
修改最短路径:计算起点v到u的邻接点的最短路径,若(v,…,u)+(u,w)<(v,…,w),则以(v,…,u,w)代替。
(d)
重复(b)-(c),直到求得v到其余所有顶点的最短路径。
特点:总是按照从小到大的顺序求得最短路径。
/*Dijkstra求单源最短路径 */ #include <iostream> #include<stack> #include<vector> #include"stdlib.h" #define M 100 #define N 100 using namespace std; typedef struct node { int matrix[N][M]; //邻接矩阵 int n; //顶点数 int e; //边数 }MGraph; void DijkstraPath(MGraph g,vector<int> &dist,vector<int> &path,int v0) //v0表示源顶点 { int i,j,k; vector<bool> visited=vector<bool>(g.n); for(i=0;i<g.n;i++) //初始化,用起点v到直接相邻顶点i的边(弧)初始化最短路径,否则设为∞; { if(g.matrix[v0][i]>0&&i!=v0) { dist[i]=g.matrix[v0][i]; path[i]=v0; //path记录最短路径上从v0到i的前一个顶点 } else { dist[i]=INT_MAX; //若i不与v0直接相邻,则权值置为无穷大 path[i]=-1; } visited[i]=false; //初始化所有顶点为未扩展 path[v0]=v0; dist[v0]=0; } visited[v0]=true; for(i=1;i<g.n;i++) //循环扩展n-1次 { int min=INT_MAX; int u; for(j=0;j<g.n;j++) //寻找未被扩展的权值最小的顶点 { if(visited[j]==false&&dist[j]<min) { min=dist[j]; u=j; } } visited[u]=true; for(k=0;k<g.n;k++) //更新dist数组的值和路径的值,计算起点v到u的邻接点的最短路径,若(v,…,u)+(u,w)<(v,…,w),则以(v,…,u,w)代替 { if(visited[k]==false&&g.matrix[u][k]>0&&min+g.matrix[u][k]<dist[k]) { dist[k]=min+g.matrix[u][k]; path[k]=u; } } } } void showPath(vector<int> & path,int v,int v0) //输出起点v0到顶点i的最短路径上的各个顶点 { stack<int> s; int u=v; while(v!=v0) //逆向遍历,将最低按路径入栈 { s.push(v); v=path[v]; } s.push(v); cout<< "起点" <<v0<<"到顶点" <<v<<"的最短路径:" ; while(!s.empty()) { cout<<s.top()<<" "; s.pop(); } } int main(int argc, char *argv[]) { int n,e; //表示输入的顶点数和边数 while(cin>>n>>e&&e!=0) { int i,j; int s,t,w; //表示存在一条边s->t,权值为w MGraph g; int v0; vector<int> dist=vector<int>(n); vector<int> path=vector<int>(n); for(i=0;i<N;i++) for(j=0;j<M;j++) g.matrix[i][j]=0; g.n=n; g.e=e; for(i=0;i<e;i++) { cin>>s>>t>>w; g.matrix[s][t]=w; } cin>>v0; //输入源顶点 DijkstraPath(g,dist,path,v0); for(i=0;i<n;i++) { if(i!=v0) { showPath(path,i,v0); cout<<dist[i]<<endl; } } } return 0; }
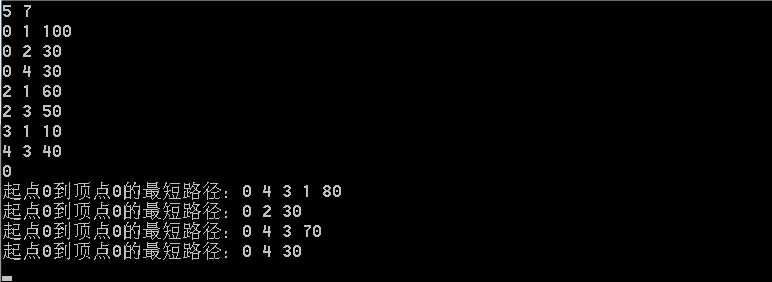
以上是求起点到任意一点的最短距离,若要求
利用贪心算法解题,需要解决两个问题:
一是问题是否适合用贪心法求解。我们看一个找币的例子,如果一个货币系统有三种币值,面值分别为一角、五分和一分,求最小找币数时,可以用贪心法求解;如果将这三种币值改为一角一分、五分和一分,就不能使用贪心法求解。用贪心法解题很方便,但它的适用范围很小,判断一个问题是否适合用贪心法求解,目前还没有一个通用的方法,在信息学竞赛中,需要凭个人的经验来判断。
二是确定了可以用贪心算法之后,如何选择一个贪心标准,才能保证得到问题的最优解。在选择贪心标准时,我们要对所选的贪心标准进行验证才能使用,不要被表面上看似正确的贪心标准所迷惑。
标签:blank trap 路径问题 sina nbsp images space cto int
原文地址:http://www.cnblogs.com/wujing-hubei/p/6375906.html