标签:没有 顶点 广度 ted 复杂度 遍历 入队 元素 .com
样图:
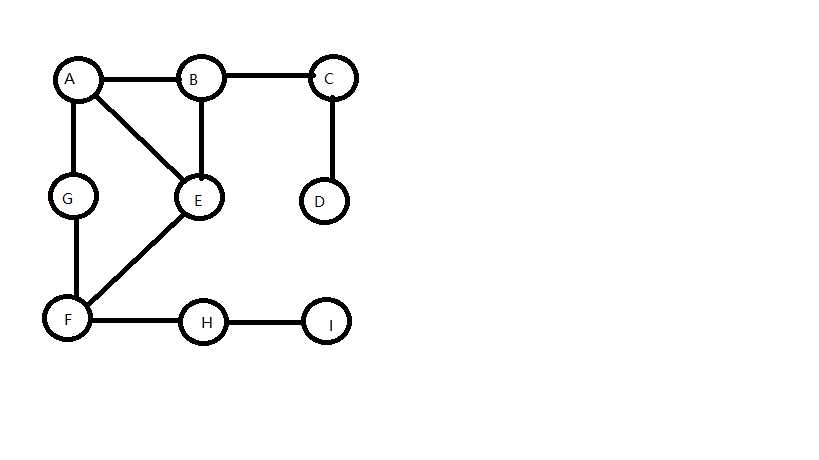
DFS:深度优先搜索,是一个不断探查和回溯的过程,每探查一步就将该步访问位置为true,接着在该点所有邻接节点中,找出尚未访问过的一个,将其作为下个探查的目标,接着对这个目标进行相同的操作,直到回到最初的节点,此时图中所有节点都访问过了。
BFS:广度优先搜索,是一个逐层遍历的过程,每探查一步就将该步访问位置为true,接着在该点所有邻接节点中,找出尚未访问过的一个,将其作为下个探查的目标,接着还是对该节点(而不是所选择的目标)剩下的未访问的点选择一个,作为下一个探查的目标,直到没有邻接点为止。这些探测过的点存放于一个队列中,当该节点没有邻接节点时,取出队首的点进行相同的操作,直到队列为空,此时图中所有节点都访问过了。
实现代码(邻接矩阵法和邻接表法):
邻接矩阵法:(时间复杂度n^2),n代表顶点
1 #include<iostream> 2 #include<queue> 3 #define maxValue 100 4 using namespace std; 5 template<class E> 6 class Graph{//图的邻接矩阵表示(无向图) 7 public: 8 Graph(int n){ 9 numV=n; 10 vlist=new int[n]; 11 visited=new bool[n]; 12 edge=new E*[n]; 13 for(int i=1;i<n;i++){ 14 vlist[i]=i; 15 edge[i]=new E[n]; 16 visited[i]=false; 17 } 18 visited[0]=true; 19 for(int i=0;i<n;i++){ 20 for(int j=0;j<n;j++){ 21 edge[i][j]=(i==j)?0:maxValue; 22 } 23 } 24 } 25 ~Graph(){ 26 delete []vlist; 27 delete []edge; 28 delete []visited; 29 } 30 int getFirst(int v){//获取顶点V的第一个邻接点 31 for(int col=0;col<numV;col++) 32 if(edge[v][col]>0&&edge[v][col]<maxValue) 33 return col; 34 return -1; 35 } 36 int getNext(int v,int w){//获取顶点V的某个邻接点w的下一个 邻接点 37 for(int col=w+1;col<numV;col++) 38 if(edge[v][col]>0&&edge[v][col]<maxValue) 39 return col; 40 return -1; 41 } 42 bool removeV(int v){//删除一个定点上的所有关联边 43 for(int i=0;i<numV;i++){ 44 if(i!=v){ 45 edge[v][i]=maxValue; 46 edge[i][v]=maxValue; 47 } 48 } 49 } 50 bool insertE(int v1,int v2,E cost){//插入边V1,V2 51 edge[v1][v2]=edge[v2][v1]=cost; 52 } 53 bool removeE(int v1,int v2){//删除边V1,V2 54 edge[v1][v2]=edge[v2][v1]=maxValue; 55 } 56 E getW(int v1,int v2){//返回边(v1,v2)上的权值 57 return edge[v1][v2]; 58 } 59 void DFS(int v){//深度优先搜索 60 cout<<(char)(vlist[v]+64)<<" ";//打印节点 61 visited[v]=true;//标记该节点被访问过 62 int w=getFirst(v);//w为节点v的第一个邻接节点 63 while(w!=-1){//v仍有临接节点未访问完 64 if(visited[w]==false) DFS(w);//如果w未被访问,对w进行新一轮DFS 65 w=getNext(v,w);//w重新设置成v的下一个临接节点 66 } 67 } 68 void BFS(int v){//广度优先搜索 69 cout<<(char)(vlist[v]+64)<<" ";//打印节点 70 visited[v]=true;//标记该节点被访问过 71 queue<int> q;//辅助队列q 72 q.push(v);//将节点v入队 73 while(!q.empty()){//队列不为空 74 int v=q.front();//v为队首元素 75 q.pop();//v出队 76 int w=getFirst(v);//w为节点v的第一个邻接节点 77 while(w!=-1){//v仍有临接节点未访问完 78 if(visited[w]==false){//如果w未被访问,打印节点, 标记该节点被访问过 ,并将该节点入队 79 cout<<(char)(vlist[w]+64)<<" "; 80 visited[w]=true; 81 q.push(w); 82 } 83 w=getNext(v,w);//w重新设置成v的下一个临接节点 84 } 85 } 86 } 87 void print(){//打印图 88 for(int i=0;i<numV;i++){ 89 for(int j=0;j<numV;j++){ 90 if(edge[i][j]==maxValue) 91 cout<<"#"<<" "; 92 else 93 cout<<edge[i][j]<<" "; 94 } 95 cout<<endl; 96 } 97 } 98 private: 99 int *vlist; 100 bool *visited; 101 E **edge; 102 int numV; 103 104 }; 105 //1-9分别对应A-I 106 int main(){ 107 Graph<int> *g=new Graph<int>(10); 108 g->insertE(1,2,1); 109 g->insertE(1,5,1); 110 g->insertE(1,7,1); 111 g->insertE(2,3,1); 112 g->insertE(2,5,1); 113 g->insertE(3,4,1); 114 g->insertE(7,6,1); 115 g->insertE(6,5,1); 116 g->insertE(6,8,1); 117 g->insertE(8,9,1); 118 // g->DFS(1);//利用注释来回切换 119 g->BFS(1); 120 delete g; 121 return 0; 122 }
邻接表法:(时间复杂度n+e),e代表边
1 #include<iostream> 2 #include<queue> 3 #define maxValue 100 4 using namespace std; 5 template<class E> 6 struct e{ 7 int v; 8 e<E> *link; 9 E cost; 10 e(int _v,E w,e *l=NULL){ 11 v=_v; 12 cost=w; 13 link=l; 14 } 15 }; 16 template<class E> 17 struct V{ 18 char data; 19 e<E> *link; 20 V(char d,e<E> *l=NULL){ 21 data=d; 22 link=l; 23 } 24 }; 25 template<class E> 26 class Graph{ 27 public: 28 Graph(int n){ 29 numV=n; 30 vlist=new V<E>*[n]; 31 visited=new bool[n]; 32 for(int i=1;i<n;i++){ 33 vlist[i]=new V<E>(i+64); 34 visited[i]=false; 35 } 36 visited[0]=true; 37 } 38 ~Graph(){ 39 delete[] vlist; 40 } 41 int getFirst(int v){ 42 e<E> *p=vlist[v]->link; 43 if(p!=NULL) 44 return p->v; 45 return -1; 46 } 47 int getNext(int v,int w){ 48 e<E> *p=vlist[v]->link; 49 while(p!=NULL&&p->v!=w){ 50 p=p->link; 51 } 52 if(p!=NULL&&p->link!=NULL){ 53 return p->link->v; 54 } 55 return -1; 56 } 57 E getW(int v1,int v2){ 58 e<E> *p=vlist[v1]->link; 59 while(p!=NULL&&p->v!=v2){ 60 p=p->link; 61 } 62 if(p!=NULL){ 63 return p->cost; 64 } 65 return 0; 66 } 67 bool removeV(int v){ 68 e<E> *p,*q; 69 int k; 70 while(vlist[v]->link!=NULL){ 71 e<E> *m=NULL; 72 p=vlist[v]->link; 73 k=p->v; 74 q=vlist[k]->link; 75 while(q!=NULL&&q->v!=v){ 76 m=q;q=q->link; 77 } 78 if(q!=NULL){ 79 if(m==NULL) vlist[k]->link=q->link; 80 else m->link=q->link; 81 delete q; 82 } 83 vlist[v]->link=p->link; 84 delete p; 85 } 86 return true; 87 } 88 bool insertE(int v1,int v2,int w){ 89 e<E> *p=vlist[v1]->link; 90 e<E> *q; 91 bool isIn=false; 92 while(p!=NULL){ 93 if(p->v==v2){ 94 p->cost=w; 95 isIn=true; 96 break; 97 } 98 p=p->link; 99 } 100 if(isIn){ 101 q=vlist[v2]->link; 102 while(q!=NULL){ 103 if(q->v==v1){ 104 q->cost=w; 105 break; 106 } 107 q=q->link; 108 } 109 return true; 110 }else{ 111 p=new e<E>(v2,w,vlist[v1]->link); 112 vlist[v1]->link=p; 113 q=new e<E>(v1,w,vlist[v2]->link); 114 vlist[v2]->link=q; 115 return true; 116 } 117 return false; 118 } 119 bool removeE(int v1,int v2){ 120 e<E> *p=vlist[v1]->link; 121 e<E> *q=NULL; 122 while(p!=NULL){ 123 if(p->v==v2) 124 break; 125 else{ 126 q=p; 127 p=p->link; 128 } 129 } 130 if(p!=NULL){ 131 if(p==vlist[v1]->link) vlist[v1]->link=p->link; 132 else{ 133 q->link=p->link; 134 delete p; 135 } 136 }else{ 137 return false; 138 } 139 p=vlist[v2]->link; 140 q=NULL; 141 while(p!=NULL){ 142 if(p->v==v1) 143 break; 144 else{ 145 q=p; 146 p=p->link; 147 } 148 } 149 if(p!=NULL){ 150 if(p==vlist[v2]->link) vlist[v2]->link=p->link; 151 else{ 152 q->link=p->link; 153 delete p; 154 } 155 }else{ 156 return false; 157 } 158 } 159 void DFS(int v){ 160 cout<<vlist[v]->data<<" "; 161 visited[v]=true; 162 int w=getFirst(v); 163 while(w!=-1){ 164 if(visited[w]==false) DFS(w); 165 w=getNext(v,w); 166 } 167 } 168 void BFS(int v){ 169 cout<<vlist[v]->data<<" "; 170 visited[v]=true; 171 queue<int> q; 172 q.push(v); 173 while(!q.empty()){ 174 int v=q.front(); 175 q.pop(); 176 int w=getFirst(v); 177 while(w!=-1){ 178 if(visited[w]==false){ 179 cout<<vlist[w]->data<<" "; 180 visited[w]=true; 181 q.push(w); 182 } 183 w=getNext(v,w); 184 } 185 } 186 } 187 void print(){//打印邻接表 188 for(int i=0;i<numV;i++){ 189 cout<<vlist[i]->data<<"->"; 190 e<E> *p=vlist[i]->link; 191 while(p!=NULL){ 192 cout<<p->v<<" "<<p->cost<<"->"; 193 p=p->link; 194 } 195 cout<<"^"<<endl; 196 } 197 } 198 private: 199 V<E> **vlist; 200 bool *visited; 201 int numV; 202 }; 203 int main(){ 204 Graph<int> *g=new Graph<int>(10); 205 g->insertE(1,2,1); 206 g->insertE(1,5,1); 207 g->insertE(1,7,1); 208 g->insertE(2,3,1); 209 g->insertE(2,5,1); 210 g->insertE(3,4,1); 211 g->insertE(7,6,1); 212 g->insertE(6,5,1); 213 g->insertE(6,8,1); 214 g->insertE(8,9,1); 215 // g->DFS(1); 216 g->BFS(1); 217 delete g; 218 return 0; 219 }
标签:没有 顶点 广度 ted 复杂度 遍历 入队 元素 .com
原文地址:http://www.cnblogs.com/ytz1996/p/6390350.html