标签:border 导致 统计量 mpi 矛盾 实例 summary uniq 纯粹
在数据挖掘的过程中,数据预处理占到了整个过程的60%
脏数据:指一般不符合要求,以及不能直接进行相应分析的数据
脏数据包括:缺失值、异常值、不一致的值、重复数据及含有特殊符号(如#、¥、*)的数据
数据清洗:删除原始数据集中的无关数据、重复数据、平滑噪声数据、处理缺失值、异常值等
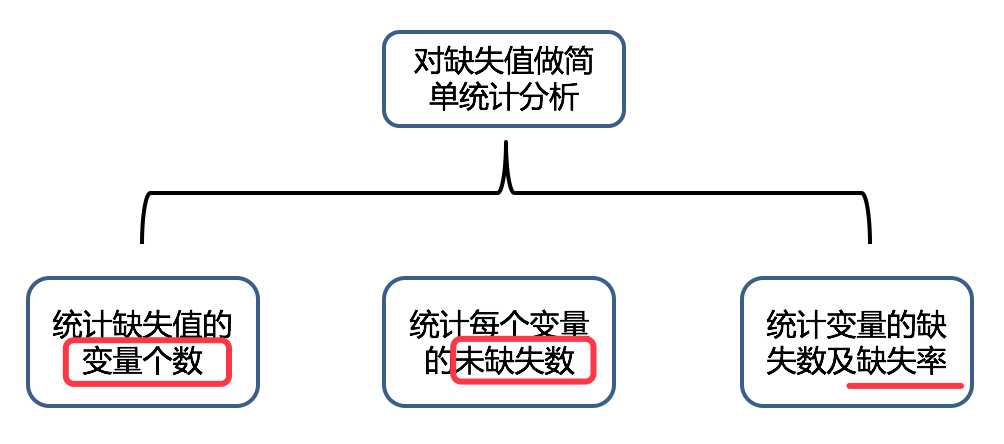
缺失值处理:删除记录、数据插补和不处理

主要用到VIM和mice包
install.packages(c("VIM","mice"))
1.处理缺失值的步骤
步骤:
(1)识别缺失数据;
(2)检查导致数据缺失的原因;
(3)删除包含缺失值的实例或用合理的数值代替(插补)缺失值
缺失值数据的分类:
(1)完全随机缺失:若某变量的缺失数据与其他任何观测或未观测变量都不相关,则数据为完全随机缺失(MCAR)。
(2)随机缺失:若某变量上的缺失数据与其他观测变量相关,与它自己的未观测值不相关,则数据为随机缺失(MAR)。
(3)非随机缺失:若缺失数据不属于MCAR或MAR,则数据为非随机缺失(NIMAR)。
2.识别缺失值
NA:代表缺失值;
NaN:代表不可能的值;
Inf:代表正无穷;
-Inf:代表负无穷。
is.na():识别缺失值;
is.nan():识别不可能值;
is.infinite():无穷值。
is.na()、is.nan()和is.infinte()函数的返回值示例
|
x |
is.na(x) |
is.nan(x) |
is.infinite(x) |
|
x<-NA |
TRUE |
FALSE |
FALSE |
|
x<-0/0 |
TRUE |
TRUE |
FALSE |
|
x<-1/0 |
FALSE |
FALSE |
TRUE |
|
|
|
|
|
complete.cases()可用来识别矩阵或数据框中没有缺失值的行,若每行都包含完整的实例,则返回TRUE的逻辑向量,若每行有一个或多个缺失值,则返回FALSE;
3.探索缺失值模式
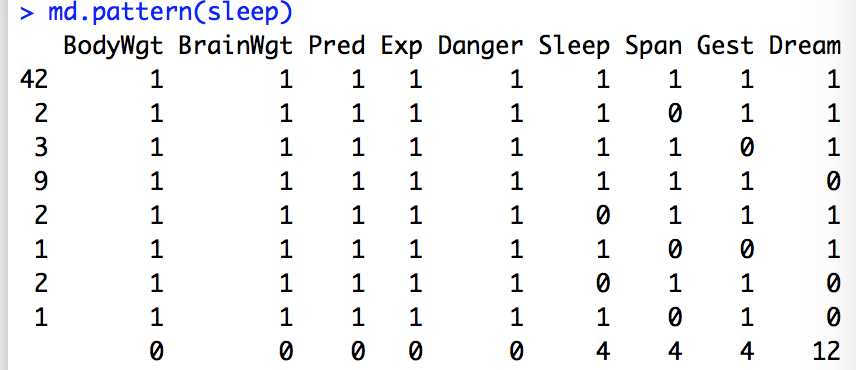
(1)列表显示缺失值
mice包中的md.pattern()函数可以生成一个以矩阵或数据框形式展示缺失值模式的表格
library(mice)
data(sleep,package="VIM")
md.pattern(sleep)
(2)图形探究缺失数据
VIM包中提供大量能可视化数据集中缺失值模式的函数:aggr()、matrixplot()、scattMiss()
library("VIM")
aggr(sleep,prop=FALSE,numbers=TRUE)
library("VIM")
aggr(sleep,prop=TRUE,numbers=TRUE)#用比例代替了计数
matrixplot()函数可生成展示每个实例数据的图形
matrixplot(sleep)
浅色表示值小,深色表示值大;默认缺失值为红色。
marginplot()函数可生成一幅散点图,在图形边界展示两个变量的缺失值信息。
library("VIM")
marginplot(sleep[c("Gest","Dream")],pch=c(20),col=c("darkgray","red","blue"))
(3)用相关性探索缺失值
影子矩阵:用指示变量替代数据集中的数据(1表示缺失,0表示存在),这样生成的矩阵有时称作影子矩阵。
求这些指示变量间和它们与初始(可观测)变量间的相关性,有且于观察哪些变量常一起缺失,以及分析变量“缺失”与其他变量间的关系。
head(sleep)
str(sleep)
x<-as.data.frame(abs(is.na(sleep)))
head(sleep,n=5)
head(x,n=5)
y<-x[which(sd(x)>0)]
cor(y)
cor(sleep,y,use="pairwise.complete.obs")
4.理解缺失值数据的来由和影响
识别缺失数据的数目、分布和模式有两个目的:
(1)分析生成缺失数据的潜在机制;
(2)评价缺失数据对回答实质性问题的影响。
即:
(1)缺失数据的比例有多大?
(2)缺失数据是否集中在少数几个变量上,抑或广泛存在?
(3)缺失是随机产生的吗?
(4)缺失数据间的相关性或与可观测数据间的相关性,是否可以表明产生缺失值的机制呢?
若缺失数据集中在几个相对不太重要的变量上,则可以删除这些变量,然后再进行正常的数据分析;
若有一小部分数据随机分布在整个数据集中(MCAR),则可以分析数据完整的实例,这样仍可得到可靠有效的结果;
若以假定数据是MCAR或MAR,则可以应用多重插补法来获得有铲的结论。
若数据是NMAR,则需要借助专门的方法,收集新数据,或加入一个相对更容易、更有收益的行业。
5.理性处理不完整数据
6.完整实例分析(行删除)
函数complete.cases()、na.omit()可用来存储没有缺失值的数据框或矩阵形式的实例(行):
newdata<-mydata[complete.cases(mydata),]
newdata<-na.omit(mydata)
options(digits=1)
cor(na.omit(sleep))
cor(sleep,use="complete.obs")
fit<-lm(Dream~Span+Gest,data=na.omit(sleep))
summary(fit)
7.多重插补
多重插补(MI)是一种基于重复模拟的处理缺失值的方法。
MI从一个包含缺失值的数据集中生成一组完整的数据集。每个模拟数据集中,缺失数据将使用蒙特卡洛方法来填补。
此时,标准的统计方法便可应用到每个模拟的数据集上,通过组合输出结果给出估计的结果,以及引入缺失值时的置信敬意。
可用到的包Amelia、mice和mi包
mice()函数首先从一个包含缺失数据的数据框开始,然后返回一个包含多个完整数据集的对象。每个完整数据集都是通过对原始数据框中的缺失数据进行插而生成的。
with()函数可依次对每个完整数据集应用统计模型
pool()函数将这些单独的分析结果整合为一组结果。
最终模型的标准误和p值都将准确地反映出由于缺失值和多重插补而产生的不确定性。
基于mice包的分析通常符合以下分析过程:
library(mice)
imp<-mice(mydata,m)
fit<-with(imp,analysis)
pooled<-pool(fit)
summary(pooled)
mydata是一个饮食缺失值的矩阵或数据框;imp是一个包含m个插补数据集的列表对象,同时还含有完成插补过程的信息,默认的m=5analysis是一个表达式对象,用来设定应用于m个插补的统计分析方法。方法包括做线回归模型的lm()函数、做广义线性模型的glm()函数、做广义可加模型的gam()、及做负二项模型的nbrm()函数。fit是一个包含m个单独统计分析结果的列表对象;pooled是一个包含这m个统计分析平均结果的列表对象。</pre><pre name="code" class="plain">library(mice)
data(sleep,package="VIM")
imp<-mice(sleep,seed=1234)
fit<-with(imp,lm(Dream~Span+Gest))
pooled<-pool(fit)
summary(pooled)
impimp$imp$Dream
利用complete()函数可观察m个插补数据集中的任意一个,格式为:complete(imp,action=#)
eg:
dataset3<-complete(imp,action=3)
dataset3
8.处理缺失值的其他方法
|
软件包 |
描述 |
|
Hmisc |
包含多种函数,支持简单插补、多重插补和典型变量插补 |
|
mvnmle |
对多元正态颁数据中缺失值的最大似然估计 |
|
cat |
对数线性模型中多元类别型变量的多重插补 |
|
arrayImpute\arraryMissPattern、SeqKnn |
处理微阵列缺失值数据的实用函数 |
|
longitudinalData |
相关的函数列表,比如对时间序列缺失值进行插补的一系列函数 |
|
kmi |
处理生存分析缺失值的Kaplan-Meier多重插补 |
|
mix |
一般位置模型中混合类别型和连续型数据的多重插补 |
|
pan |
多元面板数据或聚类的多重插补 |
(1)成对删除
处理含缺失值的数据集时,成对删除常作为行删除的备选方法使用。对于成对删除,观测只是当它含缺失数据的变量涉及某个特定分析时才会被删除。
cor(sleep,use="pairwise.complete.obs")
虽然成对删除似乎利用了所有可用数据,但实际上每次计算只用了不同的数据集,这将会导致一些扭曲,故建议不要使用该方法。
(2)简单(非随机)插补
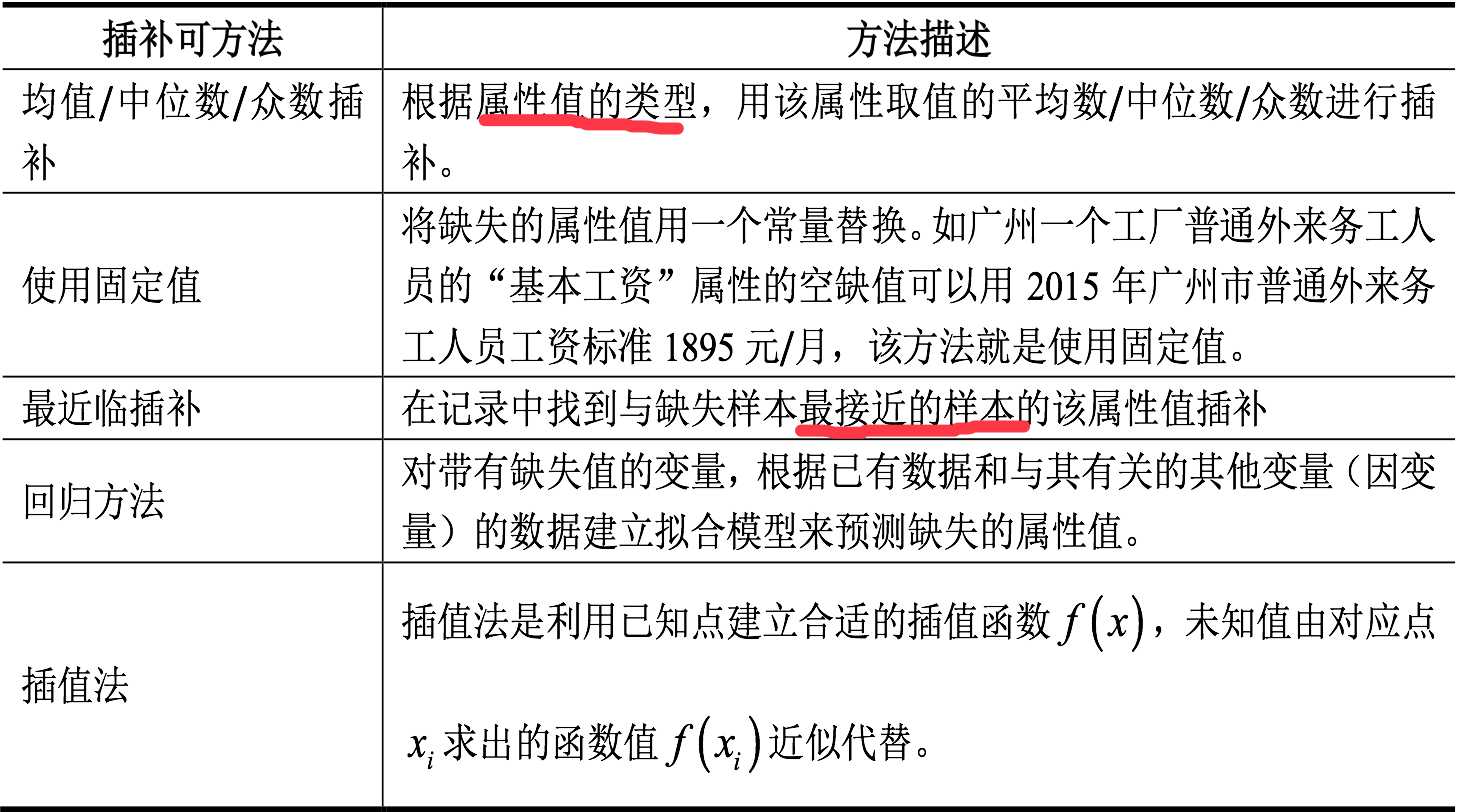
简单插补,即用某个值(如均值、中位数或众数)来替换变量中的缺失值。注意,替换是非随机的,这意味着不会引入随机误差(与多重衬托不同)。
简单插补的一个优点是,解决“缺失值问题”时不会减少分析过程中可用的样本量。虽然 简单插补用法简单,但对于非MCAR的数据会产生有偏的结果。若缺失数据的数目非常大,那么简单插补很可能会低估标准差、曲解变量间的相关性,并会生成不正确的统计检验的p值。应尽量避免使用该方法。
----------------------------------------------------------------
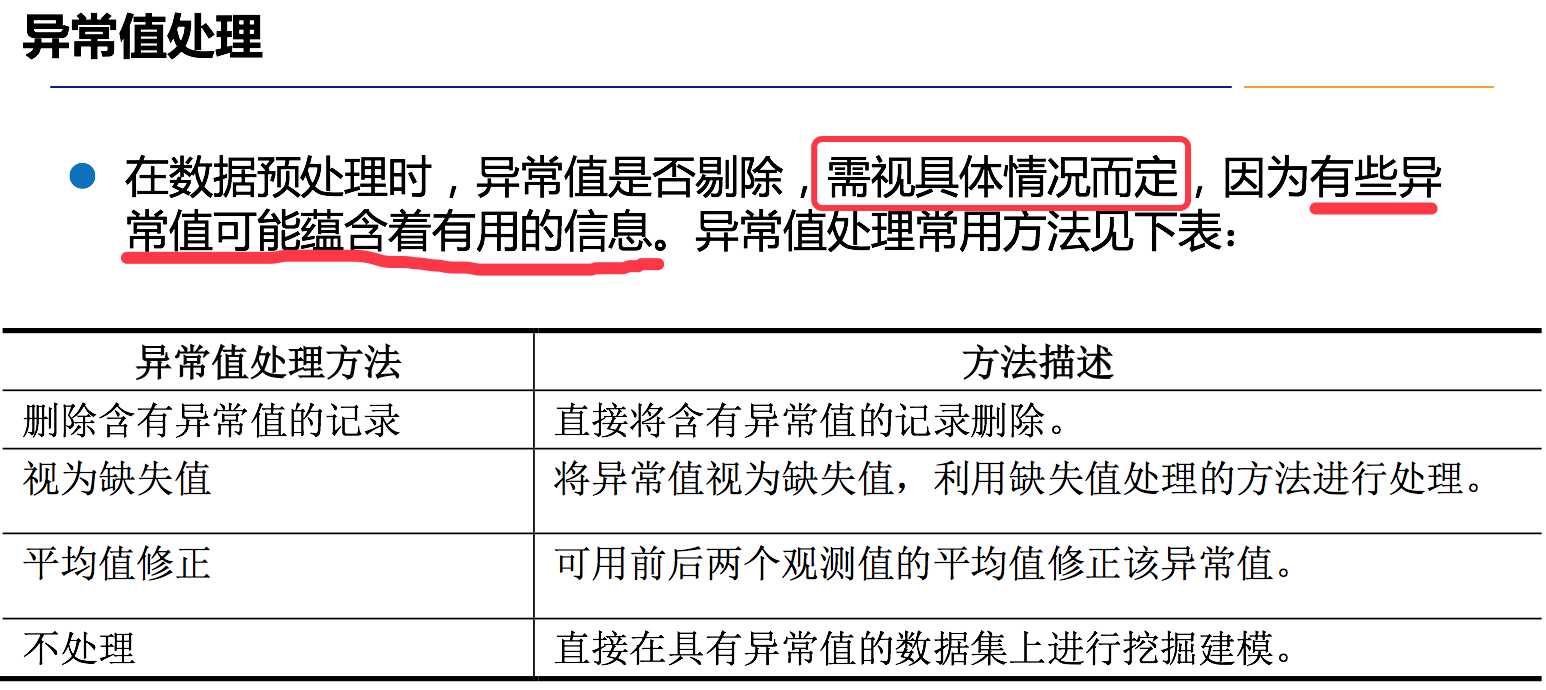
异常值分析是检验数据是否有录入错误以及含有不合常理的数据;
异常值是指样本中的个别值,其数据明显偏离其余的观测值。异常值也称为离群点,异常值的分析也称为离群点分析。
异常值处理一般分为以下几个步骤:异常值检测、异常值筛选、异常值处理。
其中异常值检测的方法主要有:箱型图、简单统计量(比如观察极(大/小)值),3σ原则 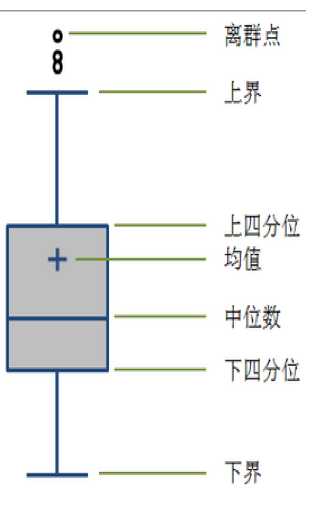
异常值处理方法主要有:删除法、插补法、替换法。
数据不一致:指数据的矛盾性、不相容性;在数据挖掘过程中,不一致数据的产生主要发生在数据集成的过程中,可能是由于被挖掘数据是来自于从不同的数据源、重复存放的数据未能进行一致性地更新造成的。
下面主要是进行异常值检验、离群点分析、异常值处理:
提到异常值不得不说一个词:鲁棒性。就是不受异常值影响,一般是鲁棒性高的数据,比较优质。
一、异常值检验
异常值大概包括缺失值、离群值、重复值,数据不一致。
summary可以显示每个变量的缺失值数量.
关于缺失值的检测应该包括:缺失值数量、缺失值比例、缺失值与完整值数据筛选。
#缺失值解决方案
sum(complete.cases(saledata)) #is.na(saledata)
sum(!complete.cases(saledata))
mean(!complete.cases(saledata)) #1/201数字,缺失值比例
saledata[!complete.cases(saledata),] #筛选出缺失值的数值
箱型图的检测包括:四分位数检测(箱型图自带)+1δ标准差上下+异常值数据点。
箱型图有一个非常好的地方是,boxplot之后,结果中会自带异常值,就是下面代码中的sp$out,这个是做箱型图,按照上下边界之外为异常值进行判定的。
上下边界,分别是Q3+(Q3-Q1)、Q1-(Q3-Q1)。
sp=boxplot(saledata$"销量",boxwex=0.7)
title("销量异常值检测箱线图")
xi=1.1
sd.s=sd(saledata[complete.cases(saledata),]$"销量")
mn.s=mean(saledata[complete.cases(saledata),]$"销量")
points(xi,mn.s,col="red",pch=18)
arrows(xi, mn.s - sd.s, xi, mn.s + sd.s, code = 3, col = "pink", angle = 75, length = .1)
text(rep(c(1.05,1.05,0.95,0.95),length=length(sp$out)),labels=sp$out[order(sp$out)],
sp$out[order(sp$out)]+rep(c(150,-150,150,-150),length=length(sp$out)),col="red")
代码中text函数的格式为text(x,label,y,col);points加入均值点;arrows加入均值上下1δ标准差范围箭头。
箱型图还有等宽与等深分箱法
数据去重与数据分组合并存在一定区别,去重是纯粹的所有变量都是重复的,而数据分组合并可能是因为一些主键的重复。
数据去重包括重复检测(table、unique函数)以及重复数据处理(unique/duplicated)。
常见的有unique、数据框中duplicated函数,duplicated返回的是逻辑值。
常见的异常值处理办法是删除法、替代法(连续变量均值替代、离散变量用众数以及中位数替代)、插补法(回归插补、多重插补)
除了直接删除,可以先把异常值变成缺失值、然后进行后续缺失值补齐。
实践中,异常值处理,一般划分为NA缺失值或者返回公司进行数据修整(数据返修为主要方法)
利用图形——箱型图进行异常值检测。
#异常值识别
par(mfrow=c(1,2))#将绘图窗口划为1行两列,同时显示两图
dotchart(inputfile$sales)#绘制单变量散点图,多兰图
pc=boxplot(inputfile$sales,horizontal=T)#绘制水平箱形图
代码来自《R语言数据分析与挖掘实战》第四节。
整行替换数据框里99%以上和1%以下的点,将99%以上的点值=99%的点值;小于1%的点值=1%的点值。
(本图来自CDA DSC,L2-R语言课程,常老师所述)
#异常数据处理
q1<-quantile(result$tot_derog, 0.001) #取得时1%时的变量值
q99<-quantile(result$tot_derog, 0.999) #replacement has 1 row, data has 0 说明一个没换
result[result$tot_derog<q1,]$tot_derog<-q1
result[result$tot_derog>q99,]$tot_derog<-q99
summary(result$tot_derog) #盖帽法之后,查看数据情况
fix(inputfile)#表格形式呈现数据
which(inputfile$sales==6607.4)#可以找到极值点序号(位置)是啥
把缺失值数据集、非缺失值数据集分开。
#缺失值的处理
inputfile$date=as.numeric(inputfile$date)#将日期转换成数值型变量
sub=which(is.na(inputfile$sales))#识别缺失值所在行数
inputfile1=inputfile[-sub,]#将数据集分成完整数据和缺失数据两部分
inputfile2=inputfile[sub,]
将连续变量等级化之后,不同的分位数的数据就会变成不同的等级数据,连续变量离散化了,消除了极值的影响。
数据集分为缺失值、非缺失值两块内容。缺失值处理如果是连续变量,可以选择均值;离散变量,可以选择众数或者中位数。
计算非缺失值数据的均值,
然后赋值给缺失值数据。
#均值替换法处理缺失,结果转存
#思路:拆成两份,把缺失值一份用均值赋值,然后重新合起来
avg_sales=mean(inputfile1$sales)#求变量未缺失部分的均值
inputfile2$sales=rep(avg_sales,n)#用均值替换缺失
result2=rbind(inputfile1,inputfile2)#并入完成插补的数据
#回归插补法处理缺失,结果转存
model=lm(sales~date,data=inputfile1)#回归模型拟合
inputfile2$sales=predict(model,inputfile2)#模型预测
result3=rbind(inputfile1,inputfile2)
注意:多重插补的处理有两个要点:先删除Y变量的缺失值然后插补
1、被解释变量有缺失值的观测不能填补,只能删除,不能自己乱补;
2、只对放入模型的解释变量进行插补。
比较详细的来介绍一下这个多重插补法。笔者整理了大致的步骤简介如下:
缺失数据集——MCMC估计插补成几个数据集——每个数据集进行插补建模(glm、lm模型)——将这些模型整合到一起(pool)——评价插补模型优劣(模型系数的t统计量)——输出完整数据集(compute)
步骤详细介绍:
函数mice()首先从一个包含缺失数据的数据框开始,然后返回一个包含多个(默认为5个)完整数据集的对象。
每个完整数据集都是通过对原始数据框中的缺失数据进行插补而生成的。 由于插补有随机的成分,因此每个完整数据集都略有不同。
其中,mice中使用决策树cart有以下几个要注意的地方:该方法只对数值变量进行插补,分类变量的缺失值保留,cart插补法一般不超过5k数据集。
然后, with()函数可依次对每个完整数据集应用统计模型(如线性模型或广义线性模型) ,
最后, pool()函数将这些单独的分析结果整合为一组结果。最终模型的标准误和p值都将准确地反映出由于缺失值和多重插补而产生的不确定性。
#多重插补法处理缺失,结果转存
library(lattice) #调入函数包
library(MASS)
library(nnet)
library(mice) #前三个包是mice的基础
imp=mice(inputfile,m=4) #4重插补,即生成4个无缺失数据集
fit=with(imp,lm(sales~date,data=inputfile))#选择插补模型
pooled=pool(fit)
summary(pooled)
result4=complete(imp,action=3)#选择第三个插补数据集作为结果
结果解读:
(1)imp对象中,包含了:每个变量缺失值个数信息、每个变量插补方式(PMM,预测均值法常见)、插补的变量有哪些、预测变量矩阵(在矩阵中,行代表插补变量,列代表为插补提供信息的变量, 1和0分别表示使用和未使用);
同时 利用这个代码imp$imp$sales 可以找到,每个插补数据集缺失值位置的数据补齐具体数值是啥。
(2)with对象。插补模型可以多样化,比如lm,glm都是可以直接应用进去,详情可见《R语言实战》第十五章;
(3)pool对象。summary之后,会出现lm模型系数,可以如果出现系数不显著,那么则需要考虑换插补模型;
(4)complete对象。m个完整插补数据集,同时可以利用此函数输出。
其他:
mice包提供了一个很好的函数md.pattern(),用它可以对缺失数据的模式有个更好的理解。还有一些可视化的界面,通过VIM、箱型图、lattice来展示缺失值情况。可见博客:在R中填充缺失数据—mice包
离群点检测与异常值主要的区别在于:
异常值针对单一变量,而离群值指的是很多变量综合考虑之后的异常值。
下面介绍一种基于聚类+欧氏距离的离群点检测方法。
基于聚类的离群点检测的步骤如下:数据标准化——聚类——求每一类每一指标的均值点——每一类每一指标生成一个矩阵——计算欧式距离——画图判断。
Data=read.csv(".data.csv",header=T)[,2:4]
Data=scale(Data)
set.seed(12)
km=kmeans(Data,center=3)
print(km)
km$centers #每一类的均值点
#各样本欧氏距离,每一行
x1=matrix(km$centers[1,], nrow = 940, ncol =3 , byrow = T)
juli1=sqrt(rowSums((Data-x1)^2))
x2=matrix(km$centers[2,], nrow = 940, ncol =3 , byrow = T)
juli2=sqrt(rowSums((Data-x2)^2))
x3=matrix(km$centers[3,], nrow = 940, ncol =3 , byrow = T)
juli3=sqrt(rowSums((Data-x3)^2))
dist=data.frame(juli1,juli2,juli3)
##欧氏距离最小值
y=apply(dist, 1, min)
plot(1:940,y,xlim=c(0,940),xlab="样本点",ylab="欧氏距离")
points(which(y>2.5),y[which(y>2.5)],pch=19,col="red")
参考来源于:
https://kknews.cc/zh-cn/tech/e2v4z.html
http://blog.csdn.net/sinat_26917383/article/details/51210793
标签:border 导致 统计量 mpi 矛盾 实例 summary uniq 纯粹
原文地址:http://www.cnblogs.com/nxld/p/6477001.html