标签：最优 完全 构建 .com 技术 局部最优 有向无环图 避免 期望
该文章参考周志华老师著的《机器学习》一书
1. 朴素贝叶斯分类器
朴素贝叶斯分类器采用了“属性条件独立性假设”：对已知类别，假设所有属性相互独立，即假设每个属性独立的对分类结果发生影响。
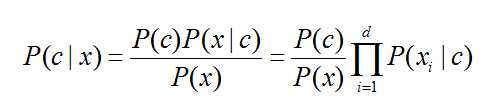d为属性数目，xi 为 x 在第 i 个属性上的取值，朴素贝叶斯分类器的表达式为：
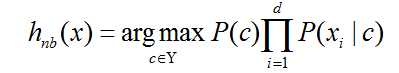
令 Dc 表示训练集 D 中第 c 类样本的集合，例如西瓜数据集有两个类别：好瓜和坏瓜，若有充足的独立同分布样本，则
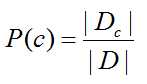对于离散属性：
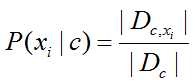，Dc,xi 表示 Dc 在第 i 个属性上取值为 xi 的样本组成的集合；对于连续属性考虑连续密度函数，假定 p(xi|c) 服从正态分布。
为了避免其他属性携带的信息被训练集中未出现的属性抹去，在估计概率值时通常要进行平滑。N 表示训练集 D 中可能的类别数，Ni 表示第 i 个属性可能的取值数：
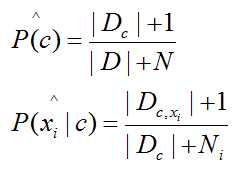
2. 半朴素贝叶斯分类器
放松独立性条件，适当考虑一部分属性间的相互依赖信息，“独依赖估计”（简称ODE）是半朴素贝叶斯分类器常用的一种策略。主要有三种方法：
（1）SPODE（超父独依赖估计），假设所有的属性都依赖于同一个属性，最后类别结点和每个属性都连接起来；
（2）TAN（Tree Augmented naive Bayes），在最大带权树的基础上，步骤如下：计算两个属性之间的互信息；以属性为结点构建完全图，任意两个结点之间的边的权重设为互信息；构建次完全图的最大带权生成树，挑选根变量，将边置为有向；加入类别结点y，增加从y 到每个属性的有向边。
（3）AODE（平均独依赖估计），尝试将每个属性作为超父来构建SPOE，集成结果，与朴素贝叶斯相似，无需模型选择，是对符合条件的样本计数。
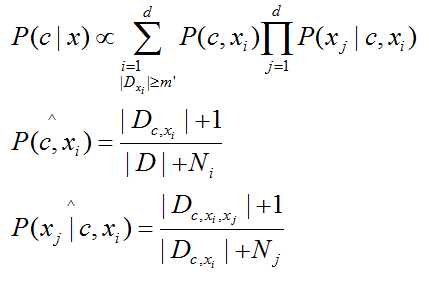
3. 贝叶斯网
简称“信念网”，借助有向无环图（DAG）来刻画属性之间的依赖关系
4. EM算法
前面的讨论假设样本所有属性变量的值都已被观测到，但在现实应用中训练样本很难是完整的，所以会存在未观测到的变量，即“隐变量”，所以用到EM（期望最大化）算法：第一步是期望（E）步，利用当前估计的参数值来计算对数似然的期望值（即最优隐变量的值）；第二步是最大化（M）步，寻找能使E步产生的似然期望最大化的参数值。然后交替下去，直至收敛到局部最优解。可看作是坐标下降法。
标签：最优 完全 构建 .com 技术 局部最优 有向无环图 避免 期望
原文地址：http://www.cnblogs.com/rgly/p/6511918.html
