标签:sort 时间复杂度 数字 1.2 image 稳定性 imp out 操作
一、简单选择排序和堆排序都属于选择排序
选择排序的思想是:每一趟从待排序的记录中选出关键字最小的记录,按顺序放在以排序的记录序列的后面,知道全部拍完为止。
二、简单选择排序(直接选择排序)
1.简单选择排序法是每次循环找出最值,循环结束后将最值调整到合适位置,交换的次数少。
每次找出当前无序队列中的最小的元素与第一个交换位置,再选择第二小的与第二个交换位置
原始队列: 3 5 6 2 4 1(最小元素1与3交换)
第一步: 1 5 6 2 4 3 (当前最小元素2与5交换)
第二步: 1 2 6 5 4 3 (当前最小元素3与6交换)
第三步: 1 2 3 5 4 6 (当前最小元素4与5交换)
第四步: 1 2 3 4 5 6
第五步: 1 2 3 4 5 6
第六步: 1 2 3 4 5 6
2.时间复杂度
最好情况(正序)不移动
最坏情况(逆序)移动3(n-1)次
平均时间复杂度O(n*n)
空间复杂度O(1)
具体时间复杂度等分析,请参考:http://www.cnblogs.com/zhangxue521/p/6533134.html
3.算法特点
①稳定排序
②可用于链式存储结构
③移动记录次数较少,当每一记录占用空间较多时,此方法比直接插入排序快
4.java代码

1 import java.util.Scanner; 2 3 public class _2简单选择排序 { 4 public static void main(String[] args) { 5 int a[] = new int[6]; 6 Scanner scanner = new Scanner(System.in); 7 for (int i = 0; i < a.length; i++) { 8 a[i] = scanner.nextInt(); 9 } 10 for (int i = 0; i < a.length; i++) { 11 int min = i; 12 // 循环找当前队列中的最小的数字,将min标志赋予它 13 for (int j =i+1; j < a.length; j++) { 14 if ( a[j]<a[min] ) { 15 min = j; 16 } 17 } 18 //交换最小值到当前无序队列的最前面 19 if (min!=i) { 20 int temp = a[i]; 21 a[i] = a[min]; 22 a[min] = temp; 23 } 24 for (int m : a) { 25 System.out.print(m+" "); 26 } 27 System.out.println(); 28 } 29 } 30 }
三、堆排序
1.堆排序是一种树形选择排序,在排序过程中,将待排序的记录r[1..n]看成是一棵完全二叉树的顺序存储结构,利用完全二叉树的双亲结点和孩子结点之间的内在关系,在当前无序的序列中选择关键字最大(或者最小的)记录
1.1、先将无序队列,列成二叉树的的样子
1.2、建初堆。从n/2向上取整处开始调整,当前节点数字一定要大于(小于)左右两孩子,n/2--,一直向上若最后排序结果是升序就调整成大顶堆,若是降序就调整成小顶堆
1.3、开始排序,将堆顶元素和最后一个元素互换位置,换下来的即可以依次加入有序队列,交换完成后继续进行第二步操作,调整堆
1.4、然后再进行交换(注意:上面交换下来的已经是排好序的,不用进行调整,即忽略交换下来的数字即可)
由于堆排序的过程图画着不太方便,就上传了数据结构课本上的堆排序过程,这个比较过程比较详细
建初堆:
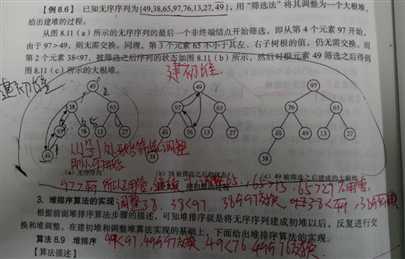
堆排序调整堆
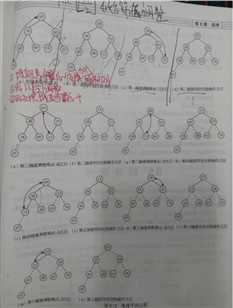
2.时间复杂度
堆排序的时间主要耗费在建初堆和调整堆时进行的反复“筛选”上
设有n个记录的初始序列所对应的完全二叉树的深度为h,建处堆时,每个非终端节点都要自上而下进行“筛选”,由于第i层上的节点小于等于2的i-1次方,。。。。。。
堆排序最坏的情况下时间复杂度也是O(nlog2n)
空间复杂度O(1)
具体时间复杂度等分析,请参考:http://www.cnblogs.com/zhangxue521/p/6533134.html
3.算法特点
①具有不稳定性
②只能用于顺序结构,不能用于链式结构
③建初堆时所需的比较次数比较多,因此记录数较少时不宜采用。堆排序在最坏的情况下的时间复杂度为O(nlog2n),因此当记录较多时比较高效
4.java代码

1 public class _4堆排序 { 2 public static void main(String[] args) { 3 _4堆排序 hs = new _4堆排序(); 4 int[] array = {87,45,78,32,17,65,53,9,122}; 5 System.out.print("构建大根堆:"); 6 hs.toString(hs.buildMaxHeap(array)); 7 System.out.print("\n"+"删除堆顶元素:"); 8 hs.toString(hs.deleteMax(array)); 9 System.out.print("\n"+"插入元素63:"); 10 hs.toString(hs.insertData(array, 63)); 11 System.out.print("\n"+"大根堆排序:"); 12 hs.toString(hs.heapSort(array)); 13 } 14 //输出 15 public void toString(int[] array){ 16 for(int i:array){ 17 System.out.print(i+" "); 18 } 19 } 20 //构建大根堆:将array看成完全二叉树的顺序存储结构 21 private int[] buildMaxHeap(int[] array){ 22 //即从中间元素开始调整 23 //从最后一个节点array.length-1的父节点(array.length-1-1)/2开始,直到根节点0,反复调整堆 24 for(int i=(array.length-2)/2;i>=0;i--){ 25 adjustDownToUp(array, i,array.length); 26 } 27 return array; 28 } 29 30 //将元素array[k]自下往上逐步调整树形结构 31 private void adjustDownToUp(int[] array,int k,int length){ 32 int temp = array[k]; 33 for(int i=2*k+1; i<length-1; i=2*i+1){ //i为初始化为节点k的左孩子,沿节点较大的子节点向下调整 34 if(i<length && array[i]<array[i+1]){ //取节点较大的子节点的下标 35 i++; //如果节点的右孩子>左孩子,则取右孩子节点的下标 36 } 37 if(temp>=array[i]){ //根节点 >=左右子女中关键字较大者,调整结束 38 break; 39 }else{ //根节点 <左右子女中关键字较大者 40 array[k] = array[i]; //将左右子结点中较大值array[i]调整到双亲节点上 41 k = i; //【关键】修改k值,以便继续向下调整 42 } 43 } 44 array[k] = temp; //被调整的结点的值放人最终位置 45 } 46 47 //堆排序 48 public int[] heapSort(int[] array){ 49 array = buildMaxHeap(array); //初始建堆,array[0]为第一趟值最大的元素 50 for(int i=array.length-1;i>1;i--){ 51 int temp = array[0]; //将堆顶元素和堆低元素交换,即得到当前最大元素正确的排序位置 52 array[0] = array[i]; 53 array[i] = temp; 54 adjustDownToUp(array, 0,i); //整理,将剩余的元素整理成堆 55 } 56 return array; 57 } 58 59 //删除堆顶元素操作 60 public int[] deleteMax(int[] array){ 61 //将堆的最后一个元素与堆顶元素交换,堆底元素值设为-99999 62 array[0] = array[array.length-1]; 63 array[array.length-1] = -99999; 64 //对此时的根节点进行向下调整 65 adjustDownToUp(array, 0, array.length); 66 return array; 67 } 68 69 //插入操作:向大根堆array中插入数据data 70 public int[] insertData(int[] array, int data){ 71 array[array.length-1] = data; //将新节点放在堆的末端 72 int k = array.length-1; //需要调整的节点 73 int parent = (k-1)/2; //双亲节点 74 while(parent >=0 && data>array[parent]){ 75 array[k] = array[parent]; //双亲节点下调 76 k = parent; 77 if(parent != 0){ 78 parent = (parent-1)/2; //继续向上比较 79 }else{ //根节点已调整完毕,跳出循环 80 break; 81 } 82 } 83 array[k] = data; //将插入的结点放到正确的位置 84 return array; 85 } 86 87 }
标签:sort 时间复杂度 数字 1.2 image 稳定性 imp out 操作
原文地址:http://www.cnblogs.com/zhangxue521/p/6534210.html