标签:log mem ott return last maxsize contract 奇数 cmd
1. 什么是树状数组?
假设C [i]表示这个数据结构的第i个元素, A [i]表示第i数的数值。
C [i] = A [i] ( i 为奇数)
C [i] = A [k] + .. + A [i]; (k 等于 i的二进制最后一位1去掉 + 1, i为偶数)
看图, 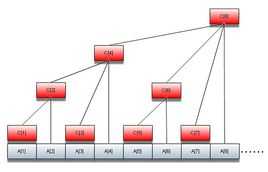
2. 想法
感觉这是某个理论的衍生物,或者是多个理论的杂交物。
3. 应用
经常用在对紧挨着的大量的数字进行相加, 而且其中会修改某一位数字, 其时间复杂度 logn.
4. 我用它解决这个问题(附上代码)
南将军手下有N个士兵,分别编号1到N,这些士兵的杀敌数都是已知的。
小工是南将军手下的军师,南将军经常想知道第m号到第n号士兵的总杀敌数,请你帮助小工来回答南将军吧。
南将军的某次询问之后士兵i可能又杀敌q人,之后南将军再询问的时候,需要考虑到新增的杀敌数。

#include <stdio.h> #include <stdlib.h> #include <string.h> #define MAX_SIZE 1000000 #define CMD_MAX_SIZE 10 int c [MAX_SIZE + 1] = {0}; //树状数组 int a [MAX_SIZE + 1] = {0}; int main(void) { int N,M; int temp; int sum = 0; int i, j; char cmdStr [CMD_MAX_SIZE]; int m, n; int GetLast(int value); int GetSum(int n); void AddIt(int index, int value, int maxSize); memset((unsigned char *)c, 0, (MAX_SIZE + 1) * sizeof(int)); //清零 memset((unsigned char *)a, 0, (MAX_SIZE + 1) * sizeof(int)); scanf("%d%d",&N,&M); for(i = 1; i <= N; i ++) //初始化 { scanf("%d", &a [i]); if(i % 2 == 0) { for(j = i - GetLast(i) + 1; j <= i; j ++) { c [i] += a [j]; } } else { c [i] = a [i]; } } while(M --) { fscanf(stdin, "%s %d %d", cmdStr, &m, &n); //或者i和addNum if(!strcmp(cmdStr, "QUERY")) { fprintf(stdout, "%d\n", GetSum(n) - GetSum(m - 1) ); } else if(!strcmp(cmdStr, "ADD")) { AddIt(m, n, N); } else { exit(EXIT_FAILURE); } } return 1; } /* * 获取整数的二进制形式左数最后一个1 * value -- 指定整数 * 返回结果。 */ int GetLast(int value) { return value & (-value); } /* * 获取前n个数的和 * n -- 表示前n个数 * 返回它们的和。 */ int GetSum(int n) { int sum = 0; while(n > 0) { sum += c [n]; n -= GetLast(n); } return sum; } /* * 给某个元素加值 * index -- 指定元素的序号 * value -- 加的数值 * maxSize -- 树状数组的上界 */ void AddIt(int index, int value, int maxSize) { int GetLast(int value); while(index <= maxSize) { c [index] += value; index += GetLast(index); } }
标签:log mem ott return last maxsize contract 奇数 cmd
原文地址:http://www.cnblogs.com/the-one/p/6544212.html