标签:blog 思考 代码 函数 初学 函数调用 遍历 开始 实现
上一次我们从什么是表一直讲到了链表该怎么实现的想法上:http://www.cnblogs.com/mm93/p/6574912.html
而这一次我们就要实现所说的承诺,即实现链表应有的操作(至于游标数组……我决定还是给它单独写个博文比较好~)。
那么,我们的过程应该是怎么样的呢?首先当然是分析需要什么操作,然后再逐一思考该如何实现,最后再以代码的形式写出来。
不难发现,我们希望链表能支持的(基础,可以由此延伸)操作就是:
1.给出第n个元素
2.在第n个元素的后面插入一个元素(包含在最后一个元素后面插入一个元素)
3.删除第n个元素(包含删除第一个元素)
概括而言就是查找、插入、删除。
首先要说一句废话,就是链表不是C语言内置的数据结构,其不能像数组一样使用下标[]来访问某个元素,因此即使是查找我们都得用函数来实现。然后要说明的就是,实际应用中的元素类型可能会很复杂,但为了便于分析与学习,我们假设元素为int型。然后我们将结点的定义也改成如下:
struct node { int data; struct node *next; } typedef struct node * List; //List用于指向第一个结点,表示链表的“头” typedef struct node * Node;//Node用于指向某个结点
现在,我们可以开始第二步,逐一思考各操作该如何实现了。
对于查找操作,如果是数组会很简单,因为数组支持下标操作,想要数组a的第n个元素只需要用a[n-1]即可,但是链表的实现则稍稍麻烦一点,当然也只是稍稍罢了:-P。
回顾链表的实现思路,我们发现其关键点是“每个元素都记住了下一个元素的位置”,并且我们手上掌握的就只有第一个结点(从今以后,原数据我们称为元素,带有指针的“封装”的元素我们称为结点)的位置,即List存储的地址(我们不再介绍背景,直接搬用(4)中的代码背景)。那么根据这两点,我们理应想到找到第n个元素的办法,那就是“从第一个结点开始一个一个找,直到第n个结点时返回其元素”。那么这句话中的“找”,显然就是利用结点中的next指针了。
好了,提示就给到这儿,我们接下来直接给出实现查找的代码:
1 int Find ( List L,int N ) 2 { 3 Node temp=L; 4 for( int i=1;i<N ;++i )//循环次数这里稍稍注意一下 5 temp=temp->next; //我们需要“找下一个”找n-1次而不是n次 6 7 return temp->data; 8 }
显然,这段代码是不完善的,或者专业点说是不健壮的。所谓健壮的代码,就是指要能够处理各种边界(或者说极端)条件,给出错误或提示或不允许执行等。而我们这段代码中不健壮的地方体现在哪呢?
1.没有考虑L为NULL的情况
2.没有考虑N<1或者N大于L中元素个数的情况
3.没有在参数列表中使用const修饰L来防止无意的修改(也给调用者一个安心:-P)
等等
如果要令这个Find函数更加健壮,显然我们需要考虑上述情况,并且需要利用某些手段来给出错误提示,比如接收一个额外的指针参数,函数调用之后该指针所指数据中会存储着本次调用的情况。不过这都是另外的话题了,我们还是先不考虑这些。我们写的代码目前的主要目的是说明如何实现我们想要的操作,或者说操作的核心(因为Find操作也理应考虑某些边界情况)。
好了,绕了一个圈子,现在我们回归到链表的讨论上。接下来我们要考虑的是链表的插入操作(删除操作的基础是插入操作,so)。
对于插入操作,好吧,我们不得不又绕个小圈子。那就是链表的插入和数组的插入有何不同呢?
对于数组来说,如果要想在第n-1个元素与第n个元素之间插入一个新元素,你就不得不把从第n个元素开始的所有后面的元素都向后移动一位来“腾位置”,这意味着对总共有N个元素的数组进行插入,平均需要移动N/2个元素(假设无限次对大小为N的数组插入一个元素到随机的位置上)。因此对数组进行插入操作是昂贵的。
但是链表的插入,则要廉价许多。向链表中两个结点间插入一个新结点(或者表尾插入一个结点)带来的问题其实就是:如何让front结点记住新结点的位置,并让新结点记住rear结点的位置?这个问题其实很好解决,只要令新结点记住rear结点的位置,然后让front结点记住新结点位置就好了。用图来简要表示一下(可以发现,即使rear是NULL也没有关系):
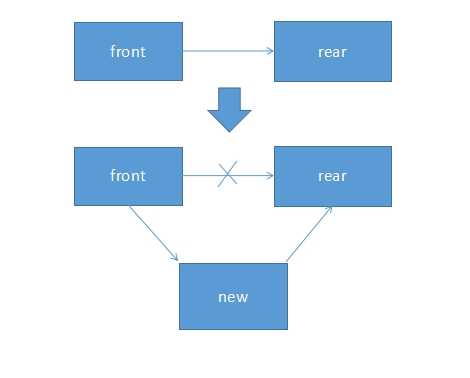
显然链表的插入代价比数组要小多了,我们不需要移动那么多的元素。其代码实现也很简单。
我们首先为新元素创建新结点,然后判断L是否为NULL(即所给链表为空,我们要插在第一个位置上),如果L不为NULL则判断插入位置N是否为负(我们允许为负数,这样就表示使用者希望插在末尾),如果L不为NULL且N不为负则将新元素插在第N位置上(如果N大于链表的总大小则会出错,因为我们的代码依然是不健壮的,但先放下这一点):
1 //注意我们接收List *而不是List,因为我们可能需要更改L所指对象 2 bool Insert(List *pL, int Elem, int N) 3 { 4 //首先为新元素开辟空间形成新结点 5 Node pElem = (Node)malloc(sizeof(struct node)); 6 pElem->data = Elem; 7 pElem->next = NULL; 8 9 //多重判断,首先看L是否为NULL,如果是则直接“接”上新结点 10 if (*pL == NULL) 11 { 12 *pL = pElem; 13 } 14 //L不为NULL,则判断使用者是否想插在链表末尾 15 else if (N < 0) 16 { 17 Node temp = *pL; 18 while (temp->next != NULL) 19 temp = temp->next; 20 temp->next = pElem; 21 22 } 23 //如果L!=NULL且N>0则插入新结点到第N位置上(注意有错!) 24 else 25 { 26 Node temp = *pL; 27 for (int i = 1;i < N-1;++i) 28 { 29 temp = temp->next; 30 } 31 pElem->next = temp->next; 32 temp->next = pElem; 33 } 34 return true; 35 }
看起来这段代码好像符合“老铁没毛病~”,然而我们前面说过了,我们并没有考虑N大于链表总结点个数+1(你可以插在链表总结点个数S+1的位置上,就相当于插在尾部)的情况。并且,除此以外(也就是即使N不越界),我们还有一个特殊情况没有考虑!!那就是N==1的情况!
假设所给链表不为空,而我们现在希望插入一个新元素作为第一个元素,那么上面的代码会出错(或者说没能实现)。
稍加分析就会发现,原因是*pL!=NULL&&N==1时我们执行的是最后一个else{}内的代码,然而temp一开始就是*pL,所以即使for循环没执行,后面的代码执行的依然是“插入到第二个位置上”。要想解决这个问题,最简单的办法就是直接再来一个else if ,也即在最后一个else{}之前再插入如下代码:
else if (N == 1) { pElem->next = *L; *L = pElem; }
这下看起来貌似圆满了,但其实我们心里都清楚,我们没有关注N越界的情况……其实,有一个办法可以方便地N越界的情况,就是令L不再直接指向第一个结点,而是指向一个非链表元素的头结点,然后头结点再指向第一个结点,头结点存放链表结点个数,这样就可以方便地知道链表有多长了。但目前我们先把这个技术放一边,只需要心中牢记我们没有考虑N越界的情况就行(因为你记得越深,后面就越容易明白为什么多加一个头结点:-P)。
对于删除操作,好吧,依然不得不提一些额外的话题。那就是链表与数组在删除操作上的不同。
我们先来看一下对于数组的删除元素我们该怎么做:删除第n个元素,就需要将第n+1个元素到最后一个元素全部向前移动一位(假设int a[N],如果a[m]被删除了,我们不将a[m+1]及后面的元素向前移动一位的话,我们该如何知道a[m]是无效的,而不是逻辑上的表的一个元素呢?)。
显然,数组中删除一个元素极其麻烦,因为你需要移动很多元素,平均情况而言,一次删除需要移动N/2个元素(假设无限次对大小为N的数组删除一个随机的位置上的元素)。这显然是个很昂贵的操作。
但是链表的删除,则要廉价许多(类似于插入操作)。删除链表中某个结点带来的问题其实就是,如何让front结点记住rear结点的位置?(不然就断链了,有点像谍战片中某个关键中间人挂了的感觉)而这个问题其实是很好解决的,就是让discard结点在挂掉之前,把它知道的rear结点的位置告诉上一个元素,然后让上一个结点“忘记”它%>_<%(当然,我们最后还要记得确切地“干掉”delete结点,不然它会存在内存中而又无法被人找到!)
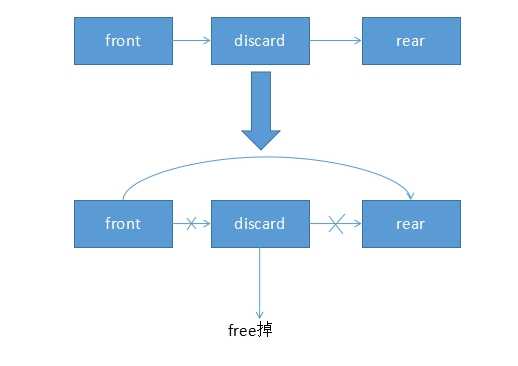
那么接下来,我们就想一想代码的过程该是怎样的。
首先,我们不再对L是否为NULL进行判断,因为L为NULL时调用delete()和delete()的参数N大于链表实际大小其实是一个性质的。接下来,类似于插入操作,我们要判断N是否小于0(我们设计原则为若N<0则表示删除最后一个结点),若N>0则判断是否N==1(这里原因类似于插入操作)
//接收List*而不是List的理由是可能需要更改L bool Delete(List *pL, int N) { //首先判断N<0,如果是则删除链表末尾结点 if (N < 0) { Node temp = *pL; while (temp->next->next != NULL) //我们在倒数第二个结点停下 { temp = temp->next; } free(temp->next); //释放最后一个结点的空间 temp->next = NULL; //然后让原倒数第二个结点的next=NULL } //对于删除第一个结点,需要特殊处理 else if (N == 1) { Node temp = *pL; *pL = (*pL)->next; free(temp); } //其他情况统一处理,暂不考虑N越界问题 else { Node temp = *pL; for (int i = 1;i < N - 1;++i) //我们在第N-1个结点处停下 temp = temp->next; //暂存第N个结点,然后令第N-1结点的next指向N+1结点,之后才可以释放第N个结点 Node discard = temp->next; temp->next = discard->next; free(discard); } return true; }
删除操作中需要特别注意的一点就是free(),因为结点的“诞生”是通过malloc来分配的空间,所以当我们决定抛弃某个结点时也一定要记得free(),否则它将占用内存空间,然而我们却没法再找到它!
上面的插入代码和删除代码都忽略了N越界的情况,这一点我们也反复说明了。接下来我们就要说一说在插入操作之后提到的那个技术,即令L指向一个非表中元素的结点。为什么我们说利用这个“头结点”我们可以解决N越界的情况呢?因为头结点若不是表中元素,那么其存储的数据就可以是自定义的,因此我们完全可以令其存储“链表的结点个数”,这样一来就解决了如何判断N是否越界的问题(和头结点中存储的size比较即可)。并且由于头结点的存在,我们不再需要接收一个类似List *这样的参数了(跟指针的指针打太多交道总是令人苦恼的╮(╯_╰)╭)。
为了实现头结点,首先我们要对结点定义等做一些修改:
//node是结点,Node是指向普通结点的 struct node { int data; struct node*next; }; typedef struct node *Node; //FirstNode特用于头结点,List也只能指向头结点 struct FirstNode { int size; struct node *next; }; typedef struct FirstNode *List;
根据新的结点,我们的三个基础操作函数也要有相应的一些更改(更加健壮,但并不完美)
//新的Find函数,我们通过success来告诉调用者是否查询成功 int Find(List L, int N, bool*success) { //若N越界或N==0则提示false if(N > L->size|| N == 0) { (*success) = false; return -1; } Node temp = L->next; for (int i = 1;i < N;++i) { temp = temp->next; } (*success) = true; return temp->data; } //新的Insert,我们不需要List*了 bool Insert(List L, int Elem, int N) { //依旧,创建新结点保存元素 Node pElem = (Node)malloc(sizeof(struct node)); pElem->data = Elem; pElem->next = NULL; if (N < 0) { //N<0且L为空链表,相当于插入到第一个结点,我们特殊对待 if (L->size == 0) { //记得增加L->size L->size++; L->next = pElem; } //N<0且L不空,则插入表尾 else { Node temp = L->next; while (temp->next != NULL) { temp = temp->next; } temp->next = pElem; L->size++; //记得增加L->size } } else if (N == 1) //若N==1则特殊对待,但即使同时L为空这么做也是对的 { //因为L->next==NULL,pElem->next=L->next实际上没做什么,与N<0且L为空时的代码一个性质 pElem->next = L->next; L->next = pElem; L->size++; //记得增加L->size } else if (N > L->size+1) //此时N越界,返回false { return false; } else //其他情况,即N>1且没有越界 { Node temp = L->next; for (int i = 1;i < N - 1;++i) //注意一下这里的循环次数 { temp = temp->next; } pElem->next = temp->next; temp->next = pElem; L->size++; //记得增加L->size } return true; } //新的delete函数,我们也不用List*了 bool Delete(List L, int N) { //如果L为空,则删除失败 if (L->size == 0) return false; if (N < 0) { //N<0且L只有一个结点,此时我们特殊对待 if (L->size == 1) { Node discard = L->next; L->next = NULL; free(discard); L->size--; } //N<0且L不止一个结点,则我们找到尾结点然后删除它 else { Node temp = L->next; while (temp->next->next != NULL) //注意循环条件,我们在倒数第二个结点停下 temp = temp->next; Node discard = temp->next; temp->next = NULL; free(discard); //记得free()以及减小L->size; L->size--; } } else if (N == 1) //若N==1则表示删除第一个结点,此时即使L->size==1也没关系,因为discard->next==NULL { Node discard = L->next; L->next = discard->next; free(discard); //记得free()以及减小L->size; L->size--; } else //N>1且没有越界,则我们找到第N个结点然后删掉它 { if (N > L->size) return false; Node temp = L->next; for (int i = 1;i < N - 1;++i) //注意循环条件,我们在N-1处停下 temp = temp->next; Node discard = temp->next; temp->next = discard->next; free(discard); //记得free()以及减小L->size; L->size--; } return true; }
有了新的带头结点的结点定义以及完整的三个基础操作函数,我们已经可以开始在main函数中对链表做一些小小的实验了,比如插入、删除、查找、删除、查找、插入……但显然我们还差一样东西,就是插入之后如何看出我插入了,而删除之后又如何看出我删除了呢?显然我们需要的是一个能够输出当前链表状态的函数,这个函数很简单:逐个“拜访”链表结点,然后printf它们的数据就行了~
void printList(List L) { Node temp = L->next; while (temp != NULL) { printf("%d\t", temp->data); temp = temp->next; } printf("\n"); }
现在,我们可以开始对链表进行一些小小的实验,或者说试验(就是利用上述三个函数和printList来玩一玩链表。最后之后自己实现一遍)
int main() { List L = (List)malloc(sizeof(struct FirstNode)); L->size = 0; L->next = NULL; Insert(L, 1, 1); Insert(L, 2, -1); Insert(L, 3, 3); Insert(L, 4, -1); printList(L); Delete(L, -1); printList(L); Delete(L, 1); printList(L); bool success = true; int answer = Find(L, 3, &success); if (success) { printf("%d\n", answer); } else { printf("Wrong!\n"); } answer = Find(L, 1, &success); if (success) { printf("%d\n", answer); } else { printf("Wrong!\n"); } return 0; }
估计有不少读者会问,很多时候我们并不是按“索引”来查找或者增加删除啊,我们有时候需要对“符合某个条件”的结点进行操作啊?其实这个问题很好解决,因为我们已经知道了查找、插入、删除的“核心思想”,要想实现诸如查找某个结点第一次出现的位置,或者删除所有符合某条件的结点等,都可以由“核心思想”+“对结点的判断”写出来,目前我们可以说是“对索引进行判断”,只要做适当更改,令函数对我们想要的条件进行判断即可。这部分的实现并不难,所以不给出相关示例,毕竟相关示例有不少,难以一一列举呢。有兴趣的初学者或者说想练练手的初学者可以试着自己去写一些诸如DeleteIf()这样的函数来对链表进行更深一步的理解~
下一次我们将要介绍的是一种特殊的“链表”,叫“游标数组”,既然又是链表又叫数组的,相比大家可以猜到,它其实就是用数组来实现链表的!其实我们本可以不用再学习游标数组,因为游标数组依然是需要事先开辟数组空间的,其诞生源于没有指针的语言,因为链表除了即用即开空间的好处外,还有插入和删除快速的优点。游标数组就是为了利用这两个优点而诞生的数据结构(之所以C语言有指针我却依然要提游标数组是因为很多人认为使用链表就是为了快速增删,而忘记了其空间节约的优点,并且误认为只有链表能做到快速插删)
--------------------------------------------------------------------------------------------------------------------------------------------------------------
分割线
后期编辑:写完之后发现貌似对于一般数据结构书上都会提到的循环链表和双向链表都未提及,所以特地补充一下。但其实循环链表和双向链表都很简单。
我们讲的链表俗称单链表,即每个结点只有一个next,且最后一个结点的next==NULL。
循环链表就是最后一个节点的next保存着第一个结点(不是头结点)的地址。
双向链表就是每个结点除了next指向下一个结点,还有一个front(也可以是别的名字啦,我随便取的╮(╯_╰)╭)指针指向前一个结点,这样可以方便以倒序遍历(比如找到某个符合某条件的结点,然后输出前面的结点之类的)
循环链表和双向链表都按需索取吧,都很容易理解很容易实现。
标签:blog 思考 代码 函数 初学 函数调用 遍历 开始 实现
原文地址:http://www.cnblogs.com/mm93/p/6576765.html