标签:赋值 length static 相对 style 希尔排序 长度 排序算法 二分插入
算法,我在路上,将自己了解的算法内容全部梳理一遍!
今天介绍简单点的,插入排序。
首先,什么是插入排序,这个维基百科上有。个人的理解,就是将一个数插入到一个已经排好序的数列当中某个合适的位置,使得增加了一个元素的新的数列依然是有序的。比如,当前有一个待排序的数组A,我们可以认为这个数组是由两部分组成的,一部分是有序的数列B,一部分是无序的数列C,将无序数列中的元素逐个的取出,添加到有序数列中,两个数列的长度是变化关系是:B从1逐次增加1,而C的长度是逐次减少1,直到B的长度和A一样长,C的长度为0.
从上面对插入排序的描述来看,插入排序是一个稳定的排序,也就是说原始元素排好序后,等值元素的位置次序关系不会变,之前靠前的,排好序后还是在前面。
那具体来说,插入排序,就基本的实现思路是什么呢?下面总结一下待排序数组A进行升序排序的实现步骤:
1.将A中的第1个元素划分到数列B中;
2.取A余下的元素归入C中,取C中首个元素赋值给一个临时变量temp;
3.将temp与B中的元素进行反向比较大小,若temp小于B中当前的值,则将B中的元素向右移动,继续逆向取B中的下一个元素;
4.若temp大于B中的当前值,则将temp值插入到B中当前位置的右边;
5.循环执行2-4的步骤,直到C中的元素全部移动到B中;
基于上述的实现步骤,下面,就用java代码,实现插入排序:
/** * @author "shihuc" * @date 2017年3月28日 */ package InsertionSort; import java.io.File; import java.io.FileNotFoundException; import java.util.Scanner; /** * @author "shihuc" * */ public class Solution { /** * @param args */ public static void main(String[] args) { File file = new File("./src/insertionSort/sample.txt"); Scanner sc = null; try { sc = new Scanner(file); int N = sc.nextInt(); for(int i=0; i<N; i++){ int S = sc.nextInt(); int A[] = new int[S]; for(int j=0; j<S; j++){ A[j] = sc.nextInt(); } insertionSort(A); print(A, i, "...."); } } catch (FileNotFoundException e) { e.printStackTrace(); } finally { if(sc != null){ sc.close(); } } } /** * 用来打印输出堆中的数据内容。 * * @param A 堆对应的数组 * @param idx 当前是第几组待测试的数据 * @param info 打印中输出的特殊信息 */ private static void print(int A[], int idx, String info){ System.out.println(String.format("No. %02d %s ====================== ", idx, info)); for(int i=0; i<A.length; i++){ System.out.print(A[i] + ", "); } System.out.println(); } /** * 直接插入法进行插入排序,升序 * * @param src 待排序的数组 */ private static void insertionSort(int src[]) { int temp; int j; /* * 实现步骤(5) * * for循环i从1开始取值,暗含数组下标0的元素被划出来了。对应实现步骤(1) */ for(int i=1; i<src.length; i++){ /* * 实现步骤(2) */ temp = src[i]; j = i - 1; /* * 实现步骤(3) */ while(j > 0 && src[j] > temp){ src[j+1] = src[j]; j--; } /* * 实现步骤(4) */ src[j+1] = temp; #注意,这里不是src[j] = temp; } } }
测试样例数据,即sampe.txt里面的内容:
5 7 2 6 3 4 5 10 9 10 2 3 1 4 6 19 11 17 8 16 11 12 11 12 17 18 13 19 21 90 23 35 7 88 12 22 112 31 11 79 9 9 18 21 23 222 121 234 90 211
下面附上测试运行的输出:
No. 00 .... ====================== 2, 3, 4, 5, 6, 9, 10, No. 01 .... ====================== 2, 1, 3, 4, 6, 8, 11, 16, 17, 19, No. 02 .... ====================== 12, 11, 12, 13, 17, 18, 19, 21, 23, 35, 90, No. 03 .... ====================== 88, 11, 12, 22, 31, 79, 112, No. 04 .... ====================== 9, 18, 21, 23, 90, 121, 211, 222, 234,
插入排序的动态过程如下(网上找的一个图,辅助理解算法过程):
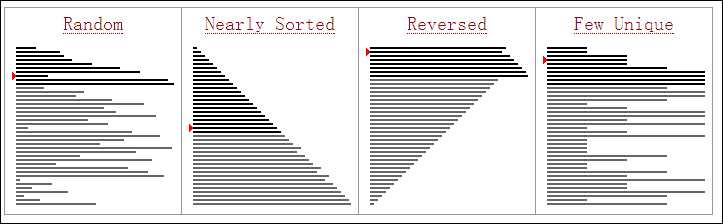
从上面的实现过程来看,存在数据移位的操作,双重循环,导致算法复杂度为O(n^2),所以,插入排序针对少量的数据排序,是可以的,性能也不是那么要紧,但是数据量比较大时,就不太合适了。
当然,上面的实现过程,是插入排序的基本实现,有其他变种的插入排序,比如折半插入排序,又叫做二分插入排序,主要是对已排好序的数列B做文章,将查找temp元素插入位置j的过程优化了下,不再对B逆序逐个比较,而是从B中的中间元素开始比较,大于中间元素的话,则再和B右边半数数据中的中间数值比较,以此类推,找到插入点。代码就不做实现了,也不难!
另外,还有一种变种的插入排序,叫希尔排序,这个相对有点特殊,单独作为一篇博文介绍吧。
标签:赋值 length static 相对 style 希尔排序 长度 排序算法 二分插入
原文地址:http://www.cnblogs.com/shihuc/p/6642445.html