关系型数据库的工作原理(四)

标签：归并排序   数据库连接   成本   style   order   ati   scan   bsp   复杂度   

查询优化：

    现代数据库都使用一种基于成本优化（参见第一部分）的方式进行优化查询，这种方式的思路是给每种基本运算设定一个成本，然后采用某种运算顺序总成本最小的方式进行查询，得到最优的结果。

    为简化理解，对数据库的查询重点放在查询时间复杂度上，而不考虑CPU消耗，内存占用与磁盘I/O，且相比与CPU消耗，数据库瓶颈也更多在磁盘I/O。

    索引

    B+树、bitmap index等都是常见的索引实现方式，不同的索引实现有不同的内存消耗、I/O以及CPU占用。一些现代数据库还可以创建临时索引。

    获取（数据）方式：

    在进行连接查询操作之前，需要先获取数据，以下是常见的获取方式（数据获取的关键在磁盘I/O，故在衡量获取方式时，考察量也应在此）。

    全扫描

    全扫描（full scan or scan），即扫描整个表或者所有索引，全表扫描的磁盘I/O明显高于全索引扫描。

    范围扫描

    AGE字段有索引，当sql使用谓词where age < 20 and age >20时(between and会在上面查询解析阶段改成<和>)，便会使用范围索引。参见第一部分知，范围扫描的复杂度为log(N)+M，N是索引中的数据量，M是搜索范围内行数，可见范围扫描比全索引扫描有更低的磁盘I/O。

    唯一扫描

    如果想只需要从索引中取一个值，可用唯一扫描(unique scan)。

    根据rowid获取

    当要查询索引行相关的列时，便会用到rowid，比如查询age=28(age上有索引，name无索引)的人的名字:

Select name from person where age = 28;

    以上的查询会按照：查询索引列age，过滤出age=28的所有行，然后按照查询出来的行号查name列，即先读索引再读表。但下面列子就不用读表了（name有索引）:

Select location.street from person, localtion where person.name = person.name;

    该方式在数据量不大时是比较有效的，但当数据量很大时，相当于全扫描了。

    其他获取方式

　　　以oracle为例。

    连接

    获取到数据后对数据进行连接运算，这里介绍三种连接方式:merge join, hash join,     nested loop join，以及引入inner relation和outer relation两个概念。关系数据库中定义了“关系”的定义，它可以是：一个表，一个索引以及前面运算的结果。

    连接两个关系时，数据库连接运算处理两个关系方式可能不同，本文定义:

    连接运算符左边的关系称为outer relation；

    连接运算符右边的关系称为inner relation。

    比如a join b，a称为outer relation（常看见的是外表说法），b称为inner relation（常看见的是内表说法）。多数情况下 a join b 与b join a的成本是不一样的。该部分假定outer relation有N个元素，inner relation有M个元素（实际情况下，这些信息数据库通过统计可以知道，如上部分）。

　嵌套循环连接（Nested loop join）:

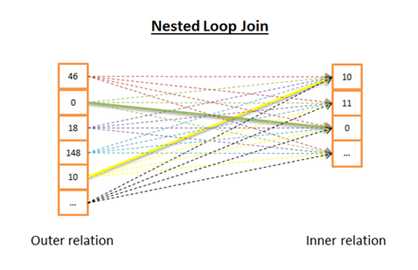
　　　　　　　　　              　Fig. 11

　　一般分为两个步骤：

1. 读取outer relation 每一行
2. 检查inner relation中的每一行是否匹配连接

　　伪代码：  

nested_loop_join(array outer, array inner)
  for each row a in outer
    for each row b in inner
      if (match_join_condition(a,b))
        write_result_in_output(a,b)
      end if
    end for
  end for

　　显然时间复杂度为(N*M)。从磁盘I/O考虑，算法需要从磁盘读N+N*M行。可知，当M足够小时，只需要读N+M次，这样就可以把读取结果放到内存中，所以一般情况下都会将小的relation作为inner relation。

　　当然这虽然改善了磁盘I/O，时间复杂度并没有变化。如果进一步优化磁盘I/O，还可以考虑将inner relation用索引来替换。　

　　考虑尽可能将inner relation放到内存，做一个改进，基本思路：

1. 不逐行读取两个关系，而是分组读取，将组信息放到内存中；
2. 对比（内存中）的组间行，保留符合连接条件的行
3. 依次加载其他组直至对比两关系中所有组。

     伪代码

// improved version to reduce the disk I/O.
nested_loop_join_v2(file outer, file inner)
  for each bunch ba in outer
  // ba is now in memory
    for each bunch bb in inner
        // bb is now in memory
        for each row a in ba
          for each row b in bb
            if (match_join_condition(a,b))
              write_result_in_output(a,b)
            end if
          end for
       end for
    end for
   end for

　　该版本相比之前版本时间复杂度没有变化，但磁盘I/O明显变小了：number_of_bunches_for(outer)+ number_of_bunches_for(outer) * number_of_ bunches_for(inner)，而且可知增加分组的大小，即每次读取更多数据，还能继续减小读取次数。　

    哈希连接（hash join）

　　哈希连接更加复杂，但大多场合中比循环嵌套连接成本更低。

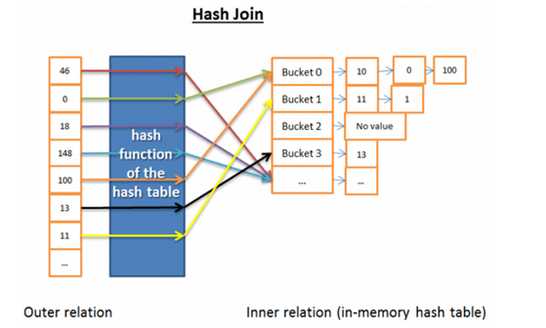
　　　　　　　　　　　　　　　　　　Fig. 12

　　基本思路：

1. 获取inner relation中的所有元素
2. （根据inner relation中的元素）构建一个常住内存hash table
3. 逐个获取outer relation所有元素
4. 计算每个元素的哈希值(利用哈希函数计算哈希表)，与inner relation中的元素逐个比较，以确定inner relation对应哪个bucket
5. 确定bucket与outer relation对应关系（buckt是否存在outer relation中元素）

　　分析其时间复杂度：inner relation分为x个buckets，outer relation与buckets对比的次数取决于buckets中的元素个数。哈希函数对各个关系中的元素是均匀分布的，也就是说buckets的大小是相同的。

　　时间复杂度：(M/X) * N + cost_to_create_hash_table(M) + cost_of_hash_function*N，当hash函数创建足够小的buckets时，比如buckets只有一个元素，那么时间复杂度可以为(M+N)。

　　内存占用更小磁盘I/O更小版本：

1. 对inner 和 outer relation都创建一个hash table
2. 把创建的hash tables放入磁盘
3. compare the 2 relations bucket by bucket (with one loaded in-memory and the other read row by row)

  Merge join　

　　Merge join是唯一产生排序结果的连接查询。

　　排序

　　在最开始介绍过归并排序，可以看到归并排序是一个很好的算法（当然如果不考虑内存情况下会有更好的算法，比如hash join）。但在以下条件时，一般会选择merge join。

1. 某个关系（表中）已经排好序
2. 某个关系连接条件建有索引
3. 连接条件产生的是中间结果，而该中间结果已经排序.

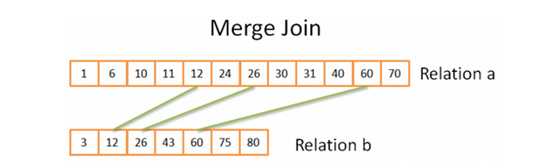
　　　　　　　　　　　　　　　　　　　　　　Fig. 13

　　Merge的过程和前面介绍的merge sort很相似，但是不会逐个读取两个关系元素，只会选择符合连接条件的元素。基本思路如下：

1. 对比两个relations的当前元素；
2. 如果两个元素相等，取出该元素，对比下面的元素；
3. 如果两个元素不相等，将较小元素进入下一次对比。
4. 重复以上，直到两个relations都处理到最后一个元素。

　　以上思路是在俩relations已经排好序且任一关系中不存在相同元素的简化模型下，具体的要复杂的多。

　　时间复杂度，如果两个relations已经排序好，复杂度为N+M；如果需先排序再连接，复杂度为(N*log(N)+M*log(M))。

　　伪代码

mergeJoin(relation a, relation b)
  relation output
  integer a_key:=0;
  integer  b_key:=0;
 
  while (a[a_key]!=null and b[b_key]!=null)
     if (a[a_key] < b[b_key])
      a_key++;
     else if (a[a_key] > b[b_key])
      b_key++;
     else //Join predicate satisfied
      write_result_in_output(a[a_key],b[b_key])
      //We need to be careful when we increase the pointers
      if (a[a_key+1] != b[b_key])
        b_key++;
      end if
      if (b[b_key+1] != a[a_key])
        a_key++;
      end if
      if (b[b_key+1] == a[a_key] && b[b_key] == a[a_key+1])
        b_key++;
        a_key++;
      end if
    end if
  end while

算法比较选择：

1. 内存的占用：如果没有足够的内存，基本要告别强大的 hash join （ 至少也告别全内存 hash join）。
2. 2个关系的数据量：比如要连接的两个表，一个数据量特别巨大，一个又很小很小，这时候 nested loop join 的效果要比 hash join 好，因为 hash join 给那个数据量巨大的表创建 hash 表就很费事。 如果两个表都有巨量的数据， nested loop join 连接方式的 CPU 负载会比较大；
3. 索引的方式： 如果连接的两个关系都有 B+树索引，那肯定是 merge join 效果最好；
4. 结果是否需要排序： 如果希望这次连接得到一个排序的结果（这样就可以使用 merge join 方式实现下一个连接），或者查询本身（有 ORDER BY/GROUP BY/DISTINCT 运算符）要求的排序的结果；如果是这个情况，即使当前要连接的 2 个关系本身并没有排好序， 依然建议选择稍微有点费事的 merge join（可以给出排序的结果）；
5. 连接的 2 个关系本身已经排序： 这个情况，必须用 merge join；
6. 连接类型： 如果是等值连接（比如： tableA.col1 = tableB.col2）？或者是内连接、外连接、笛卡尔积、自连接？有些连接方式可能不能处理这些不同类型的连接；
7. 数据的分布： 如果连接条件的数据扭曲了（比如要连接表 PERSON 连接条件是列“姓”，但是意味的是很多人的姓是相同的），这个情况如果使用 hash join 一定会带来灾难，对吧？因为哈希函数计算后各个 buckets 上数据的分布肯定存在巨大的问题 （有些 bucket 很小，只有一两个元素；而有些 buckets 太大，好几千的元素） 。

 下一篇将有一个简单的例子简要说明改过程。

关系型数据库的工作原理(四)

标签：归并排序   数据库连接   成本   style   order   ati   scan   bsp   复杂度   

原文地址：http://www.cnblogs.com/space-place/p/6655771.html