标签:定义 最优 blog com 例子 保留 log title images
作者:桂。
时间:2017-04-01 06:39:15
链接:http://www.cnblogs.com/xingshansi/p/6654372.html
声明:欢迎被转载,不过记得注明出处哦~

【学习笔记07】
未完待续
前言
西蒙.赫金的《自适应滤波器原理》第四版第四章:最速下降算法。优化求解按照有/无约束分类:如投影梯度下降算法((Gradient projection)便是有约束的优化求解;按照一阶二阶分类:梯度下降(Gradient descent)、Newton法等;按照偏导存在与否分类:如梯度下降、次梯度下降(Subgradient descent)等.本文主要整理:梯度下降法在维纳滤波中的应用.
一、原理思想
对于准则函数:
![]()
需要寻找最优解$w_o$,使它对所有$w$满足$J(w_o) \le J(w)$。可以利用迭代下降的思路求解:
从初始值$w(0)$出发, 产生一系列权向量$w(1)$,$w(2)$...,使得准则函数每一次迭代都是下降的:$J(w(n+1)) < J(w(n))$,其中$w(n)$是权向量的过去值,$w(n+1)$是更新值。
定义梯度:
$g = \nabla J\left( w \right) = \frac{{\partial J\left( w \right)}}{{\partial w}}$
负梯度方向为减小方向:
$w(n + 1) = w(n) - \mu \cdot g(n)$
为了说明准则函数随着迭代下降,从一阶泰勒展开可以观察:
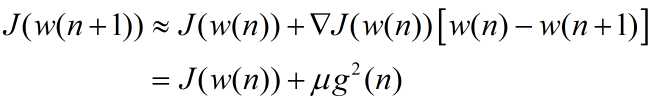
二、应用实例
仍然借助维纳滤波一文的例子:
已知:
含有噪声的正弦波:$y(n) = x(n) + w(n) = \sin (2\pi fn + \theta ) + w(n)$.
其中$f = 0.2$为归一化频率[-1/2, 1/2],$\theta$为正弦波相位,服从[0,2$\pi$]的均匀分布,$w(n)$为具有零均值和方差$\sigma^2 = 2$的高斯白噪声。
求:
时域维纳滤波器。假设滤波器为时域滤波器时$M=2$.
首先求解相关矩阵:
$x(n)$为广义平稳随机过程,可以计算其自相关函数:
${r_{xx}}\left( m \right) = \cos (2\pi fn)$
得到关于均方误差的准则函数:
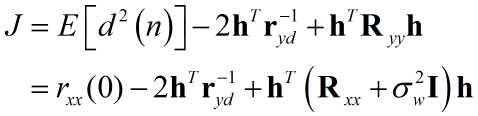
代入数值:
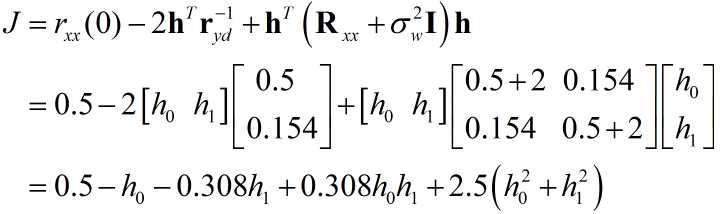
迭代的时候,可以保留矩阵的形式,也可以利用代数的形式,形式不同但本质相同,以矩阵为例:
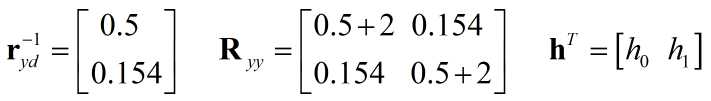
得到梯度$\nabla J = - 2{\bf{r}}_{yd}^{ - 1} + 2\;{{\bf{R}}_{yy}}{\bf{h}}$.
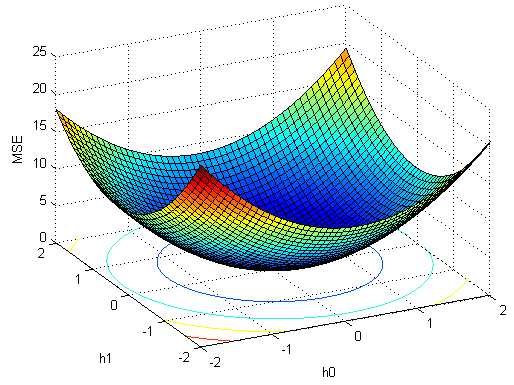
对应搜索代码:
r_yd = [0.5 0.154]‘;
R_yy = [2.5 0.154;0.154 2.5];
h_est = [0 0]‘;
deltaJold = Inf;
mu = 0.001;
for i = 1:2000
deltaJ = -2*r_yd+2*R_yy*h_est;
if abs(deltaJ-deltaJold)<1e-5
break;
end
h_est = h_est - mu*deltaJ
deltaJold = deltaJ;
end
即可得出最优解$h = [0.197 , 0.0495]‘$。
三、稳定性
上文中$\mu$取0.001,$\mu$如何取值才能保证梯度正常下降呢?事实上,如果$\mu$过大结果会往外发散而不是收敛于最优点。
借助维纳滤波一文可以知道,
${w_o} = \;{\bf{R}}_{_{yy}}^{ - 1}{\bf{r}}_{yd}^ - $
从而有:
![]() 记$c(n) = w_o - w(n)$:
记$c(n) = w_o - w(n)$:
$c(n + 1) = c(n)\left( {{\bf{I}} - 2\mu {{\bf{R}}_{yy}}} \right)$
对于正定矩阵,存在正交矩阵:
${{\bf{R}}_{yy}} = {\bf{Q\Lambda }}{{\bf{Q}}^{ - 1}}$
即${\bf{I}} - 2\mu {{\bf{R}}_{yy}}{\rm{ = }}{\bf{Q}}\left( {{\bf{I}} - 2\mu {\bf{\Lambda }}} \right){{\bf{Q}}^{ - 1}}$,为此保证最大特征值小于1即可保证收敛:
![]()
如对应上面$h$的求解,$\frac{1}{{{\lambda _{\max }}}}= 0.3768$,用上面的程序容易验证$\mu = 0.37$时满足条件,可以收敛;$\mu = 0.38$则发散,无法得到最优值。
四、理论扩展
A-批量梯度下降
引入误差,均方系数估计。
B-随机梯度下降
C-Newton-Raphson法
参考:
标签:定义 最优 blog com 例子 保留 log title images
原文地址:http://www.cnblogs.com/xingshansi/p/6654372.html