标签:固定 数学建模 代码段 规则 好的 好处 通过 语句 不同的
函数是组织好的,可重复使用的,用来实现单一,或相关联功能的代码段。
补充:
1.编程语言中的函数与数学意义的函数是截然不同的俩个概念,编程语言中的函数是通过一个函数名封装好一串用来完成某一特定功能的逻辑,数学定义的函数就是一个等式,
等式在传入因变量值x不同会得到一个结果y,这一点与编程语言中类似(也是传入一个参数,得到一个返回值),不同的是数学意义的函数,传入值相同,得到的结果必然相同且没
有任何变量的修改(不修改状态),而编程语言中的函数传入的参数相同返回值可不一定相同且可以修改其他的全局变量值(因为一个函数a的执行可能依赖于另外一个函数b的结果,
b可能得到不同结果,那即便是你给a传入相同的参数,那么a得到的结果也肯定不同)。
2.函数式编程就是:先定义一个数学函数(数学建模),然后按照这个数学模型用编程语言去实现它。至于具体如何实现和这么做的好处,且看后续的函数式编程。
函数能提高应用的模块性,和代码的重复利用率。
你已经知道Python提供了许多内建函数,比如print()。但你也可以自己创建函数,这被叫做用户自定义函数。
你可以定义一个由自己想要功能的函数,以下是简单的规则:
Python 定义函数使用 def 关键字,一般格式如下:
def 函数名(参数列表):
函数体
默认情况下,参数值和参数名称是按函数声明中定义的的顺序匹配起来的。
1.形参变量只有在被调用时才分配内存单元,在调用结束时,即刻释放所分配的内存单元。因此,形参只在函数内部有效。函数调用结束返回主调用函数后则不能再使用该形参
变量(本质就是变量名)
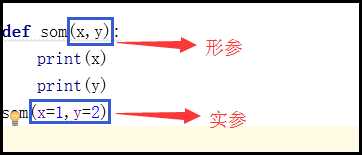
2.实参可以是常量、变量、表达式、函数等,无论实参是何种类型的量,在进行函数调用时,它们都必须有确定的值,以便把这些值传送给形参。因此应预先用赋值,输入等办
法使参数获得确定值(实参必须要有一个明确的值,可被当成变量值)
3.位置参数和关键字(标准调用:实参与形参位置一一对应;关键字调用:位置无需固定)
4.默认参数(默认参数必须注意的问题是:默认参数必须放到位置参数的后面)
5.参数组
重点在*,后面的args相当于一个变量名,可以自己定义的。它的本质就是将标准调用剩下的值集中转变为元组。
#*args的运用
def foo(x,*args): #args=(2, 3, 4, 5, 6, 6, ‘a‘, ‘b‘)将多的对应值转为元组
print(x)
print(args)
foo(1,2,3,4,5,6,6,‘a‘,‘b‘) #调用函数
1 #x的值
(2, 3, 4, 5, 6, 6, ‘a‘, ‘b‘) #args的值一个元组
#从形参的角度
def foo(*args): #foo(x,y,z)参数个数可以至多个
print(args)
foo(1,2,3) #没有个数限制
(1, 2, 3) #输出结果
#*args=*(1,2,3)
---------------分割线-----------------
#从实参的角度
def bar(x,y,z):
print(x)
print(y)
print(z)
bar(*(1,2,3,4)) #bar(1,2,3,4)这个会报错,只需3个值,但有4个值,不能一一对应。
bar(*(1,2,3)) #这个就匹配了
1 #以下就是输出的结果
2
3
#*args与位置参数和默认参数混用:*args要放到位置参数后面,默认参数要放最后。
def foo(x,*args,y=1):
print(x)
print(y)
print(args)
foo(1,2,3,4,5,6,7,8,9,10,y=10000) #调用函数
1 #x的值
10000 #y的值
(2, 3, 4, 5, 6, 7, 8, 9, 10) #args的值元组
重点在**,后面的kwargs相当于一个变量名,可以自己定义的。它的本质就是将关键字调用剩下的值集中转变为字典。
#**kwargs的运用:
def foo(x,**kwargs): #kwargs = {‘y‘: 1, ‘z‘: 2}
print(x)
print(kwargs)
foo(1,y=1,z=2) #调用函数
1 #x的值
{‘y‘: 1, ‘z‘: 2} #kwargs的值,转为了一个字典
#从形参的角度(形参的个数是由调用函数参数的实参个数决定的)
def foo(**kwargs): #foo(x=1,y=2,z=3)参数个数可以至多个
print(kwargs)
foo(x=1,y=2,z=3) #调用函数,没有个数限制
#**kwargs = **{"x":1,"y":2,"z":3}
--------------------分隔线--------------------
#从实参的角度(实参的个数是由形参的个数决定的)
def foo(x,y,z):
print(x)
print(y)
print(z)
foo(**{‘x‘: 1, ‘y‘: 2, ‘z‘: 3,"a":4}) #报错,只需3个值,但有4个值,不能一一对应。
foo(**{‘x‘: 1, ‘y‘: 2, ‘z‘: 3}) #这个匹配了 foo(x=1,y=2,z=3)
1 #以下为输出结果
2
3
def foo(x,a=4,**kwargs): #混合使用参数
print(x)
print(a)
print(kwargs)
foo(1,y=2,z=3) #使用默认参数
1 #输出结果
4
{‘y‘: 2, ‘z‘: 3}
foo(1,5,y=2,z=3) #修改默认参数
1
5
{‘y‘: 2, ‘z‘: 3}
从形参角度:
def foo(x,*args,a=4,**kwargs): #使用默认参数时,注意默认参数的位置要在args之后kwargs之前
print(x)
print(a)
print(args)
print(kwargs)
foo(1,5,6,7,8,y=2,z=3) #调用函数,不改默认参数
1 #x的值
4 #a的值
(5, 6, 7, 8) #args的值
{‘y‘: 2, ‘z‘: 3} #kwargs的值
------------------分隔线-----------------------
def foo(x,a=4,*args,**kwargs): #注意:当需要修改默认参数时,要调整默认参数的位置,要放在args之前即可,但不可放在开头。
print(x)
print(a)
print(args)
print(kwargs)
foo(1,9,5,6,7,8,y=2,z=3) #调用函数,修改默认参数a为9
1 #x的值
9 #被修改后a的值
(5, 6, 7, 8) #args的值
{‘y‘: 2, ‘z‘: 3} #kwargs的值
从实参角度:
def foo(x,*args,a=4,**kwargs): #使用默认参数时,注意默认参数的位置要在args之后kwargs之前
print(x)
print(a)
print(args)
print(kwargs)
foo(1,*(5,6,7,8),**{"y":2,"z":3}) #调用函数,不改默认参数
1 #x的值
4 #默认a的值
(5, 6, 7, 8) #args的值
{‘y‘: 2, ‘z‘: 3} #kwargs的值
-----------------分隔线-------------------
def foo(x,a=4,*args,**kwargs): #注意:当需要修改默认参数时,要调整默认参数的位置,要放在args之前,但不可放在开头
print(x)
print(a)
print(args)
print(kwargs)
foo(1,9,10,*(5,6,7,8),**{"y":2,"z":3}) #调用函数,修改默认参数a为9
1 #x的值
9 #修改默认参数a后的值
(10, 5, 6, 7, 8) #args的值
{‘y‘: 2, ‘z‘: 3} #kwargs的值
局部变量:在子程序中定义的变量称为局部变量;
全局变量:在程序的一开始定义的变量称为全局变量。
全局变量作用域是整个程序,局部变量作用域是定义该变量的子程序。
注意当全局变量与局部变量同名时:
在定义局部变量的子程序内,局部变量起作用;在其它地方全局变量起作用。
标签:固定 数学建模 代码段 规则 好的 好处 通过 语句 不同的
原文地址:http://www.cnblogs.com/Michael--chen/p/6674921.html