问题描述
题目很简单,给出N个数字,不改变它们的相对位置,在中间加入K个乘号和N-K-1个加号,(括号随便加)使最终结果尽量大。因为乘号和加号一共就是N-1个了,所以恰好每两个相邻数字之间都有一个符号。例如:
N=5,K=2,5个数字分别为1、2、3、4、5,可以加成:
1*2*(3+4+5)=24
1*(2+3)*(4+5)=45
(1*2+3)*(4+5)=45
……
输入格式
输入文件共有二行,第一行为两个有空格隔开的整数,表示N和K,其中(2<=N<=15, 0<=K<=N-1)。第二行为 N个用空格隔开的数字(每个数字在0到9之间)。
输出格式
输出文件仅一行包含一个整数,表示要求的最大的结果
样例输入
5 2
1 2 3 4 5
样例输出
120
样例说明
(1+2+3)*4*5=120
题目解析:
本题涉及到一种算法——动态规划。
(1)动态规划思想
在分治求解过程中,有些子问题被重复计算了许多次。如果能够保存已解决的子问题的答案,而在需要时再找出,就可以避免大量重复问题的计算,从而得到多项式时间算法。
(2)设计动态规划的步骤
① 找出最优解的性质,并刻画其结构特征;
② 递归地定义最优值(写出动态规划方程);
③ 以自底向上的方式计算出最优值(填入表格);
④ 根据计算最优值时得到的信息,构造一个最优解。
说明: a.步骤 ① ~ ③ 是动态规划算法的基本步骤;
b.在只需要求出最优值的情况,步骤 ④ 可以省略;若需要求出一个最优解,则必须要有第 ④ 步。
(3)动态规划的特征
① 最优子结构
当问题的最优解包含了其子问题的最优解,称该问题具有最优子结构性质。
② 重叠子问题
在用递归算法自顶向下解问题时,每次产生的子问题并不总是新问题,有些子问题被反复计算多次。动态规划算法正是利用了这种子问题的重要性质,对每一个子问题只求 解一次,而后将其解保存在一个表格中,在以后尽可能多地利用这些子问题。
以题目给出的样例输入为例,分析动态规划算法:
(1)利用 sum 数组将前 i 个数之和保存。
(2)利用 dp 数组来保存前 i 个数有 0 个乘号时的最大值(全加时的值,与 sum 数组相同),即 dp[i][0];
(3)在动态规划算法中,从第二( i 从 2 开始)个数后开始加乘号,前 i 个数循环累加 i - 1 (j 从 1 开始,到 i -1 结束,且不能大于 k)个乘号,乘号位置循环从第一个数后的位置到第 i 个数前的位置(p 从 2 开始, 到 i 结束);
step 1: i = 2 j = 1 p = 2 说明:前两个数,有一个乘号,位置在第二个数前面
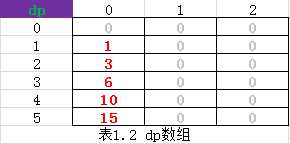
dp[2][1] = 0 说明:前两个数一个乘号时,值为 0 (表1.2中 dp[2][1])
dp[1][0] x ( sum[2] - sum[1] ) = 2 说明:前一个数没有乘号乘上前两个数之和减去前一个数之和,即前一个数乘第二个数(1*2 = 2)
dp[2][1] = max( 0 , 2 ) 说明:填入 dp 表中
step 2: i = 3 j = 1 p = 2 说明:前三个数,有一个乘号,位置在第二个数前面
dp[3][1] = 0 说明:前三个数一个乘号时,值为 0 (表1.2中 dp[3][1])
dp[1][0] x ( sum[3] - sum[1] ) = 2 说明:前一个数没有乘号乘上前三个数之和减去前一个数之和,即前一个数乘前两个数之和(1*(2+3) = 5)
dp[3][1] = max( 0 , 5 ) 说明:填入 dp 表中
step 3: i = 3 j = 1 p = 3 说明:前三个数,有一个乘号,位置在第三个数前面
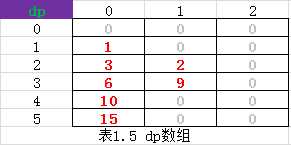
dp[3][1] = 5 说明:前三个数一个乘号时,值为 0 (表1.2中 dp[3][1])
dp[2][0] x ( sum[3] - sum[2] ) = 9 说明:前两个数没有乘号乘上前三个数之和减去前两个数之和,即前一个数乘第三个数之和((1+2)* 3) = 9)
dp[3][1] = max( 5 , 9 ) 说明:填入 dp 表中
. . . . . .
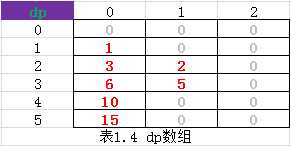
只到所有的循环执行结束,一共 19 步。dp 表最终结果为:
当 5 个数有 2 个乘号时,最大值应为 dp[5][2] = 120。在循环执行过程中,我们不用担心 dp[p-1][j-1] * (sum[i] - sum[p-1]) 究竟是那几个数得到的结果,而使用它的值就可以啦,这就是动态规划最重要的特性之一!
示例代码:
1 import java.io.BufferedReader;
2 import java.io.IOException;
3 import java.io.InputStreamReader;
4
5 public class Main {
6 public static void main(String[] args) throws IOException {
7 BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
8 String[] str = br.readLine().split(" ");
9 int n = Integer.parseInt(str[0]);
10 int k = Integer.parseInt(str[1]);
11
12 long[][] dp = new long[n+1][k+1]; //dp[i][j]表示前i个数中有j个乘号时,所得最大值
13 int[] sum = new int[n+1]; //前i个数之和
14
15 str = br.readLine().split(" ");
16 for(int i = 1; i <= n; i++) {
17 sum[i] = sum[i-1] + Integer.parseInt(str[i-1]);
18 }
19
20 //没有乘号的情况,即连加的情况
21 for(int i = 1; i <= n; i++) {
22 dp[i][0] = sum[i];
23 }
24 //动态规划
25 for(int i = 2; i <= n; i++) { //前i个数
26 for(int j = 1; j <= i-1 && j <= k; j++) { //乘号的个数
27 for(int p = 2; p <= i; p++) { //乘号的位置
28 dp[i][j] = max(dp[i][j], dp[p-1][j-1] * (sum[i] - sum[p-1]));//求前i个数有j个乘号时的最大值
29 }
30 }
31 }
32
33 System.out.println(dp[n][k]);
34 }
35
36 /**
37 * 求最大数
38 * @param a 参数1
39 * @param b 参数2
40 * @return a b中的最大数
41 */
42 private static long max(long a, long b) {
43 return a>b?a:b;
44 }
45 }