标签:处理 play display 复习 images 排列 idt 最小 输出
(注:本文的相关叙述和图片摘自《数据结构与算法分析新视角》(周幸妮等),因此本文只是我的一个复习记录,详细的论述请参考该书。)
对于一个完全二叉树来说,如果所有的结点(叶子结点除外)的值都大于(小于)其左右孩子结点的值,那么这个完全二叉树就被成为一个大(小)根堆。如下图所示。按照堆的定义可以发现,堆顶结点(二叉树的根结点)一定对应整个序列中的最大(小)记录。这样一来,可以设计一种排序思路,每次将堆的堆顶记录输出,同时调整剩余的记录,使它们从新排成一个堆。重复这个过程,就能最终得到一个有序的序列,完成排序的过程,这种方法称之为堆排序。
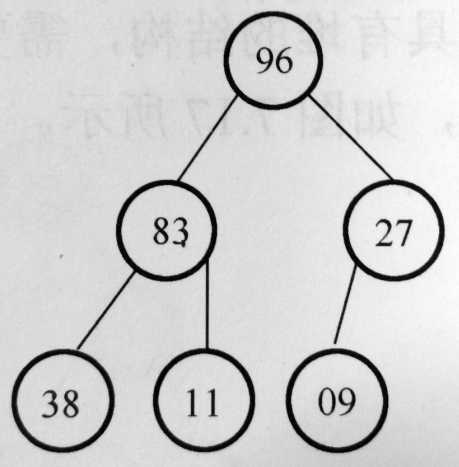
因此,对于堆排序来说,主要有两个问题:
以序列{49,38,65,97,76,13,27,49,55,04}为例,介绍生成最小堆的思路。我们知道一棵完全二叉树的最后一个非叶子结点的索引为[n/2],因此在本例中,选择第5个记录{76}作为初始筛选点。首先比较{76}与其左右孩子结点记录的大小,并按照筛选的结果进行交换,因此得到下图2的结果。接下来对倒数第二个非叶子结点进行处理,结果如下图3所示。重复这个步骤,可以得到一个结构完整的最小堆,如下图4所示。
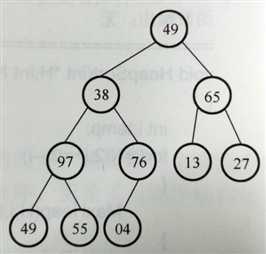
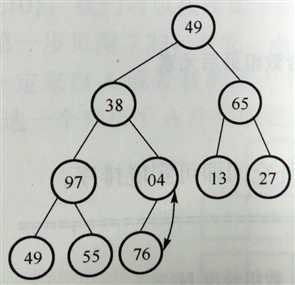
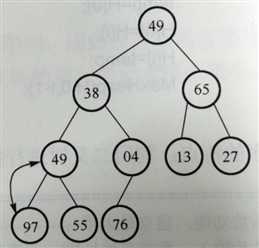
(1)序列直接构成完全二叉树 (2)一次筛选之后的完全二叉树 (3)二次筛选之后的完全二叉树
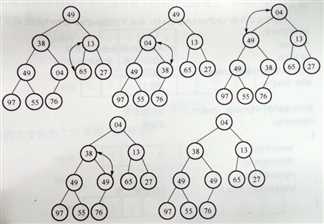
(4)经过多次筛选之后的最小堆
以序列{13,38,27,49,76,65,49,97}为例,介绍堆排序的思路。
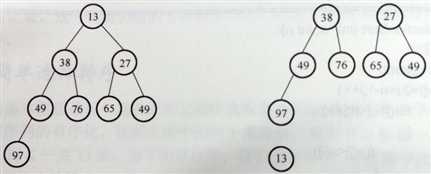
初始堆 输出堆顶元素后的情形
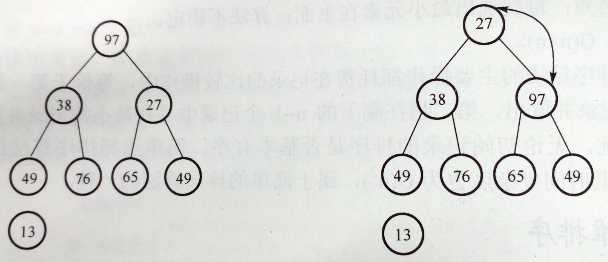
最后一个记录暂放于堆顶 一次调整之后的情形
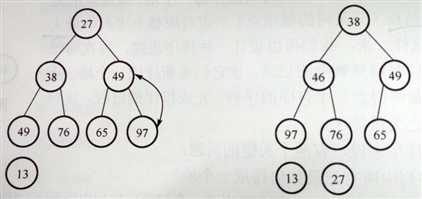
二次调整之后的情况 输出记录{27}之后再排成一个堆
重复上述步骤,最终就可以生成一个有序序列。
标签:处理 play display 复习 images 排列 idt 最小 输出
原文地址:http://www.cnblogs.com/jmliao/p/6706762.html