标签:wrap neu 关系数据库 部分 .com 第二范式 情况 rdbms pac
简单的说,
第一范式就是原子性,字段不可再分割;
第二范式就是完全依赖,没有部分依赖;
第三范式就是没有传递依赖。
1NF的定义为:符合1NF的关系中的每个属性都不可再分。下表所示的情况,就不符合1NF的要求。
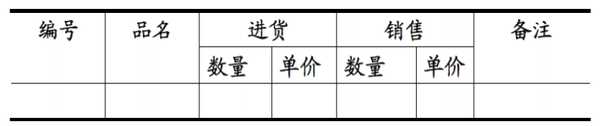
1NF是所有关系型数据库的最基本要求,也就是说,只要在RDBMS中已经存在的数据表,一定是符合1NF的。如下表所示:

2NF的定义为:在1NF的基础之上,消除了非主属性对于码的部分函数依赖。 例如: 对于下仅仅符合1NF的下表
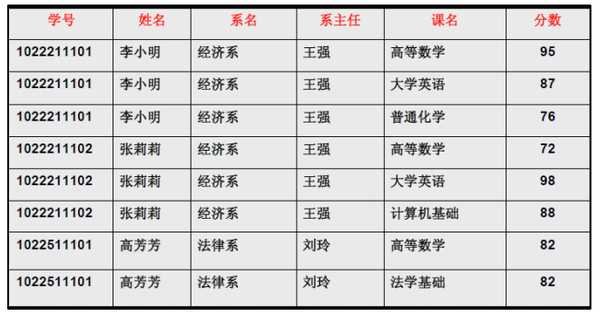
仍会存在一些问题:
数据冗余过大: 学号、姓名、系名、系主任这些数据重复多次。每个系与对应的系主任的数据也重复多次
插入异常: 假如学校3月份新建了一个系,等到8月份才招生,那么无法将系名与系主任的数据单独地添加到数据表中去
删除异常: 假如将某个系中所有学生相关的记录都删除,那么所有系与系主任的数据也就随之消失了
修改异常: 假如李小明转系到法律系,那么为了保证数据库中数据的一致性,需要修改三条记录中系与系主任的数据
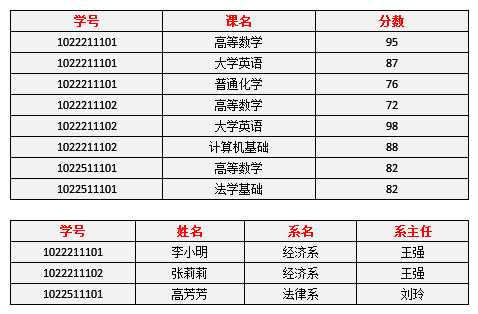
3NF的定义为:在2NF的基础之上,消除了非主属性对于码的传递函数依赖。
仅仅符合2NF的要求,很多情况下还是不够的,原因在于仍然存在非主属性(系主任)对于码(学号)的传递函数依赖。改进后如下:
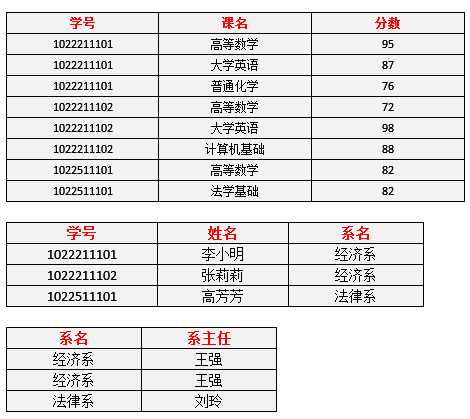
改进:
删除某个系中所有的学生记录,该系的信息不会丢失。
插入一个尚无学生的新系的信息。因为系表与学生表目前是独立的两张表,所以不影响。
数据冗余更加少了。
总结上边 1NF -> 2NF -> 3NF 如下图:
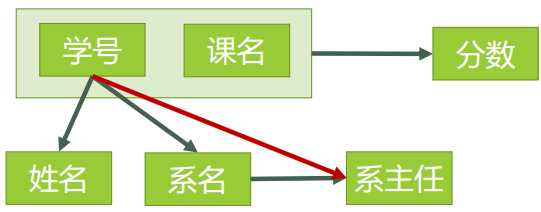
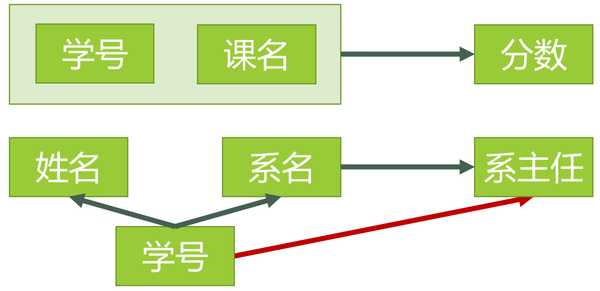
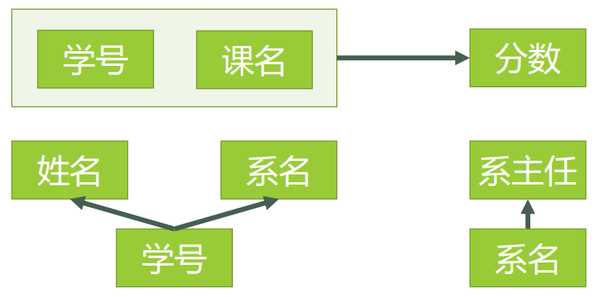
1. 函数依赖: 若在一张表中,在属性(或属性组)X的值确定的情况下,必定能确定属性Y的值,那么就可以说Y函数依赖于X,写作 X → Y。
例如: 系名 → 系主任, (学号,课名) → 分数
2. 完全函数依赖: 在一张表中,若 X → Y,且对于 X 的任何一个真子集(假如属性组 X 包含超过一个属性的话),X ‘ → Y 不成立,那么我们称 Y 对于 X 完全函数依赖,记作:![]()
例如: 学号 F→ 姓名, (学号,课名) F→ 分数 (F在箭头上边。。。)
3.部分函数依赖: 假如 Y 函数依赖于 X,但同时 Y 并不完全函数依赖于 X,那么我们就称 Y 部分函数依赖于 X,
记作 ![]()
例如: (学号,课名) P→ 姓名 (P在箭头上边。。。)
4.传递函数依赖:假如 Z 函数依赖于 Y,且 Y 函数依赖于 X (严格来说还有一个X 不包含于Y,且 Y 不函数依赖于Z的前提条件),那么我们就称 Z 传递函数依赖于 X ,
记作![]()
5. 码: 设 K 为某表中的一个属性或属性组,若除 K 之外的所有属性都完全函数依赖于 K,那么我们称 K 为候选码,简称为码。
一张表中可以有超过一个码。通常选择其中的一个码作为主码。
例如:(学号、课名)这个属性组就是码。 我们可以理解为:假如当 K 确定的情况下,该表除 K 之外的所有属性的值也就随之确定,那么 K 就是码。
ref:
https://www.zhihu.com/question/24696366/answer/29189700
http://aijuans.iteye.com/blog/1629645
标签:wrap neu 关系数据库 部分 .com 第二范式 情况 rdbms pac
原文地址:http://www.cnblogs.com/pinganzi/p/6710435.html