标签:class oid ++ sts 提升 时间 sel 步骤 src
假设我们有如下一个数组:
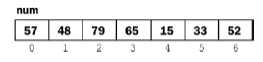
使用选择排序算法对这个数组进行排序,步骤如下:
第 1 次
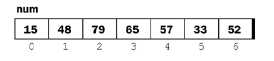
第 2 次
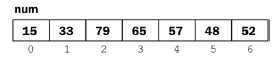
第 3 次
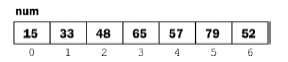
按照上面的方式进行到第6次,就完成了排序,用 Java 实现的选择排序算法代码如下:
public class SelectionSort { public static void main(String[] args){ int[] arr = new int[]{3,4,1,5,7,6,0,2}; sort(arr); printArr(arr); } public static void sort(int[] arr){ int length = arr.length; for(int i = 0; i < length;i++){ int indexOfLastSmall = getIndexOfLastSmall(arr,i); if(arr[i] > arr[indexOfLastSmall]){ swap(arr,i,indexOfLastSmall); printArr(arr); } } } public static int getIndexOfLastSmall(int[] arr,int start){ int length = arr.length; int smallest = arr[start]; int indexOfLastSmall = start; for(int i = start + 1; i<length;i++){ if(arr[i] < smallest){ smallest = arr[i]; indexOfLastSmall = i; } } return indexOfLastSmall; } public static void swap(int[] arr, int left,int right){ int temp = arr[left]; arr[left] = arr[right]; arr[right] = temp; } public static void printArr(int[] arr){ for(int i=0;i<arr.length;i++){ System.out.print(arr[i] + " "); } System.out.println(); } }
在上述的排序过程中,我们可以发现一个规律:为了在 k 个选项中找到最小的数字,我们需要进行 k - 1 次比较。
假设数组中有 n 个数字:
...依此类推......直到最后一步,在两个数字中找出最小的一个,我们进行了1次比较。
我们可以设步数为 j,设数组的长度为 n,在每一步的比较中,我们将会在 n - j + 1 个数字里面进行 n - j 次比较,找到这些数字里面最小的数字。
综上所述,我们可以得到如下的公式:
排序过程总比较次数 = 1 + 2 + 3 + ... + (n - 1) = (1/2) * n * (n-1) ≈ (1/2) * n2
从上面的公式可以得知,选择排序算法的时间复杂度为 O(n2),n2 前面的系数并不重要,因为 n2 才是对次数增长起决定性作用的。
那么,如果进行排序前的数组已经是排好顺序的了,会不会提升排序算法的效率呢?
答案是否定的。有兴趣的可以动手试试,你会看到不管给出的数组是否有序,选择排序算法都需要一样多的比较次数。
选择排序属于 "in place" 排序,即就地排序,因为它不需要额外的内存空间。
标签:class oid ++ sts 提升 时间 sel 步骤 src
原文地址:http://www.cnblogs.com/yartar/p/6716350.html