ML(5):KNN算法

标签：round   获取   模型   中间   学习   位置   表示   绿色   归类   

      K近邻算法，即K-Nearest Neighbor algorithm，简称KNN算法，可以简单的理解为由那离自己最近的K个点来投票决定待分类数据归为哪一类。这个算法是机器学习里面一个比较经典的算法， 总体来说KNN算法是相对比较容易理解的算法。其中的K表示最接近自己的K个数据样本。KNN算法和K-Means算法不同的是，K-Means算法用来聚类，用来判断哪些东西是一个比较相近的类型，而KNN算法是用来做归类的，也就是说，有一个样本空间里的样本分成几个类型，然后，给定一个待分类的数据，通过计算接近自己最近的K个样本来判断这个待分类数据属于哪个分类。

目录：

• 算法概述
• 工作原理
• K值的选择
• 归一化处理
• knn R示例
• 推测车型代码

算法概述

•   
• 如上图所示，有两类不同的样本数据，分别用蓝色的小正方形和红色的小三角形表示，而图正中间的那个绿色的圆所标示的数据则是待分类的数据。也就是说，现在，我们不知道中间那个绿色的数据是从属于哪一类（蓝色小正方形or红色小三角形），我们就要解决这个问题：给这个绿色的圆分类

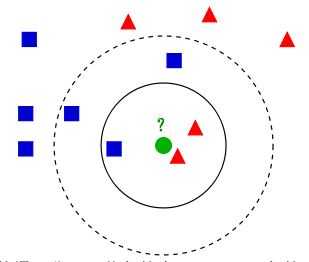
• 从上图中，你还能看到：如果K=3，绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类。

• 如果K=5，绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类
• 于此我们看到，当无法判定当前待分类点是从属于已知分类中的哪一类时，我们可以依据统计学的理论看它所处的位置特征，衡量它周围邻居的权重，而把它归为(或分配)到权重更大的那一类。这就是K近邻算法的核心思想

工作原理

• 我们知道样本集中每一个数据与所属分类的对应关系，输入没有标签的新数据后，将新数据与训练集的数据对应特征进行比较，找出“距离”最近的k数据，选择这k个数据中出现最多的分类作为新数据的分类。
• 算法描述

1. 1. 计算已知数据集中的点与当前点的距离
   2. 按距离递增次序排序
   3. 选取与当前数据点距离最近的K个点
   4. 确定前K个点所在类别出现的频率
   5. 返回频率最高的类别作为当前类别的预测

• 距离计算方法有"euclidean"（欧氏距离）,”minkowski”（明科夫斯基距离）, "maximum"（切比雪夫距离）, "manhattan"（绝对值距离）,"canberra"（兰式距离）, 或 "minkowski"（马氏距离）等
• knn算法中判断两条记录的相似度的采用的是欧式距离
• 算法缺点：

1. 1. k值需要预先设定，而不能自适应
   2. 样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数

K值的选择

• 除了如何定义邻居的问题之外，还有一个选择多少个邻居，即K值定义为多大的问题。不要小看了这个K值选择问题，因为它对K近邻算法的结果会产生重大影响。
• 如果选择较小的K值，就相当于用较小的领域中的训练实例进行预测，“学习”近似误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是“学习”的估计误差会增大，换句话说，K值的减小就意味着整体模型变得复杂，容易发生过拟合；
• 如果选择较大的K值，就相当于用较大领域中的训练实例进行预测，其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测器作用，使预测发生错误，且K值的增大就意味着整体的模型变得简单。
• 在实际应用中，K值一般取一个比较小的数值，例如采用交叉验证法（简单来说，就是一部分样本做训练集，一部分做测试集）来选择最优的K值。
• 一般来说，k的取值最好是数据集的条数开方，并且最好取奇数，?下面示例中iris是150条数据，所以这里k值选13。

归一化处理

• 数据标准化（归一化）处理是数据挖掘的一项基础工作，不同评价指标往往具有不同的量纲和量纲单位，这样的情况会影响到数据分析的结果，为了消除指标之间的量纲影响，需要进行数据标准化处理，以解决数据指标之间的可比性。原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。以下是两种常用的归一化方法：
• min-max标准化（Min-Max Normalization）：也称为离差标准化，是对原始数据的线性变换，使结果值映射到[0 - 1]之间。转换函数如下：

1. 1. 
   2. 其中max为样本数据的最大值，min为样本数据的最小值。这种方法有个缺陷就是当有新数据加入时，可能导致max和min的变化，需要重新定义。

• Z-score标准化方法: 这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1，转化函数为：

1. 1. 
   2. 其中为所有样本数据的均值，为所有样本数据的标准差。

R示例

• R实现时，可选择class包，也可选择kknn包进行计算
• 以iris为例示例代码如下：
  

  #---------------------R：KNN算法--------------------------------
  head(iris)
  a<-iris[-5] #将标记种类的列去掉
  head(a)
  a<-scale(a) #z-score标准化
  str(a)
  head(a)
  
  train<-a[c(1:25,50:75,100:125),] #训练集
  head(train)
  test<-a[c(26:49,76:99,126:150),]  #测试集
  
  #接下来需要把训练集和测试集的种类标记保存下来
  train_lab <-iris[c(1:25,50:75,100:125),5]
  test_lab <-iris[c(26:49,76:99,126:150),5]
  
  #KNN分类例子中在R中使用到的包有“class包”，“gmodels包”
  #install.packages("class")
  library(class)
  #接下来就可以调用knn函数进行模型的建立了
  ## 数据框，K个近邻投票,欧氏距离
  pre_result<-knn(train=train,test=test,cl=train_lab,k=13)
  table(pre_result,test_lab)
  
  #---------------------R：KKNN 包--------------------------------
  
  #install.packages("kknn")
  library(kknn)
  data("iris")
  dim(iris)
  m <-(dim(iris))[1]
  ind <- sample(2, m, replace=TRUE, prob=c(0.7, 0.3))
  iris.train <- iris[ind==1,]
  iris.test <- iris[ind==2,]
  
  #调用kknn  之前首先定义公式
  #myformula ：Species ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width
  iris.kknn<-kknn(Species~.,iris.train,iris.test,distance=1,kernel="triangular")
  summary(iris.kknn)
  
  # 获取fitted.values
  fit <- fitted(iris.kknn)
  
  # 建立表格检验判类准确性
  table(fit,iris.test$Species)
  
  # 绘画散点图，k-nearest neighbor用红色高亮显示
  pcol <- as.character(as.numeric(iris.test$Species))
  
  pairs(iris.test[1:4], pch = pcol, col = c("green3", "red")[(iris.test$Species != fit)+1])
        
  
  
              

  View Code

推测车型代码

• 完整代码如下：

  setwd("E:\\RML")
  cars <- read.csv("bus01.csv",header=TRUE,stringsAsFactors=TRUE)
  
  #
  library(kknn)
  m <-(dim(cars))[1]
  ind <- sample(2, m, replace=TRUE, prob=c(0.7, 0.3))
  car.train <- cars[ind==1,]
  car.test <- cars[ind==2,]
  
  #调用kknn  之前首先定义公式
  myformula <- Type ~ V + A + SOC + MinV + MaxV + MaxT + MinT
  car.kknn<-kknn(myformula,car.train,car.test,distance=1,kernel="triangular")
  
  
  # 获取car.values
  fit <- fitted(car.kknn)
  
  # 建立表格检验判类准确性
  table(fit,car.test$Type,dnn = c("predict","actual"))
  
  # 绘画散点图，k-nearest neighbor用红色高亮显示
  pcol <- as.character(as.numeric(car.test$Type))
  pairs(car.test[-8], pch = pcol, col = c("green3", "red")[(car.test$Type != fit)+1])

• 结果如下：
• 
• 图形分布
• 

ML(5):KNN算法

标签：round   获取   模型   中间   学习   位置   表示   绿色   归类   

原文地址：http://www.cnblogs.com/tgzhu/p/6699365.html