标签:gets 红色 family bit 计算 虚线 ref boolean 固定高度
1,昨天看到了一个挺好的ui效果,是使用贝塞尔曲线实现的,就和大家来分享分享,还有,在写博客的时候我经常会把自己在做某种效果时的一些问题给写出来,而不是像很多文章直接就给出了解决方法,这里给大家解释一下,这里写出我遇到的一些问题不是为了凑整片文章的字数,而是希望大家能从根源下知道它是怎么解决的,而不是你直接百度搜索这个问题解决的代码,好了,说了这么多,只是想告诉大家,我后面会在过程中提很多问题(邪恶脸,嘿嘿嘿),好吧,来看看今天的效果:
2,what is the fuck?,这就是你说的很好看的效果?各位看官别着急,这里小弟也没办法,实在是找不到好的UI图,就只能请各位将就一下了,好了言归正传,当我们看到这种效果的时候,我们已经有了一些思路,如下:
1,使用paint绘制正弦函数(调用Math.sin(x)的方法) 2,使用逐帧动画来实现 3,使用贝塞尔三阶来实现波浪效果
可能大家还有更多更好的方法,这上面几点只是我能想到的几点方法,我今天是使用的贝塞尔来实现的,不清楚贝塞尔使用的同学可以在我博客分类的系列中找到这一栏的分类。
OK,我们先不要去管那些动画,我们一步一步的来,那么我们的视图就只有两部分了,一个是粉红色带水区域,一个是我们中间随着动的icon图片,那我们先来实现第一个粉红色带水的地方,我们最后要实现的效果如下:
ok,为了我们控件的扩展性,我们这里自定义一些属性,这里我们同学可以先不要理解这一块(等全部理解之后再来看这一块)
<?xml version="1.0" encoding="utf-8"?>
<resources>
<declare-styleable name="WaveView">
<!--中间小船的图片-->
<attr name="imageBitmap" format="reference"></attr>
<!--水位是否要上升-->
<attr name="rise" format="boolean"></attr>
<!--水波纹向右移动的时候执行的时间-->
<attr name="duration" format="integer"></attr>
<!--起始点的Y坐标-->
<attr name="originY" format="integer"></attr>
<!--水波纹的高度-->
<attr name="waveHeight" format="integer"></attr>
<!--水波纹的长度-->
<attr name="waveLength" format="integer"></attr>
</declare-styleable>
</resources>
创建一个WaveView类,继承自View,并初始化一些自定义属性,这里两个重要的属性一个是一个正弦的最高点,即我们的水波纹的高度;一个是我们一个正弦的长度,即我们一个水波纹的横坐标的长度,下面是一些属性的初始化 ,很简单,没什么难的
//中间小船图片的引用
private int imageBitmap;
//小船实际的bitmap
private Bitmap bitmap;
//是否上升水位
private boolean rise;
//水位起始点
private int originY;
//波纹平移的执行的时间
private int duration;
//波纹的宽度
private int waveWidth;
//波纹的高度
private int waveHeight;
//画笔
private Paint mPaint;
//路径
private Path mPath;
//控件的宽度高度
private int width;
private int height;
public WaveView(Context context) {
this(context, null);
}
public WaveView(Context context, @Nullable AttributeSet attrs) {
this(context, attrs, 0);
}
public WaveView(Context context, @Nullable AttributeSet attrs, int defStyleAttr) {
super(context, attrs, defStyleAttr);
init(context, attrs, defStyleAttr);
}
private void init(Context context, AttributeSet attrs, int defStyleAttr) {
TypedArray a = context.obtainStyledAttributes(attrs, R.styleable.WaveView);
imageBitmap = a.getResourceId(R.styleable.WaveView_imageBitmap, 0);
rise = a.getBoolean(R.styleable.WaveView_rise, false);
duration = a.getInt(R.styleable.WaveView_duration, 2000);
originY = a.getInt(R.styleable.WaveView_originY, 500);
waveWidth = a.getInt(R.styleable.WaveView_waveLength, 500);
waveHeight = a.getInt(R.styleable.WaveView_waveHeight, 500);
a.recycle();
//压缩图片
BitmapFactory.Options options = new BitmapFactory.Options();
options.inSampleSize = 2; //压缩图片倍数
if (imageBitmap > 0) {
bitmap = BitmapFactory.decodeResource(getResources(), imageBitmap,options);
} else {
bitmap = BitmapFactory.decodeResource(getResources(), R.mipmap.ic_launcher, options);
}
//初始化画笔
mPaint = new Paint();
mPaint.setColor(getResources().getColor(R.color.colorAccent));
mPaint.setAntiAlias(true);
mPaint.setStyle(Paint.Style.FILL_AND_STROKE);
//初始化路径
mPath = new Path();
}
然后重写OnMeasure中测量我们空间的高度,这里基本上是使用系统测量的宽高度,就是在height为wrap_content的时候设置了800px,这里的代码也很简单,不多解释,直接上代码
@Override
protected void onMeasure(int widthMeasureSpec, int heightMeasureSpec) {
super.onMeasure(widthMeasureSpec, heightMeasureSpec);
int widthMode = MeasureSpec.getMode(widthMeasureSpec); //获取宽的模式
int heightMode = MeasureSpec.getMode(heightMeasureSpec); // 获取高的模式
int widthSize = MeasureSpec.getSize(widthMeasureSpec); //获取宽的尺寸
int heightSize = MeasureSpec.getSize(heightMeasureSpec); //获取高的尺寸
if (widthMode == MeasureSpec.EXACTLY) {
width = widthSize;
}
if (heightMode == MeasureSpec.EXACTLY) {
height = heightSize;
} else {
height = 800;
}
//保存丈量结果
setMeasuredDimension(width, height);
}
继续,重写OnDraw方法,注意了,这是今天整篇博客重点的地方,首先我们知道要使用贝塞尔三阶来实现,所以我们可以基本上写出如下的代码:
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
//不断的计算波浪的路径
calculatePath();
//绘制水部分
canvas.drawPath(mPath, mPaint);
}
关键是我们calculatePath()方法中的逻辑处理,这是直接使用贝塞尔,首先我们把我们的绘制起始点平移到我们自定义originY属性的位置
mPath.moveTo(0, originY);
然后在通过我们的width长度和waveHeight的长度来判断,到底在屏幕中绘制多少个正弦曲线
for (int i = -waveWidth; i < width + waveWidth; i += waveWidth) {
//利用三阶贝塞尔曲线绘制
mPath.rCubicTo(????);
}
OK,这里我们绘制整体的思路没什么问题了,关键我们三阶贝塞尔曲线的两个控制点和一个结束点的坐标的确认了(这里压根不知道什么是控制点和结束点的同学整真的推荐你先去看看我博客的贝塞尔基础知识了)
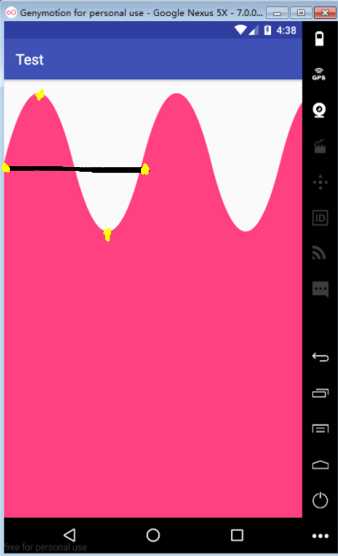
这里请大家看我在上图中标注的四个点就分别是我们的起始点、控制点1、控制点2、结束点,ok,所以我们可以写成如下的代码:
mPath.moveTo(0, originY);
//绘制波浪
for (int i = -waveWidth; i < width + waveWidth; i += waveWidth) {
//利用三阶贝塞尔曲线绘制
mPath.rCubicTo(waveWidth / 4, -waveHeight, waveWidth / 4 * 3, waveHeight, waveWidth, 0);
}
ok,写到这里了我们就可以看一下我们的贝塞尔三阶的效果了,效果图如下:
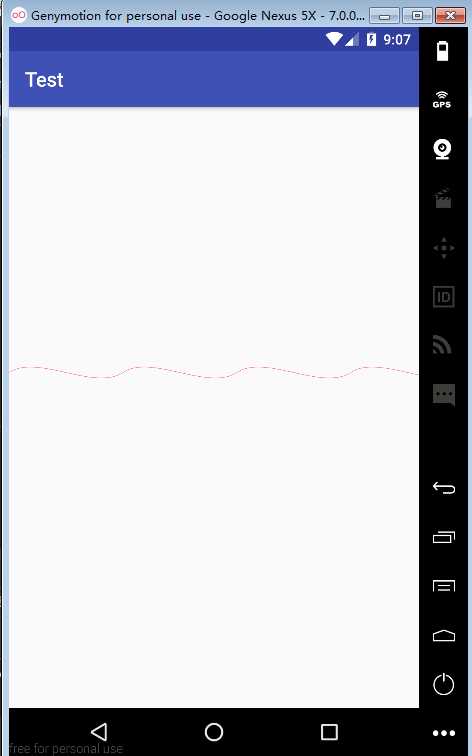
绘制的曲线有点淡,不过还是绘制出来了,但是感觉这里的三阶绘制的曲线和我们想象中的正弦虚线还是有些差距的,我们将三阶换成两个二阶试试
mPath.moveTo(0, originY);
//绘制波浪
for (int i = -waveWidth; i < width + waveWidth; i += waveWidth) {
//利用三阶贝塞尔曲线绘制
// mPath.rCubicTo(waveWidth / 4, -waveHeight, waveWidth / 4 * 3, waveHeight, waveWidth, 0);
//利用二阶贝塞尔曲线绘制
mPath.rQuadTo(waveWidth / 4, -waveHeight, waveWidth / 2, 0);
mPath.rQuadTo(waveWidth / 4, waveHeight, waveWidth / 2, 0);
}
效果图如下:
ok,没问题,这样的话就和要的效果差不多了,我们继续要实现下面的水是填充满的那么我们还需要绘制一下这三线(下图黄色的标记的),这样才能组成一个封闭的区域。
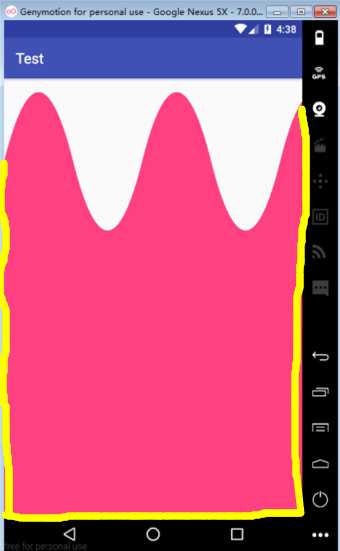
逻辑很简单,我就直接上代码了
//绘制连线
mPath.lineTo(width, height);
mPath.lineTo(0, height);
mPath.close();
再看一下效果图
没问题,到这里我们已经成功了我们今天任务的三分之一了,我们接着实现,现在我们想着的是怎么才能让我们的水波纹动起来,这里肯定有同学会说,那肯定属性动画啊,对的,没错,是使用属性动画,但是,怎么使用?在哪里使用是一个问题(第一个难点来了)!!
这里我想的思路是改变我们绘制波长的起始坐标,设置(-waveWidth,originY)为其实坐标,为什么这样来呢?因为我们打算最左边多绘制一个波长的水(这里有个bug,所以也要在最右边多绘制一个波长,具体解释看下图中的标注),然后通过属性动画平移(且不但重复平移一个周长的长度),这样就可以达到我们的动画效果,

所以代码修改成了如下:
mPath.moveTo(-waveWidth + dx, originY);
for (int i = -waveWidth; i < width + waveWidth; i += waveWidth) {
//利用三阶贝塞尔曲线绘制
// mPath.rCubicTo(waveWidth / 4, -waveHeight, waveWidth / 4 * 3, waveHeight, waveWidth, 0);
//利用二阶贝塞尔曲线绘制
mPath.rQuadTo(waveWidth / 4, -waveHeight, waveWidth / 2, 0);
mPath.rQuadTo(waveWidth / 4, waveHeight, waveWidth / 2, 0);
}
//绘制连线
mPath.lineTo(width, height);
mPath.lineTo(0, height);
mPath.close();
ok,这样我们下面在编写一个简单的动画,动态的改变dx的值,从而改变我们动画向右移动(这里涉及到属性动画,不过里面的知识都是最基础的,大家应该能看懂)
//开始动画
public void startAnimation() {
animator = ValueAnimator.ofFloat(0, 1);
animator.setDuration(duration);
animator.setRepeatCount(ValueAnimator.INFINITE);
animator.setInterpolator(new LinearInterpolator());
animator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
@Override
public void onAnimationUpdate(ValueAnimator animation) {
float fraction = (float) animation.getAnimatedValue();
dx = (int) (waveWidth * fraction);
postInvalidate();
}
});
animator.start();
}
ok,在这里我们就可以看一下我们的动画效果了,别忘记了在Activity中去调用
mWaveView = (WaveView)findViewById(R.id.waveview);
mWaveView.startAnimation();
ok,这样我们下面的水波纹就搞定了,这样我们就差不多完成了二分之一了,我们继续,现在差的就是绘制我们的小船了,先随便找个点先把小船搞出来,再在后面慢慢的考虑它安放的具体位置,这里我先写个固定高度800
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
//不断的计算波浪的路径
calculatePath();
//绘制水部分
canvas.drawPath(mPath, mPaint);
//绘制小船部分
canvas.drawBitmap(bitmap,width/2,800,mPaint);
}
看一下效果
图片倒是展示出来了,现在就是怎么样让他随着波浪上下滚动,有些同学可能就会说,阿呆哥哥啊 ,很简单啊,也是很明显x坐标是固定的,就是width的一般,Y坐标就是挨着它波浪的高度,直接搞个属性动画,随着波浪高度的改变而改变呗。
恩,关键是挨着它的那个波浪的那个坐标该怎么计算,这是问题的关键点(这是我们实现这个效果的第二个困难点)
这里提供一个思路,我们绘制一条中垂线,即下图这条蓝色的线和每次我们水波纹相交的点就是我们小船图片的放置点
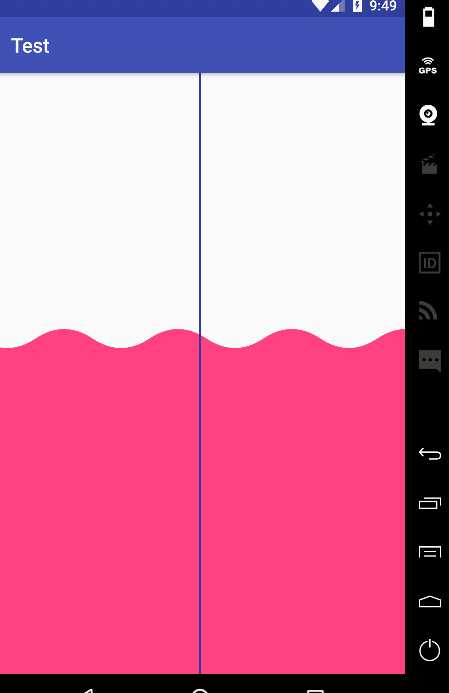
现在思路清晰了,现在就是要找到这个交点,那么Android中Path类中有没有方法是可以拿到这个值得呢? 很明确的告诉你没有,现在到这里我们的思路又断了,但是我告诉大家这里有一个Region类可以代替的实现这种效果(由于篇幅已经很长了,这就就不和大家详细介绍Region类的),这个类的解释就是获取两个区域的交集区域,例如:图下的小矩形区域就是我们大的矩形和水波纹的交集区域
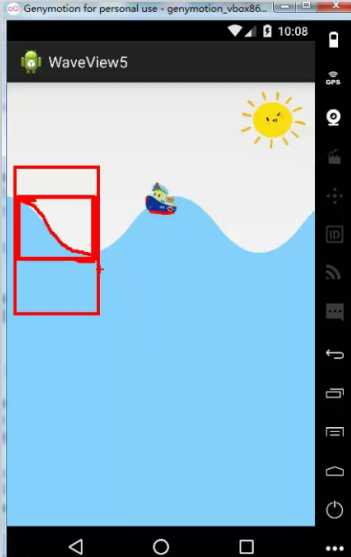
我们按照数学的极限思想来想一下,当这里我们外面大的矩形区域左右坐标无线接近的时候我们矩形就可以看做是一条直线了,这样就达到了我们之前的要求了
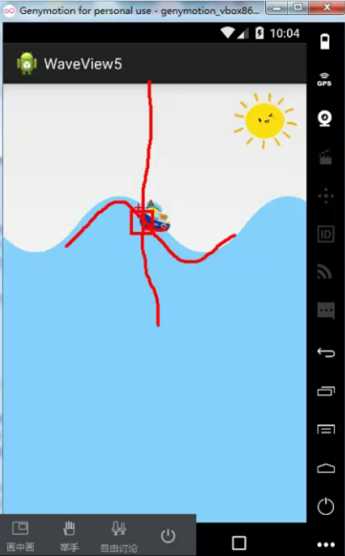
思路就很清晰了,我们来看代码
float x = width / 2;
region = new Region();
Region clip = new Region((int) (x - 0.1), 0, (int) x, height);
region.setPath(mPath, clip);
这里要提醒一下,一定要放在绘制贝塞尔曲线之后、绘制其它三条线之前(这是一个坑,大家要注意一下)
再看看拿到矩形区域并设置图片的坐标(这里我直接取得这个矩形的有坐标和上坐标)
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
//不断的计算波浪的路径
calculatePath();
//绘制水部分
canvas.drawPath(mPath, mPaint);
//获取当前小船应该在的地方
Rect rect = region.getBounds();
canvas.drawBitmap(bitmap, rect.right, rect.top, mPaint);
}
看一下效果
效果大致出来了,可能有些同学说,这是因为bitmap的起始点不是他的中心点,那么我们继续修改修改
canvas.drawBitmap(bitmap, rect.right - (bitmap.getWidth()/2), rect.top-(bitmap.getHeight()/2), mPaint);
再看看效果
这时候看起来舒服多了,大致的偏差没什么问题了,但是在波谷的时候还是有一点问题,这是什么原因呢,这里呢,我们还是有点偏差的,当Y坐标大于originY的时候,我们这里使用rect.bottom拿到的值会更精确一些;当Y坐标小于originY的时候,我们这里使用rect.top拿到的值会更精确一些(大家认真的思考一下,这里其实很好懂得)
//获取当前小船应该在的地方
Rect rect = region.getBounds();
Log.i("wangjitao", "right:" + rect.right + ",top:" + rect.bottom);
if (rect.top < originY){
canvas.drawBitmap(bitmap, rect.right - (bitmap.getWidth()/2), rect.top-(bitmap.getHeight()/2), mPaint);
}else {
canvas.drawBitmap(bitmap, rect.right - (bitmap.getWidth()/2), rect.bottom-(bitmap.getHeight()/2), mPaint);
}
效果如下:
ok,现在我们的坐标就完全正确了,没问题了,搞定
其实这里还有更好扩展的小效果,如下:
1,提供刚进来的时候涨水效果 2,船水波纹飘动的时候,船的方向也随着波纹的切线平行(这里就要使用到sin 的求导,可以我忘记完了)
这些功能在这里就不和大家实现了,大家可以下去自己实现,今天有晚了,不过干货还是挺多的,希望大家好好理解,特别是我们遇到问题时候该怎么解决,这个很关键。不多说了,睡觉了。See You Next Time.........
标签:gets 红色 family bit 计算 虚线 ref boolean 固定高度
原文地址:http://www.cnblogs.com/wjtaigwh/p/6750184.html