标签：数字   小顶堆   交换   csdn   get   排序算法   ges   开始   最大   

最近面试一直问到排序，老是各种搞混，特地来整理整理

先盗用一张图：

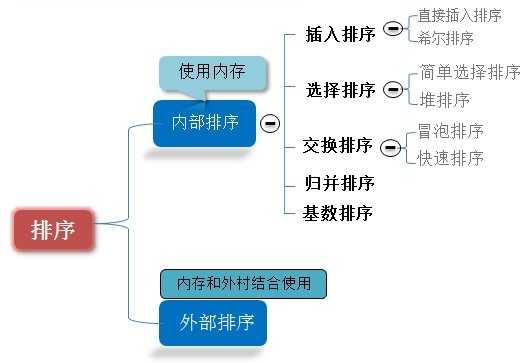
说明： 内部排序基于内存，外部排序是数据量大，而内存与外存的相结合的排序

一、插入排序

　　关键词：插入，将数字插入到一条已经排好序的有序表中。

1.1直接插入排序

　　假设要5,4，2,3,1 要升序排列。

　　i=1　　5

　　i=2　　5,4    ==>4,5

　　i=3　　4,5,2　　===>2,4,5

　　i=4　　2,4,5,3　　==>2,3,4,5

　　...

　　思想很简单，就是从一个元素开始，一个个元素添加，返回有序列表。

　　其复杂度为   1+2+3+。。+n = O(n²)

1.2希尔排序

　　希尔排序是直接排序的一个加强版，我们知道直接排序前，要排序的序列有一定的序列特性，则需要移动的次数减少，效率提高。

　　如，要排序的序列为5,4,3,2，1 与序列 1,2,5,4,3,相比，运用直接排序，后者将移动较小的次数。

　　希尔排序的基本思想是：

　　把记录按步长 gap 分组，对每组记录采用直接插入排序方法进行排序。
　　随着步长逐渐减小，所分成的组包含的记录越来越多，当步长的值减小到 1 时，整个数据合成为一组，构成一组有序记录，则完成排序。

　　我们来通过演示图，更深入的理解一下这个过程。 

　　希尔排序是一种不稳定的排序：其平均复杂度为 O(Nlog2N)

　　具体大家可以参考：http://www.cnblogs.com/jingmoxukong/p/4303279.html

二、选择排序

　　关键词：选择，选择最小的与第一个交换，剩下的最小与第二个交换，一次类推

2.1简单选择排序

　　选择最小的与第一个交换，剩下的最小与第二个交换，。。。。

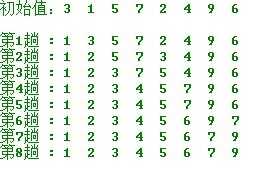
　　比较稳定的排序，时间复杂度为：n+(n-1)+..+1 = O(n²)

2.2堆排序

堆的定义如下：具有n个元素的序列（k1,k2,...,kn),当且仅当满足

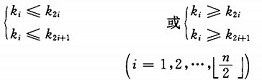
时称之为堆。由堆的定义可以看出，堆顶元素（即第一个元素）必为最小项（小顶堆）。
若以一维数组存储一个堆，则堆对应一棵完全二叉树，且所有非叶结点的值均不大于(或不小于)其子女的值，根结点（堆顶元素）的值是最小(或最大)的。如：

（a）大顶堆序列：（96, 83,27,38,11,09)

  (b)  小顶堆序列：（12，36，24，85，47，30，53，91）

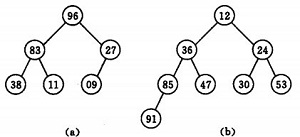
　　可以看出堆排序本质也是选择排序，以最小堆为例，堆顶元素为最小值，输出最小值，并将最后一个元素提至堆顶（蓄意破坏堆结构），则重新构建最小堆后，堆顶又是最小值，以此内推。

　　堆排序也是一种不稳定的排序，其在最坏的情况下复杂度为O(nlogn)

三、交换排序

　　关键词：交换

　　未完待续：

参考：http://blog.csdn.net/hguisu/article/details/7776068

多种排序算法整理

标签：数字   小顶堆   交换   csdn   get   排序算法   ges   开始   最大   

原文地址：http://www.cnblogs.com/yanyouqiang/p/6754227.html