标签:class img alt length main pre print nod com
public class Dijkstra {
private static int N = 1000;
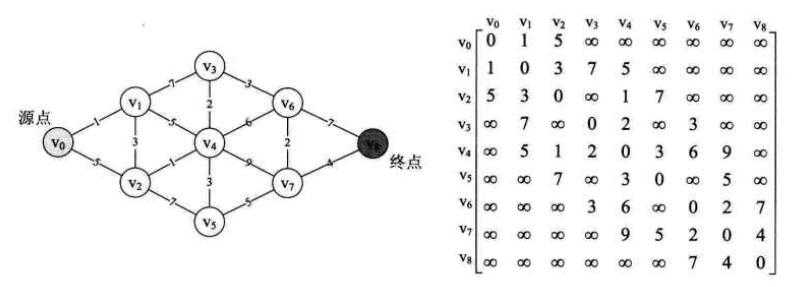
private static int[][] Graph = {
{ 0, 1, 5, N, N, N, N, N, N },
{ 1, 0, 3, 7, 5, N, N, N, N },
{ 5, 3, 0, N, 1, 7, N, N, N },
{ N, 7, N, 0, 2, N, 3, N, N },
{ N, 5, 1, 2, 0, 3, 6, 9, N },
{ N, N, 7, N, 3, 0, N, 5, N },
{ N, N, N, 3, 6, N, 0, 2, 7 },
{ N, N, N, N, 9, 5, 2, 0, 4 },
{ N, N, N, N, N, N, 7, 4, 0 } };
public static void main(String[] args) {
dijkstra(0, Graph);
}
/**
* Dijkstra最短路径。
* 即图中"节点vs"到其它各个节点的最短路径。
* @param vs 起始节点
* @param Graph 图
*/
public static void dijkstra(int vs, int[][] Graph) {
int NUM = Graph[0].length;
// 前驱节点数组
int[] prenode = new int[NUM];
// 最短距离数组
int[] mindist = new int[NUM];
// 该节点是否已经找到最短路径
boolean[] find = new boolean[NUM];
int vnear = 0;
for (int i = 0; i < mindist.length; i++) {
prenode[i] = i;
mindist[i] = Graph[vs][i];
find[i] = false;
}
find[vs] = true;
for (int v = 1; v < Graph.length; v++) {
// 每次循环求得距离vs最近的节点vnear和最短距离min
int min = N;
for (int j = 0; j < Graph.length; j++) {
if (!find[j] && mindist[j] < min) {
min = mindist[j];
vnear = j;
}
}
find[vnear] = true;
// 根据vnear修正vs到其他所有节点的前驱节点及距离
for (int k = 0; k < Graph.length; k++) {
if (!find[k] && (min + Graph[vnear][k]) < mindist[k]) {
prenode[k] = vnear;
mindist[k] = min + Graph[vnear][k];
}
}
}
for (int i = 0; i < NUM; i++) {
System.out.println("v" + vs + "...v" + prenode[i] + "->v" + i + ", s=" + mindist[i]);
}
}
标签:class img alt length main pre print nod com
原文地址:http://www.cnblogs.com/zengzhihua/p/6755439.html