标签:mda 等于 第一个 插入排序 .com 基本 src 部分 快速排序
内部排序:数据全部在内存中进行排序
外部排序:数据量太大,不能一次在内存中进行排序,因此,在排序的过程中需要使用到外部存储介质
将一个数据插入到已经有序的序列中得到一个新的有序序列
思路:从第二个元素开始进行插入排序
将序列分成多个子序列分别进行直接插入排序,待整个序列基本有序时,再对整体序列进行直接插入排序。
核心是分组
分组策略一般采用增量分组策略,d = {n/2 ,n/4, n/8 .....1} n元素的个数,d为要分组元素的间隔
比如:2, 5, 4, 3, n = 4, 第一趟d = n / 2 = 4 / 2 = 2,分组为 [2, 4], [5, 3]
基本思想
从小到大:从待排序的序列中选择一个最小的数与第一个位置交换,然后在剩余的数中选择一个最小的数据与第二个位置交换,依次类推,直到倒数第二个数与倒数第一个数进行比较交换位置为止。
基本思想从小到大:从待排序的序列中每次找出最小的数和最大的数分别与第一个元素和最后一个元素进行位置交换,然后在剩余的数中继续找出最小的数和最大的数分别与第二个元素和倒数第二个元素进行位置交换。依次类推,直到剩余的数为1或者为0位置。
树形选择排序
堆定义:树的子节点必须都比父节点大或者小,因此,分为大顶堆和小顶堆
排序思想
初始时把待排序的n个元素的序列看成是顺序存储的二叉树(一维数组存储二叉树)。调整序列中元素的顺序使它们成为一个堆,此时,将堆顶的元素取出,那么将会得到n个元素中最小的(最大的)元素。然后,对剩余的n-1元素重新构建成一个堆,那么将会得到剩余n-1个元素中最小的(最大的)元素,依次类推,直到剩余2个元素的堆,对它们进行比较交换。
堆排序的两个主要问题:
1、将n个元素构建成堆
2、对剩余的元素如和构建成新的堆
调整小顶堆的方法:
1、假设n个元素,输出一个堆顶元素还剩n-1个元素,将堆中最后一个元素放入到堆顶元素所在的位置
2、将堆顶节点与左右节点进行比较,选择最小的节点与堆顶节点进行交换
3、如果交换后还是破坏了堆结构,则重复2,直到交换到叶子节点位置为止
构建小顶堆
1、假设n个元素,这n个元素构成一个二叉树,但是不一定是堆,此时,如果把该树的叶子节点看做树的话,是符合堆的
2、寻找一个叶子节点,然后,从该叶子节点开始调整,直到整个树符合堆结构
寻找创建堆节点的位置:(n - 1) / 2这个位置的节点要么是叶子节点,要么是叶子节点的父节点
假设序列为 (5 3 4 1 6),奇数个元素
二叉树结构为
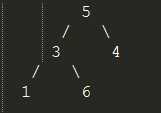
(n - 1) / 2 = (5 - 1) / 2 = 2, 则下标为2的元素为4,此时,4为叶子节点,可以从4这个节点进行调整
假设序列为 (5 3 4 1 6 12) ,偶数个元素
二叉树结构为
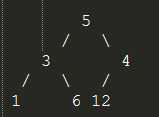
(n - 1) / 2 = (6 - 1) / 2 = 2, 则下标为2的元素为4,4为叶子节点的父节点,从4这个节点开始调整
基本思想
从大到小排序:临近的元素进行两两比较,如果前面的小于后面的则交换位置。如此,进行多趟(n - 1),则序列有序
第一种:加一个标志变量,记录某一趟排序是否进行了数据位置的交换,如果没有则代表已经有序,则需要停止排序
第二种:每趟排序进行正反两个方向的冒泡,一趟冒泡可以得到最大值和最小值
基本思想
1、选择一个基准元素,通常选择第一个或者最后一个元素
2、通过一趟排序,将序列分成两部分,一部分大于基准元素,另外一部分小于基准元素
3、此时,基准元素已经在它正确的位置上了
4、对分成的两部分进行同样的操作,依次类推,直到整个序列有序
基本思想
将两个或者两个以上的有序序列合并成一个有序序列。
将待排序序列R[0...n-1]看成是n个长度为1的有序序列,将相邻的有序序列成对归并,得到n/2个长度为2的有序序列;将这些有序序列再次归并,得到n/4个长度为4的有序序列;如此反复进行下去,最后得到一个长度为n的有序序列
合并思想
在每次合并过程中,都是对两个有序的序列进行合并,这两个有序序列分别为R[low, mid]和R[mid+1, high]。先将他们合并到一个局部的暂存数组R2中,待合并完成后再将R2复制回R中。为了方便描述,我们称 R[low, mid] 第一段,R[mid+1, high] 为第二段。每次从两个段中取出一个记录进行比较,将较小者放入R2中。最后将各段中余下的部分直接复制到R2中。经过这样的过程,R2已经是一个有序的序列,再将其复制回R中,一次合并排序就完成了。
算法思想
把数据进行分桶,分桶后桶和桶之间的数据是有序的,也就是说前一个桶中的最大值小于等于后一个桶中的最小值,然后对每个桶中的数据进行排序,最后,把所有桶中的数据收集到一块,则此时数据已经排好序了。
基数排序
是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以是稳定的。
标签:mda 等于 第一个 插入排序 .com 基本 src 部分 快速排序
原文地址:http://www.cnblogs.com/heml/p/6803179.html