标签:条件 没有 img 放大 label 利用 赋值运算 参数 公式
4.1布尔逻辑
布尔比较运算符
== != < > <= >=
处理布尔值的布尔值运算符
! & | ^(异或)
条件布尔运算符
&& || 比&和|性能更好 比如&&只需判断前面的布尔值为false,整体值就为false,不用计算后面的布尔值
1.布尔赋值运算符
&= |= ^=
2.按位运算符
& | ^ ~
位移运算符 >> <<
位移赋值运算符>>= <<=
3.运算符优先级(更新)
++,--(用作前缀);(),+,-(一元),!,~
*,/,%
+,-
<<,>>
<,>,<=,>=
==,!=
&
^
|
&&
||
=,*=,/=,%=,+=,-=,>>=,<<=,&=,^=,|=赋值运算符
++,--(用作后缀)
4.2 goto语句
goto <labelName>
4.3 分支
1.三元运算符
? :
2.if语句
if(){}else{}
3.switch语句
switch()
{
case val1:……;break;
case val2:……;break;
……
default:如果没有匹配的val值,有default,执行default中的代码
}
声明常量:指定变量类型和关键字const,同时必须给它们赋值。
4.4.循环:重复执行语句
1.do循环
do
{先执行一次判断while()内的值,为true则再次执行,false退出循环
}while();
2.while循环
while(){}先判断while()内的值,true才开始执行
3.for循环
for(int i=0;i<4,i++){}
4.循环中断
break:立即终止循环
continue:立即终止当前循环,进入下一次循环
goto:跳出循环到指定标记位置上
return:跳出循环及包含该循环的函数
5.无限循环
while(true){} 利用break等退出
Mandelbrot集合示例(书中给出的示例代码用C#)
class Program { //Mandelbrot图像中的每个位置都对应于公式N=x+y*i中的一个复数。其实数部分是x,虚数部分是y,i是-1的平方根。图像中各个位置的x和y坐标对应于虚数的x和y部分 //图像中的每个位置用参数N来表示,它是x*x+y*y的平方根。如果这个值大于或等于2,则这个数字对应的位置值是0。如果参数N的值小于2,就把N的值改为N*N-N(N=(x* x-y* y-x)+(2*x* y-y)*i)),并再次测试这个新N值。如果这个值大于或等于2,则这个数字对应的位置值是1。这个过程一直继续下去,直到我们给图像中的位置赋一个值,或迭代执行的次数多于指定的次数为止。” static void Main(string[] args) { //N的实数和虚数部分 double realCoord, imagCoord; //存储计算过程中的临时信息 double realTemp, imagTemp, realTemp2, arg; //记录在参数N(arg)等于或大于2之前的迭代次数 int iterations; //选择合适的边界值来显示Mandelbrot图像的主要部分,如果想放大这个图像,可以放大这些边界值。 for (imagCoord = 1.2; imagCoord >= -1.2; imagCoord -= 0.05) { //两个for循环处理图像中的一个点,给N指定一个值。 for (realCoord = -0.6; realCoord <= 1.77; realCoord += 0.03) { //初始化变量 iterations = 0; realTemp = realCoord; imagTemp = imagCoord; arg = (realCoord * realCoord) + (imagCoord * imagCoord); //2是4的平方根,所以仅计算x^2+y^2的值,while循环执行迭代, while ((arg < 4) && (iterations < 40)) { //N*N-N的实数部分 realTemp2 = (realTemp * realTemp) - (imagTemp * imagTemp) - realCoord; //N*N-N的虚数部分 imagTemp = (2 * realTemp * imagTemp) - imagCoord; realTemp = realTemp2; arg = (realTemp * realTemp) + (imagTemp * imagTemp); //当前点的值存储在iterations中 iterations += 1; } //选择要输出的字符 switch (iterations % 4) { case 0: Console.Write("."); break; case 1: Console.Write("o"); break; case 2: Console.Write("O"); break; case 3: Console.Write("@"); break; } } //内层循环结束后需要结束一行,所以输出换行符。 Console.Write("\n"); } Console.ReadKey(); } }
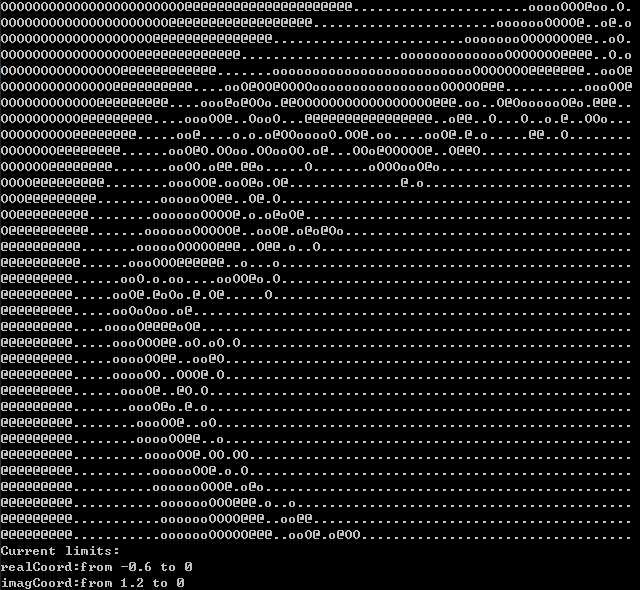
演示结果为:

章节习题要求用户输入图像的边界,并显示选中的图像部分。当前代码输出的字符应正好能放在控制台应用程序的一行上,考虑如何使每个选中的图像正好占据
大小相同的空间,以最大化可视区域。
class Program { //Mandelbrot图像中的每个位置都对应于公式N=x+y*i中的一个复数。其实数部分是x,虚数部分是y,i是-1的平方根。图像中各个位置的x和y坐标对应于虚数的x和y部分 //图像中的每个位置用参数N来表示,它是x*x+y*y的平方根。如果这个值大于或等于2,则这个数字对应的位置值是0。如果参数N的值小于2,就把N的值改为N*N-N(N=(x* x-y* y-x)+(2*x* y-y)*i)),并再次测试这个新N值。如果这个值大于或等于2,则这个数字对应的位置值是1。这个过程一直继续下去,直到我们给图像中的位置赋一个值,或迭代执行的次数多于指定的次数为止。” static void Main(string[] args) { //N的实数和虚数部分 double realCoord, imagCoord; double realMax = 1.77; double realMin = -0.6; double imagMax = -1.2; double imagMin = 1.2; double realStep; double imagStep; //存储计算过程中的临时信息 double realTemp, imagTemp, realTemp2, arg; //记录在参数N(arg)等于或大于2之前的迭代次数 int iterations; //选择合适的边界值来显示Mandelbrot图像的主要部分,如果想放大这个图像,可以放大(其实是减小)这些边界值。 while (true) { //设定跨度以保证每个选中的图像正好占据大小相同的空间,以最大化可视区域。 realStep = (realMax - realMin) / 79; imagStep = (imagMax - imagMin) / 48; for (imagCoord = imagMin; imagCoord >= imagMax; imagCoord += imagStep) { //两个for循环处理图像中的一个点,给N指定一个值。 for (realCoord = realMin; realCoord <= realMax; realCoord += realStep) { //初始化变量 iterations = 0; realTemp = realCoord; imagTemp = imagCoord; arg = (realCoord * realCoord) + (imagCoord * imagCoord); //2是4的平方根,所以仅计算x^2+y^2的值,while循环执行迭代, while ((arg < 4) && (iterations < 40)) { //N*N-N的实数部分 realTemp2 = (realTemp * realTemp) - (imagTemp * imagTemp) - realCoord; //N*N-N的虚数部分 imagTemp = (2 * realTemp * imagTemp) - imagCoord; realTemp = realTemp2; arg = (realTemp * realTemp) + (imagTemp * imagTemp); //当前点的值存储在iterations中 iterations += 1; } //选择要输出的字符 switch (iterations % 4) { case 0: Console.Write("."); break; case 1: Console.Write("o"); break; case 2: Console.Write("O"); break; case 3: Console.Write("@"); break; } } //内层循环结束后需要结束一行,所以输出换行符。 Console.Write("\n"); } //当前边界值 Console.WriteLine("Current limits:"); Console.WriteLine("realCoord:from {0} to {1} ", realMin, realMax); Console.WriteLine("imagCoord:from {0} to {1} \n", imagMin, imagMax); //输入新的边界值 Console.WriteLine("Enter new limits:"); //实数 Console.WriteLine("realCoord:from:"); realMin = Convert.ToDouble(Console.ReadLine()); Console.WriteLine("realCoord:to:"); realMax = Convert.ToDouble(Console.ReadLine()); //虚数 Console.WriteLine("imagCoord:from:"); imagMin = Convert.ToDouble(Console.ReadLine()); Console.WriteLine("imagCoord:to:"); imagMax = Convert.ToDouble(Console.ReadLine()); } } }
原边界(-0.6,1.2) (1.77,-1.2)
现边界(-0.6,1.2) (0,0)
相当于放大了原来的图像的一部分:大概是这一部分?目前只能理解到这个程度了

标签:条件 没有 img 放大 label 利用 赋值运算 参数 公式
原文地址:http://www.cnblogs.com/yuanburun/p/6808578.html