标签:tf-idf 最大 贝叶斯 向量 float 推导 sha 构造方法 概率
一. 贝叶斯公式推导
朴素贝叶斯分类是一种十分简单的分类算法,叫它朴素是因为其思想基础的简单性:就文本分类而言,它认为词袋中的两两词之间的关系是相互独立的,即一个对象 的特征向量中每个维度都是相互独立的。例如,黄色是苹果和梨共有的属性,但苹果 和梨是相互独立的。这是朴素贝叶斯理论的思想基础。现在我们将它扩展到多维的情况:
朴素贝叶斯分类的正式定义如下:
1.设 x={a1,a2,…,am}为一个待分类项,而每个 a 为 x 的一个特征属性。
2.有类别集合 C={y1,y2,…,yn}。
3.计算 P( y1|x) ,P( y2|x),…, P( yn|x)。
4.如果 P( yk|x) =max{P( y1|x),P( y2|x),…, P( yn|x)},则 x∈yk。
那么现在的关键就是如何计算第 3 步中的各个条件概率。我们可以这么做:
(1) 找到一个已知分类的待分类项集合,也就是训练集。
(2) 统计得到在各类别下各个特征属性的条件概率估计。即:
P(a1|y1) , P(a2|y1),…, P(am|y1);
P(a1|y2) , P(a2|y2),…, P(am|y2);
P(am|yn) , P(am|yn),…, P(am|yn)。
(3) 如果各个特征属性是条件独立的(或者我们假设它们之间是相互独立的),则根 据贝叶斯定理有如下推导: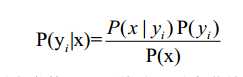
因为分母对于所有类别为常数,只要将分子最大化皆可。又因为各特征属性是条 件独立的,所以有:
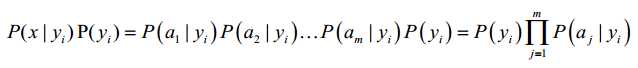
根据上述分析,朴素贝叶斯分类的流程可以表示如下: 第一阶段:训练数据生成训练样本集:TF-IDF
第二阶段:对每个类别计算 P(yi)
第三阶段:对每个特征属性计算所有划分的条件概率 第四阶段:对每个类别计算 P( x | yi ) P( yi )
第五阶段:以 P( x | yi ) P( yi ) 的最大项作为 x 的所属类别
二. 朴素贝叶斯算法实现
使用简单的英文语料作为数据集:
def loadDataSet(): postingList=[[‘my‘, ‘dog‘, ‘has‘, ‘flea‘, ‘problems‘, ‘help‘, ‘please‘], [‘maybe‘, ‘not‘, ‘take‘, ‘him‘, ‘to‘, ‘dog‘, ‘park‘, ‘stupid‘], [‘my‘, ‘dalmation‘, ‘is‘, ‘so‘, ‘cute‘, ‘I‘, ‘love‘, ‘him‘,‘my‘], [‘stop‘, ‘posting‘, ‘stupid‘, ‘worthless‘, ‘garbage‘], [‘mr‘, ‘licks‘, ‘ate‘, ‘my‘, ‘steak‘, ‘how‘, ‘to‘, ‘stop‘, ‘him‘], [‘quit‘, ‘buying‘, ‘worthless‘, ‘dog‘, ‘food‘, ‘stupid‘]] classVec = [0,1,0,1,0,1] #1 is abusive, 0 not return postingList,classVec
postList 是训练集文本,classVec 是每个文本对应的分类。
根据上节的步骤,逐步实现贝叶斯算法的全过程:
1.编写一个贝叶斯算法类,并创建默认的构造方法:
class NBayes(object): def __init__(self): self.vocabulary= [] # 词典 self.idf=0 # 词典的 idf 权值向量 self.tf=0 # 训练集的权值矩阵 self.tdm=0 # P(x|yi) self.Pcates = {} # P(yi)--是个类别字典 self.labels=[] # 对应每个文本的分类,是个外部导入的列表 self.doclength = 0 # 训练集文本数 self.vocablen = 0 # 词典词长 self.testset = 0 # 测试集
2.导入和训练数据集,生成算法必须的参数和数据结构:
def train_set(self,trainset,classVec): self.cate_prob(classVec) # 计算每个分类在数据集中的概率:P(yi)
self.doclength = len(trainset) tempset = set() [tempset.add(word) for doc in trainset for word in doc ] # Th成词典 self.vocabulary= list(tempset) self.vocablen = len(self.vocabulary) self.calc_wordfreq(trainset) # 计算词频数据集 self.build_tdm() # 按分类累计向量空间的每维值:P(x|yi)
3.cate_prob 函数:计算在数据集中每个分类的概率:P(yi)
def cate_prob(self,classVec): self.labels = classVec labeltemps = set(self.labels) # 获取全部分类 for labeltemp in labeltemps: # 统计列表中重复的分类:self.labels.count(labeltemp) self.Pcates[labeltemp] = float(self.labels.count(labeltemp))/float(len(self.labels))
4.calc_wordfreq 函数:生成普通的词频向量
# Th成普通的词频向量 def calc_wordfreq(self,trainset): self.idf = np.zeros([1,self.vocablen]) # 1*词典数 self.tf = np.zeros([self.doclength,self.vocablen]) # 训练集文件数*词典数 for indx in xrange(self.doclength): # 遍历所有的文本 for word in trainset[indx]: # 遍历文本中的每个词 self.tf[indx,self.vocabulary.index(word)] +=1 # 找到文本的词在字典中的位置+1 for signleword in set(trainset[indx]): self.idf[0,self.vocabulary.index(signleword)] +=1
5.build_tdm 函数:按分类累计计算向量空间的每维值:P(x|yi)
#按分类累计向量空间的每维值:P(x|yi) def build_tdm(self): self.tdm = np.zeros([len(self.Pcates),self.vocablen]) # 类别行*词典列 sumlist = np.zeros([len(self.Pcates),1]) # 统计每个分类的总值 for indx in xrange(self.doclength): self.tdm[self.labels[indx]] += self.tf[indx] # 将同一类别的词向量空间值加总 # 统计每个分类的总值--是个标量 sumlist[self.labels[indx]]= np.sum(self.tdm[self.labels[indx]]) self.tdm = self.tdm/sumlist # Th成 P(x|yi)
6.map2vocab
函数:将测试集映射到当前词典
def map2vocab(self,testdata): self.testset = np.zeros([1,self.vocablen]) for word in testdata: self.testset[0,self.vocabulary.index(word)] +=1
7.predict 函数:预测分类结果,输出预测的分类类别
def predict(self,testset): if np.shape(testset)[1] != self.vocablen: # 如果测试集长度与词典不相等,退出程序 print "输入错误"
exit(0) predvalue = 0 # 初始化类别概率 predclass = "" # 初始化类别名称 for tdm_vect,keyclass in zip(self.tdm,self.Pcates): # P(x|yi) P(yi) temp = np.sum(testset*tdm_vect*self.Pcates[keyclass]) # 变量 tdm,计算最大分类值 if temp > predvalue:
predvalue = temp predclass = keyclass return predclass
三. 算法改进
为普通的词频向量使用 TF-IDF 策略,使之有能力修正多种偏差。
4.calc_tfidf 函数:以 tf-idf 方式Th成向量空间:
# Th成 tf-idf def calc_tfidf(self,trainset): self.idf = np.zeros([1,self.vocablen]) self.tf = np.zeros([self.doclength,self.vocablen])
for indx in xrange(self.doclength): for word in trainset[indx]: self.tf[indx,self.vocabulary.index(word)] +=1 # 消除不同句长导致的偏差 self.tf[indx] = self.tf[indx]/float(len(trainset[indx]))
for signleword in set(trainset[indx]): self.idf[0,self.vocabulary.index(signleword)] +=1 self.idf = np.log(float(self.doclength)/self.idf) self.tf = np.multiply(self.tf,self.idf) # 矩阵与向量的点乘 tf x idf
四. 评估分类结果
# -*- coding: utf-8 -*- import sys import os from numpy import * import numpyas np from Nbayes_lib import * dataSet,listClasses = loadDataSet() # 导入外部数据集 # dataset: 句子的词向量, # listClass 是句子所属的类别 [0,1,0,1,0,1] nb = NBayes() # 实例化 nb.train_set(dataSet,listClasses) # 训练数据集 nb.map2vocab(dataSet[0]) # 随机选择一个测试句 print nb.predict(nb.testset) # 输出分类结果
分类结果
1
执行我们创建的朴素贝叶斯类,获取执行结果
标签:tf-idf 最大 贝叶斯 向量 float 推导 sha 构造方法 概率
原文地址:http://www.cnblogs.com/taich-flute/p/6813815.html