排序——堆排序算法

标签：步骤   1.5   算法   建立   [1]   结果   cout   比较   http   

堆排序利用的完全二叉树这种数据结构所设计的一种算法，不过也是选择排序的一种。

堆实质上是满足如下性质的完全二叉树：k[i]<=k[2*i]&&k[i]<=k[2*i+1]或者k[i]>=k[2*i]&&k[i]>=k[2*i+1]，

树中任一非叶子结点的关键字均不大于（或不小于）其左右孩子（若存在）结点的关键字。

堆分大顶堆和小顶堆：k[i]<=k[2*i]&&k[i]<=k[2*i+1]是小顶堆，k[i]>=k[2*i]&&k[i]>=k[2*i+1]是大顶堆。堆排序利用了大顶堆（或小顶堆）堆顶记录的关键字最大（或最小）这一特征，使得在当前无序区中选取最大（或最小）关键字的记录变得简单。

堆排序的实现：首先，初始化堆，是对所有的非叶子结点进行筛选。最后一个非叶子节点元素的下标是[n/2]向下取最大值，所以筛选只需要从第[n/2]向下取整个元素开始，从后往前进行调整。然后从最后一个非叶子节点开始，每次都是从父节点、左孩子、右孩子中进行比较交换，交换可能会引起孩子节点不满足堆的性质，所以每次交换之后需要重新对被交换的孩子将节点进行调整。有了初始堆之后就可以进行排序了。

　　堆排序是一种选择排序。建立的初始堆为初始的无序区。

　　排序开始，首先输出堆顶元素（因为它是最值），将堆顶元素和最后一个元素交换，这样，第n个位置（即最后一个位置）作为有序区，前n-1个位置仍是无序区，对无序区进行调整，得到堆之后，再交换堆顶和最后一个元素，这样有序区长度变为2。

　　不断进行此操作，将剩下的元素重新调整为堆，然后输出堆顶元素到有序区。每次交换都导致无序区-1，有序区+1。不断重复此过程直到有序区长度增长为n-1，排序完成。

举例：一个10位数的数列[5 4 3 1 2 9 7 8 0 6]

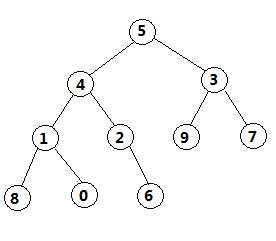
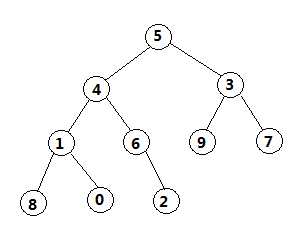
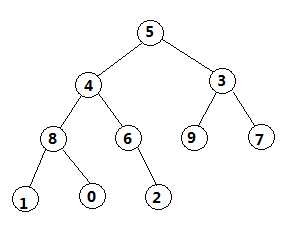
按照这样步骤，循环往复，即每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质，因此每次交换之后要重新对被交换的孩子节点进行调整)。有了初始堆之后就可以进行排序了。

从上述过程可知，堆排序其实也是一种选择排序，是一种树形选择排序。只不过直接选择排序中，为了从R[1...n]中选择最大记录，需比较n-1次，然后从R[1...n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过，而树形选择排序恰好利用树形的特点保存了部分前面的比较结果，因此可以减少比较次数。对于n个关键字序列，最坏情况下每个节点需比较log2(n)次，因此其最坏情况下时间复杂度为nlogn。堆排序为不稳定排序，不适合记录较少的排序。

代码（C语言）：

void HeapAdjust(int *a,int i,int size)
{
    int lchild=2*i;       
    int rchild=2*i+1;     
    int max=i;            
    if(i<=size/2)         
    {
        if(lchild<=size&&a[lchild]>a[max])
        {
            max=lchild;
        }
        if(rchild<=size&&a[rchild]>a[max])
        {
            max=rchild;
        }
        if(max!=i)
        {
            swap(a[i],a[max]);
            HeapAdjust(a,max,size);
        }
    }
}
void HeapSort(int *a,int size)  
{
    int i;
    for(i=size/2; i>=1; i--){
        HeapAdjust(a,i,size);
    }
    for(i=size;i>=1;i--)
    {
        //cout<<a[1]<<" ";
        swap(a[1],a[i]);           
          //BuildHeap(a,i-1);      
          HeapAdjust(a,1,i-1);     
    }
}

排序——堆排序算法

标签：步骤   1.5   算法   建立   [1]   结果   cout   比较   http   

原文地址：http://www.cnblogs.com/hey-man/p/6847591.html