标签：img 二分 节点 [] 灵活 const 3.1 let 分析方法
这里我借用百度百科上的解释：斐波那契数，亦称之为斐波那契数列（意大利语： Successione di Fibonacci)，又称黄金分割数列、费波那西数列、费波拿契数、费氏数列，指的是这样一个数列：0、1、1、2、3、5、8、13、21、……在数学上，斐波纳契数列以如下被以递归的方法定义：F0=0，F1=1，Fn=Fn-1+Fn-2（n>=2，n∈N*），用文字来说，就是斐波那契数列列由 0 和 1 开始，之后的斐波那契数列系数就由之前的两数相加。特别指出：0不是第一项，而是第零项。
求第N个斐波那契数比较简单可以直接套用公式n = 1,2 时，fib(n) = 1；n > 2 时，fib(n) = fib(n-2) + fib(n-1)在计算时有两种算法：递归和非递归。如下：
1 //非递归算法 2 long long fib1(size_t N) { 3 long long a = 0, b = 1, c = 0; 4 if (N < 2) { 5 return N; 6 } 7 else { 8 for (long long i = 2; i <= N; ++i) { 9 c = a + b; 10 a = b; 11 b = c; 12 } 13 } 14 return c; 15 } 16 int main() 17 { 18 printf("%lld", fib1(10)); 19 getchar(); 20 return 0; 21 } //此算法最大的优点是不存在重复计算，故效率比递归算法快的多得多。
1 //递归算法 2 long long fib2(size_t N) { 3 if (N < 2) 4 return N; 5 return fib2(N - 1) + fib2(N - 2); 6 } 7 int main() 8 { 9 printf("%lld", fib2(10)); 10 getchar(); 11 return 0; 12 }
递归可以使程序看起来比较简洁，但缺点是效率比较低，并且可能导致栈溢出，当需要计算的数稍大一点，就需要很长的计算时间，因此需要灵活使用递归。
1 template<typename T> 2 T* BinarySearch(T* array,int number,const T& data) 3 { 4 assert(number>=0); 5 int left = 0; 6 int right = number-1; 7 while (right >= left) 8 { 9 int mid = (left&right) + ((left^right)>>1); 10 if (array[mid] > data) 11 { 12 right = mid - 1; 13 } 14 else if (array[mid] < data) 15 { 16 left = mid + 1; 17 } 18 else 19 { 20 return (array + mid); 21 } 22 } 23 return NULL; 24 }
1 template<typename T> 2 T* BinarySearch(T* left,T* right,const T& data) 3 { 4 assert(left); 5 assert(right); 6 if (right >=left) 7 { 8 T* mid =left+(right-left)/2; 9 if (*mid == data) 10 return mid; 11 else 12 return *mid > data ? BinarySearch(left, mid - 1, data) : BinarySearch(mid + 1, right, data); 13 } 14 else 15 { 16 return NULL; 17 } 18 }
使用非递归算法求到第n个斐波那契数，是从第2个数开始，将前两个数相加求求后一个数，再将后一个数赋值给前一个数，再计算前两个数相加的结果。依次类推直到第n个数，用n-1个数和n-2个数相加求出结果，这样的好处是，我们只计算了n-1次就求出了结果，即时间复杂度为O(n)；我们以代码中测试数10为例详解求第十个数的过程。当N=10时，进入函数首先判断，然后走下面的分支开始计算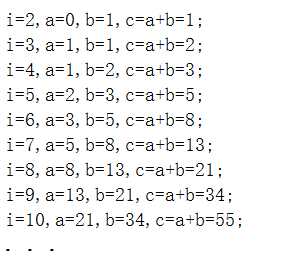
计算了N-1次，得出了结果所以时间复杂度是O（N）。
非递归算法空间复杂度分析
此函数内部最多时一共开辟了a, b, c, i四个变量空间复杂度是常数，即为O（1）。
在递归算法中，求解fib2(n)，把它推到求解fib2(n-1)和fib2(n-2)。也就是说，为计算fib2(n)，必须先计算
fib2(n-1)和fib2(n-2)，而计算fib2(n-1)和fib2(n-2)，时按照表达式及计算法则，需先计算又必须先计算fib2(n-1)，而fib2(n-1)由fib2(n-2)和fib2(n-3)计算得来，而这之中的和fib2(n-2)由fib2(n-3)和fib2(n-4)计算得来......依次类推，表面上看不出有何复杂度，但是仔细分析可知，每一个计算fib2(n)的分支都会衍生出计算直至(1)和fib(0)，也就是说每个分支都要自己计算数本身到1的斐波那契数列，这样就增加了庞大且冗杂的运算量，还是以10 为例详细计算说明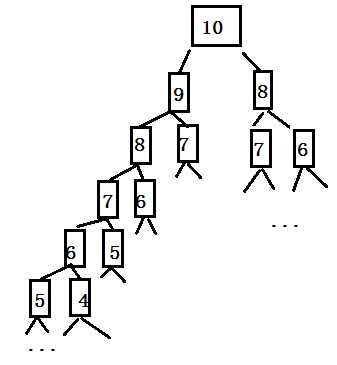
图中数字代表第N个斐波那契数，图中没有全部将计算步骤画出来，但是已经足够说明问题，它的每一步计算都被分成计算前两个斐波那契数，以此类推。那么这就形成了一颗二叉树，虽然不是满二叉树，但是我们分析的是最坏时间复杂度，而且只要估算出来递归次数随N增长的趋势即可，故可以近似将它看成满二叉树，其中的节点数就是计算的次数，也就是复杂度，由公式：节点数=2^h-1（h为树的高度）可得O（2^n）。
递归算法空间复杂度分析：
递归最深的那一次所耗费的空间足以容纳它所有递归过程。递归产生的栈侦是要销毁的，所以空间也就释放了，要返回上一层栈侦继续计算+号后面的数，所以它所需要的空间不是一直累加起来的，之后产生的栈侦空间都小于递归最深的那一次所耗费的空间。
递归的深度*每次递归所需的辅助空间的个数 ，所以空间复杂度是：O(N)
1 class Temp 2 { 3 public: 4 Temp(){ 5 ++N; 6 Sum += N; 7 } 8 static void Reset(){ 9 N = 0; 10 Sum = 0; 11 } 12 static int GetSum(){ 13 return Sum; 14 } 15 private: 16 static int N; 17 static int Sum; 18 }; 19 int Temp::N = 0; 20 int Temp::Sum = 0; 21 int solution_Sum(int n){ 22 Temp::Reset(); 23 Temp *a = new Temp[n]; 24 delete[]a; 25 a = 0; 26 return Temp::GetSum(); 27 } 28 int main(){ 29 cout << solution_Sum(100) << endl; 30 getchar(); 31 return 0; 32 33 }
标签：img 二分 节点 [] 灵活 const 3.1 let 分析方法
原文地址：http://www.cnblogs.com/33debug/p/6848330.html
