标签:pre ges 类方法 工具 jpg 技术分享 调用 abs for
1.K-均值聚类法的概述
% 利用K-均值聚类的原理,实现对一组数据的分类。这里以一组二维的点为例。
N = 40; % 点的个数
X = 10*rand(1,N);
Y = 10*rand(1,N); % 随机生成一组横纵坐标取值均在(0,10)之间的点,X Y 分别代表横纵坐标
plot(X, Y, ‘r*‘); % 绘出原始的数据点
xlabel(‘X‘);
ylabel(‘Y‘);
title(‘聚类之前的数据点‘);
n = 2; %将所有的数据点分为两类
m = 1; %迭代次数
eps = 1e-7; % 迭代结束的阈值
u1 = [X(1),Y(1)]; %初始化第一个聚类中心
u2 = [X(2),Y(2)]; %初始化第二个聚类中心
U1 = zeros(2,100);
U2 = zeros(2,100); %U1,U2 用于存放各次迭代两个聚类中心的横纵坐标
U1(:,2) = u1;
U2(:,2) = u2;
D = zeros(2,N); %初始化数据点与聚类中心的距离
while(abs(U1(1,m) - U1(1,m+1)) > eps || abs(U1(2,m) - U1(2,m+1) > eps || abs(U2(1,m) - U2(1,m+1)) > eps || abs(U2(2,m) - U2(2,m+1)) > eps))
m = m +1;
% 计算所有点到两个聚类中心的距离
for i = 1 : N
D(1,i) = sqrt((X(i) - U1(1,m))^2 + (Y(i) - U1(2,m))^2);
end
for i = 1 : N
D(2,i) = sqrt((X(i) - U2(1,m))^2 + (Y(i) - U2(2,m))^2);
end
A = zeros(2,N); % A用于存放第一类的数据点
B = zeros(2,N); % B用于存放第二类的数据点
for k = 1: N
[MIN,index] = min(D(:,k));
if index == 1 % 点属于第一个聚类中心
A(1,k) = X(k);
A(2,k) = Y(k);
else % 点属于第二个聚类中心
B(1,k) = X(k);
B(2,k) = Y(k);
end
end
indexA = find(A(1,:) ~= 0); % 找出第一类中的点
indexB = find(B(1,:) ~= 0); % 找出第二类中的点
U1(1,m+1) = mean(A(1,indexA));
U1(2,m+1) = mean(A(2,indexA));
U2(1,m+1) = mean(B(1,indexB));
U2(2,m+1) = mean(B(2,indexB)); % 更新两个聚类中心
end
figure;
plot(A(1,indexA) , A(2,indexA), ‘*b‘); % 作出第一类点的图形
hold on
plot(B(1,indexB) , B(2,indexB), ‘oy‘); %作出第二类点的图形
hold on
centerx = [U1(1,m) U2(1,m)];
centery = [U1(2,m) U2(2,m)];
plot(centerx , centery, ‘+g‘); % 画出两个聚类中心点
xlabel(‘X‘);
ylabel(‘Y‘);
title(‘聚类之后的数据点‘);
disp([‘迭代的次数为:‘,num2str(m)]);
得到的分类结果如下:
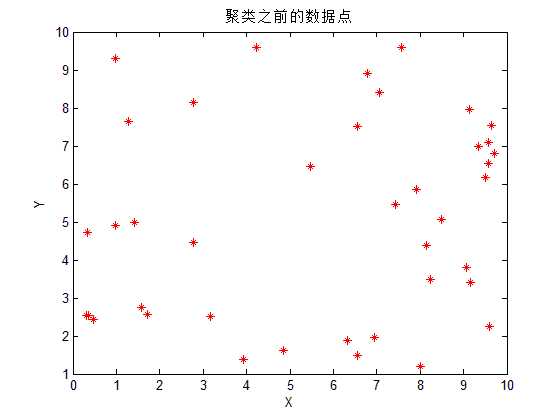
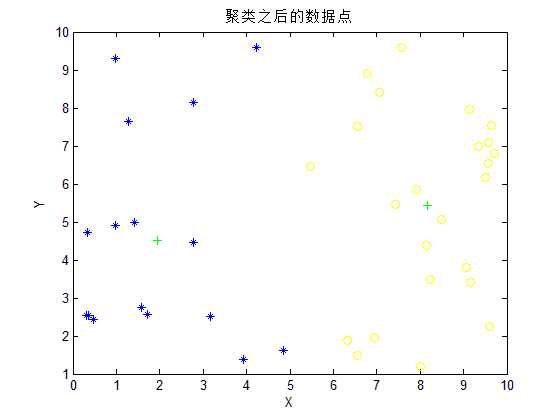
50个随机生成的点分为两类迭代只需要4步,从上图来看,分类的效果还是不错的。但是每次运行可能分类的结果会不一样,这是因为这些点是随机生成的,而且也没有明确的分类标准的缘故。
标签:pre ges 类方法 工具 jpg 技术分享 调用 abs for
原文地址:http://www.cnblogs.com/yezuhui/p/6853269.html