标签:std 大量 规模 计算 平衡 分享 print 比较 重要
上一回说了基本粒子群算法的实现,并且给出了C语言代码。这一篇主要讲解影响粒子群算法的一个重要参数---w。我们已经说过粒子群算法的核心的两个公式为:
Vid(k+1)=w*Vid(k)+c1*r1*(Pid(k)-Xid(k))+c2*r2*(Pgd(k)-Xid(k))
Xid(k+1) = Xid(k) + Vid(k+1)
标红的w即是本次我们要讨论的参数。之前w是不变的(默认取1),而现在w是变化的,w称之为惯性权重,体现的是粒子继承先前速度的能力。 经验表明:一个较大的惯性权重有利于全局搜索,而一个较小的惯性权重则更有利于局部搜索。为了更好地平衡算法的全局搜索能力与局部搜索能力,Shi.Y提出了线性递减惯性权重(LDIW)
即:w(k) = w_end + (w_start- w_end)*(Tmax-k)/Tmax。其中w_start 为初始惯性权重,w_end 为迭代至最大次数时的惯性权重;k为当前迭代次数, Tmax为最大迭代次数。一般来说,w_start=0.9,w_end=0.4时,算法的性能最好。这样随着迭代的进行,惯性权重从0.9递减到0.4,迭代初期较大的惯性权重使算法保持了较强的全局搜索能力。而迭代后期较小的惯性权重有利于算法进行更精确的局部搜索。线性惯性权重,只是一种经验做法,常用的惯性权重还包括 以下几种。
(3) w(k) = w_start - (w_start-w_end)*(k/Tmax)^2
(4) w(k) = w_start + (w_start-w_end)*(2*k/Tmax - (k/Tmax)^2)
(5) w(k) = w_end*(w_start/w_end)^(1/(1+c*k/Tmax)) ,c为常数,比如取10等。
本例的目的就是比较这5种不同的w取值,对于PSO寻优的影响。比较的方法为每种w取值,重复实验若干次(比如100次),比较平均最优解的大小,陷入次优解的次数,以及接近最优解的次数。 这样对于5种方法的优劣可以有一个直观的比较。
代码如下:
/*
* 使用C语言实现粒子群算法(PSO) 改进版本
* 参考自《MATLAB智能算法30个案例分析》
* update: 16/12/3
* 主要改进的方面体现在w的选择上面
* 本例的寻优非线性函数为
* f(x,y) = sin(sqrt(x^2+y^2))/(sqrt(x^2+y^2)) + exp((cos(2*PI*x)+cos(2*PI*y))/2) - 2.71289
* 该函数有很多局部极大值点,而极限位置为(0,0),在(0,0)附近取得极大值
*/
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<time.h>
#define c1 1.49445 //加速度因子一般是根据大量实验所得
#define c2 1.49445
#define maxgen 300 // 迭代次数
#define repeat 100 // 重复实验次数
#define sizepop 20 // 种群规模
#define popmax 2 // 个体最大取值
#define popmin -2 // 个体最小取值
#define Vmax 0.5 // 速度最大值
#define Vmin -0.5 //速度最小值
#define dim 2 // 粒子的维数
#define w_start 0.9
#define w_end 0.4
#define PI 3.1415926 //圆周率
double pop[sizepop][dim]; // 定义种群数组
double V[sizepop][dim]; // 定义种群速度数组
double fitness[sizepop]; // 定义种群的适应度数组
double result[maxgen]; //定义存放每次迭代种群最优值的数组
double pbest[sizepop][dim]; // 个体极值的位置
double gbest[dim]; //群体极值的位置
double fitnesspbest[sizepop]; //个体极值适应度的值
double fitnessgbest; // 群体极值适应度值
double genbest[maxgen][dim]; //每一代最优值取值粒子
//适应度函数
double func(double * arr)
{
double x = *arr; //x 的值
double y = *(arr+1); //y的值
double fitness = sin(sqrt(x*x+y*y))/(sqrt(x*x+y*y)) + exp((cos(2*PI*x)+cos(2*PI*y))/2) - 2.71289;
return fitness;
}
// 种群初始化
void pop_init(void)
{
for(int i=0;i<sizepop;i++)
{
for(int j=0;j<dim;j++)
{
pop[i][j] = (((double)rand())/RAND_MAX-0.5)*4; //-2到2之间的随机数
V[i][j] = ((double)rand())/RAND_MAX-0.5; //-0.5到0.5之间
}
fitness[i] = func(pop[i]); //计算适应度函数值
}
}
// max()函数定义
double * max(double * fit,int size)
{
int index = 0; // 初始化序号
double max = *fit; // 初始化最大值为数组第一个元素
static double best_fit_index[2];
for(int i=1;i<size;i++)
{
if(*(fit+i) > max)
max = *(fit+i);
index = i;
}
best_fit_index[0] = index;
best_fit_index[1] = max;
return best_fit_index;
}
// 迭代寻优,传入的参数为一个整数,取值为1到5,分别代表5种不同的计算w的方法
void PSO_func(int n)
{
pop_init();
double * best_fit_index; // 用于存放群体极值和其位置(序号)
best_fit_index = max(fitness,sizepop); //求群体极值
int index = (int)(*best_fit_index);
// 群体极值位置
for(int i=0;i<dim;i++)
{
gbest[i] = pop[index][i];
}
// 个体极值位置
for(int i=0;i<sizepop;i++)
{
for(int j=0;j<dim;j++)
{
pbest[i][j] = pop[i][j];
}
}
// 个体极值适应度值
for(int i=0;i<sizepop;i++)
{
fitnesspbest[i] = fitness[i];
}
//群体极值适应度值
double bestfitness = *(best_fit_index+1);
fitnessgbest = bestfitness;
//迭代寻优
for(int i=0;i<maxgen;i++)
{
for(int j=0;j<sizepop;j++)
{
//速度更新及粒子更新
for(int k=0;k<dim;k++)
{
// 速度更新
double rand1 = (double)rand()/RAND_MAX; //0到1之间的随机数
double rand2 = (double)rand()/RAND_MAX;
double w;
double Tmax = (double)maxgen;
switch(n)
{
case 1:
w = 1;
case 2:
w = w_end + (w_start - w_end)*(Tmax-i)/Tmax;
case 3:
w = w_start -(w_start-w_end)*(i/Tmax)*(i/Tmax);
case 4:
w = w_start + (w_start-w_end)*(2*i/Tmax-(i/Tmax)*(i/Tmax));
case 5:
w = w_end*(pow((w_start/w_end),(1/(1+10*i/Tmax))));
default:
w = 1;
}
V[j][k] = w*V[j][k] + c1*rand1*(pbest[j][k]-pop[j][k]) + c2*rand2*(gbest[k]-pop[j][k]);
if(V[j][k] > Vmax)
V[j][k] = Vmax;
if(V[j][k] < Vmin)
V[j][k] = Vmin;
// 粒子更新
pop[j][k] = pop[j][k] + V[j][k];
if(pop[j][k] > popmax)
pop[j][k] = popmax;
if(pop[j][k] < popmin)
pop[j][k] = popmin;
}
fitness[j] = func(pop[j]); //新粒子的适应度值
}
for(int j=0;j<sizepop;j++)
{
// 个体极值更新
if(fitness[j] > fitnesspbest[j])
{
for(int k=0;k<dim;k++)
{
pbest[j][k] = pop[j][k];
}
fitnesspbest[j] = fitness[j];
}
// 群体极值更新
if(fitness[j] > fitnessgbest)
{
for(int k=0;k<dim;k++)
gbest[k] = pop[j][k];
fitnessgbest = fitness[j];
}
}
for(int k=0;k<dim;k++)
{
genbest[i][k] = gbest[k]; // 每一代最优值取值粒子位置记录
}
result[i] = fitnessgbest; // 每代的最优值记录到数组
}
}
// 主函数
int main(void)
{
clock_t start,finish; //程序开始和结束时间
start = clock(); //开始计时
srand((unsigned)time(NULL)); // 初始化随机数种子
for(int i=1;i<=5;i++)
{
int near_best = 0; // 接近最优解的次数
double best_sum = 0; // 重复最优值求和
double best = 0; // 重复实验得到的最优解
for(int j=0;j<repeat;j++)
{
PSO_func(i); // 第i种w参数取值
double * best_fit_index = max(result,maxgen);
double best_result = *(best_fit_index+1); //最优解
if(best_result > 0.95)
near_best++;
if(best_result>best)
best = best_result;
best_sum += best_result;
}
double average_best = best_sum/repeat; //重复实验平均最优值
printf("w参数的第%d种方法:\n",i);
printf("重复实验%d次,每次实验迭代%d次,接近最优解的实验次数为%d次,求得最优值为:%lf,平均最优值为:%lf\n",repeat,maxgen,near_best,best,average_best);
}
finish = clock(); //结束时间
double duration = (double)(finish - start)/CLOCKS_PER_SEC; // 程序运行时间
printf("程序运行耗时:%lf\n",duration);
return 0;
}
程序运行结果如下:
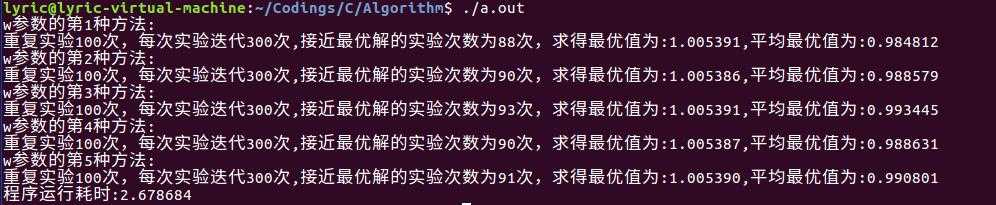
从实验的结果来看,第3种w的取法,无论是接近最优解的的次数,最优值大小,还是平均最优值,都是5种里面最好的。其原因解释如下:通过w的表达式可以看出,前期w变化较慢,取值较大,维持了算法的全局搜索能力;后期w变化变化较快,极大地提高了算法的局部搜索能力寻优能力,从而取得了很好的求解效果。
从总体上来看,在大部分的情况下,无论w是5种里面哪种取法,得到的结果都很好地接近实际的最优解,这说明了粒子群算法的搜索寻优能力还是很强的。
标签:std 大量 规模 计算 平衡 分享 print 比较 重要
原文地址:http://www.cnblogs.com/yezuhui/p/6853263.html