标签:for 数组 nbsp image delete offer 空间复杂度 itblog 取出
今天做剑指offer上的一道求逆序对的题,用到了归并排序的思想,时间复杂度为O(nlogn),空间复杂度为O(n)。
偷了个懒从网上找到别人总结的归并排序的算法思想和code,直接粘过来方便随时查。
原文:http://www.cnblogs.com/jianboqi/archive/2013/01/15/2860500.html
之前看了选择和插入排序,这两个算法是的时间复杂度均为O(n^2),而随着问题规模n的增大,插入和选择排序都比较慢。
归并排序时的时间复杂度为O(nlgn) 其主要思想是分治法(divide and conquer),分就是要将n个元素的序列划分为两个序列,再将两个序列划分为4个序列,
直到每个序列只有一个元素,最后,再将两个有序序列归并成一个有序的序列。
例如两个序列:

要归并成一个有序的序列,按照我们常规的方法,我们每次从两个列表开头元素选取较小的一个,直到某一个列表到达底部,再将另一个剩下部分顺序取出。其实如果将每个元素最后添加一个最大值,则无需判断是否达到列表尽头。

代码如下:merge函数的功能为将A中[low,mid],[mid+1,high]归并成一个有序的片段。
template<class T> void merge(T A[],int low,int mid,int high)
{
//low to mid as the left array mid+1 to high as the right array
int llen = mid-low+2;
int rlen = high-mid+1;
T *left = (T*)new T[llen];
T *right = (T*)new T[rlen];
//copy the low to mid to the temp array left
for (int i=0;i<llen-1;i++)
{
left[i] = A[low+i];
}
for (i=0;i<rlen-1;i++)
{
right[i] = A[mid+1+i];
}
//set the sentinel
left[llen-1] = numeric_limits<T>::max();
right[rlen-1]= numeric_limits<T>::max();
//merge the two array and copy to A[low,high];
int j = 0;
int k = 0;
for (i = low; i < high+1 ;i++)
{
if (left[j] < right[k])
{
A[i] = left[j];
j++;
}
else
{
A[i] = right[k];
k++;
}
}
delete [] left;
delete [] right;
}
归并排序就是多次调用merge
template<class T> merge_sort(T A[],int low,int high)
{
int mid = (low+high)/2;
if (low < high)
{
merge_sort(A,low,mid);
merge_sort(A,mid+1,high);
merge(A,low,mid,high);
}
}
这是一个递归算法,这个算法的理解其实可以借助下面这个图:
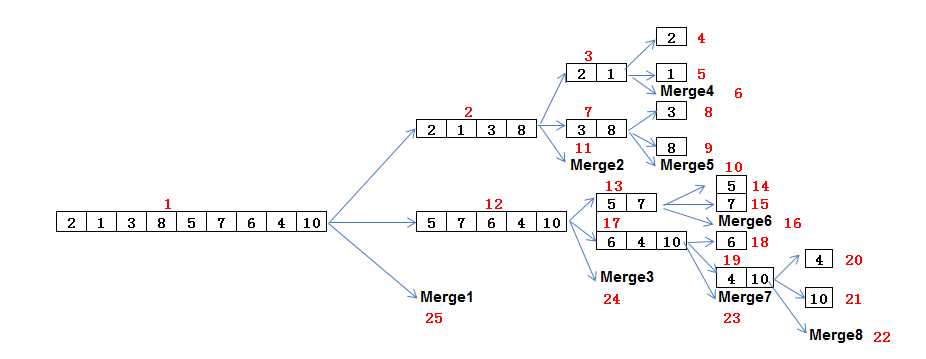
对于原始的数组2,1,3,8,5,7,6,4,10,在整个过程执行的是顺序是途中红色编号1-20。虽然我们描述中说的是程序先分解,再归并,但实际过程是一边分解一边归并,前半部分分先排好序,后半部分再拍好,最后整个归并为一个完整的序列,途中的merge过程它所在层的两个序列的merge过程:下图展示了每个merge过程对作用于数组的哪部分(红色)。
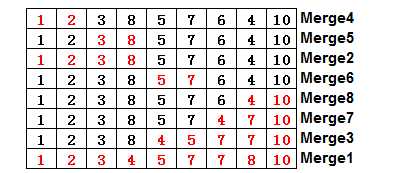
整个过程就像一个动态的树,执行顺序就是对树的先序遍历顺序。
标签:for 数组 nbsp image delete offer 空间复杂度 itblog 取出
原文地址:http://www.cnblogs.com/Bill-LHR/p/6868746.html