标签:off ... http 随机 median while int iostream return
快速排序—分而治之
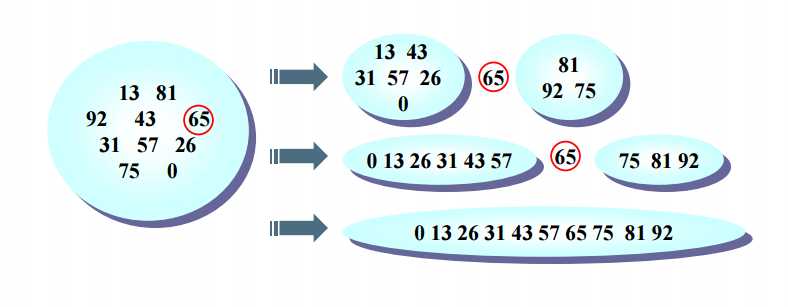
最好情况:每次正好等分 T(N) = O(logN)
选主元:
1.令pivot = A[0] 1 2 3 4 5 ...N-1 N 的话T(N) = O(N^2)
2.随机函数取 要花时间
3.常用 取头中尾的中位数 8 12 3 取8
ElementType Median3(ElementType A[], int Left, int Right) { int Center = (Left + Right) / 2; if (A[Left] > A[Center]) Swap(&A[Left], &A[Center]); if (A[Left] > A[Right]) Swap(&A[Left], &A[Right]); if (A[Center] > A[Right]) Swap(&A[Center], &A[Right]); //此时A[Left] <= A[Center] <= A[Right] Swap(&A[Center], &A[Right-1]); //将基准Pivot藏到右边 //只需考虑A[Left+1]...A[Right-2]; return A[Right - 1]; }
子集划分:
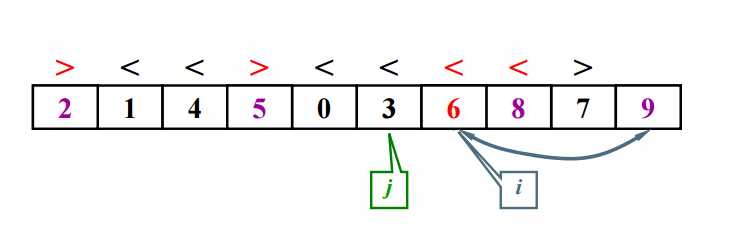
快排快的一个重要原因:主元被选中后 并在子集划分完成后 被一次放到正确的位置
如果有元素正好等于Pivot
停下来交换 主元会被换到中间的位置 基本等分 √
不理它 继续移动指针 主元可能会被放在端点
void Qsort(ElementType A[], int Left, int Right) { int Pivot, Low, High; if (Cutoff <= Right - Left) { Pivot = Median3(A, Left, Right); Low = Left; High = Right-1; while (1) { while (A[++Low] < Pivot); while (A[--High] > Pivot); if (Low < High) Swap(&A[Low], &A[High]); else break; } Swap(&A[Low], &A[Right-1]); Qsort(A, Left, Low-1); Qsort(A, Low+1, Right); } else InsertionSort(A+Left, Right-Left+1); //元素太少,用简单排序 }
问题:
用递归 占用堆栈空间且费时间
对小规模的数据(例如N不到100)可能不如插入排序快
解决:当递归的数据规模充分小时停止递归 直接调用简单排序(如插入排序)
Cutoff为阈值
代码:

#include <iostream> using namespace std; typedef long long ElementType; #define Cutoff 50 void Swap(ElementType *a, ElementType *b) { ElementType t = *a; *a = *b; *b = t; } void InsertionSort(ElementType A[], int N) { int P, i; ElementType Tmp; for (P = 1; P < N; P++) { Tmp = A[P]; for (i = P; i > 0 && A[i-1] > Tmp; i--) A[i] = A[i-1]; A[i] = Tmp; } } ElementType Median3(ElementType A[], int Left, int Right) { int Center = (Left + Right) / 2; if (A[Left] > A[Center]) Swap(&A[Left], &A[Center]); if (A[Left] > A[Right]) Swap(&A[Left], &A[Right]); if (A[Center] > A[Right]) Swap(&A[Center], &A[Right]); //此时A[Left] <= A[Center] <= A[Right] Swap(&A[Center], &A[Right-1]); //将基准Pivot藏到右边 //只需考虑A[Left+1]...A[Right-2]; return A[Right - 1]; } void Qsort(ElementType A[], int Left, int Right) { int Pivot, Low, High; if (Cutoff <= Right - Left) { Pivot = Median3(A, Left, Right); Low = Left; High = Right-1; while (1) { while (A[++Low] < Pivot); while (A[--High] > Pivot); if (Low < High) Swap(&A[Low], &A[High]); else break; } Swap(&A[Low], &A[Right-1]); Qsort(A, Left, Low-1); Qsort(A, Low+1, Right); } else InsertionSort(A+Left, Right-Left+1); //元素太少,用简单排序 } void QuickSort(ElementType A[], int N) { Qsort(A, 0, N-1); } int main() { int N, i; ElementType A[110000]; cin >> N; for (i = 0; i < N; i++) cin >> A[i]; QuickSort(A, N); for (i = 0; i < N-1; i++) cout << A[i] << " "; cout << A[i]; return 0; }
PTA运行结果:
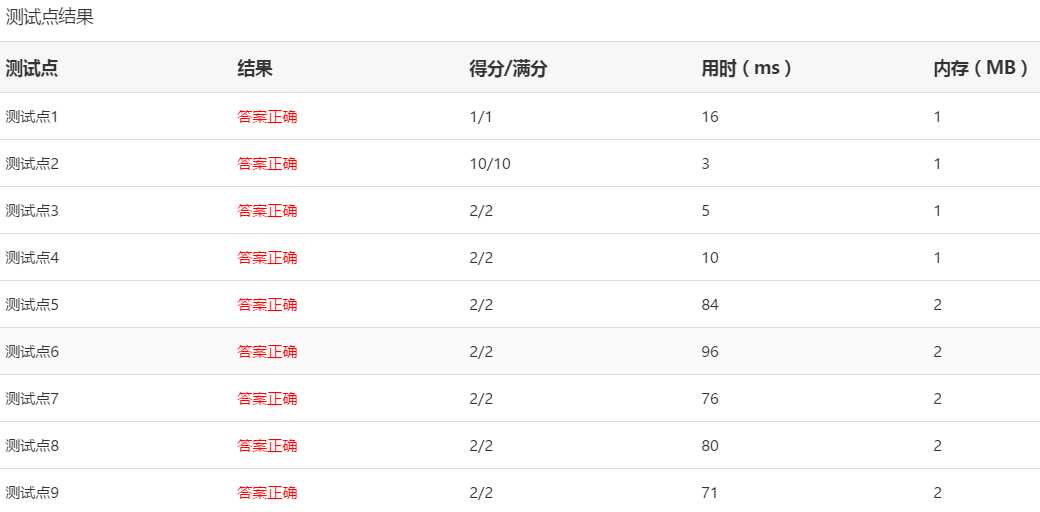
标签:off ... http 随机 median while int iostream return
原文地址:http://www.cnblogs.com/whileskies/p/6876020.html