标签:res 6.4 tom rar 序列 分享 type ide 描述
本博客的代码的思想和图片参考:好大学慕课浙江大学陈越老师、何钦铭老师的《数据结构》
排序
1.函数的名称规范
void X_Sort ( ElementType A[], int N )
2.大多数情况下,为简单起见,讨论从小大的整数排序
3.N是正整数
4只讨论基于比较的排序( >= < 有定义 )
5.只讨论内部排序
6稳定性:任意两个相等的数据,排序前后的相对位置不发生改变
7.没有一种排序是任何情况下都表现最好的
第一趟:比较第一个元素和第二元素,如果第一个元素比第二个元素大,就交换位置,否则就不交换位置;在比较第二元素和第三个元素的大小,如果第二个元素比第三个元素大,交换位置,否则不交换位置;然后接着比较第三个元素和第四个元素…… 直到比较到第N-1个元素和第N个元素。这样一趟下来,可以确定最大的元素在N位置
第二趟:比较第一个元素和第二元素,如果第一个元素比第二个元素大,就交换位置,否则就不交换位置;在比较第二元素和第三个元素的大小,如果第二个元素比第三个元素大,交换位置,否则不交换位置;然后接着比较第三个元素和第四个元素……,直到比较到N-2 和N-1个元素。这样,第二趟下面,第二大的元素可以确定在N-1位置。
第三趟……
…
这样到第N趟,就可以吧数组排序完成。
/*
* A method to implement bubble sort.If the bubble sort has no any swap
* operation at one time,indicating the array has been ordered.So we use a
* tag to make it effective
*@param a A integer array need to sort
*@param n The length of the array
*/
voidbubble_sort(elementType a[], int n) {
int i, j, flag;
for (i = n - 1; i >= 0; i--) {
flag = 0;
for (j = 0; j < i; j++) {
if (a[j] > a[j + 1]) {
swap(&a[j], &a[j + 1]);
flag = 1;
}
}
if (flag == 0) {
break;
}
}
}
最好的情况:如果这个数组本身就是有序的,那么时间复杂:T=O(N)
最坏的情况:如果这个数组本身就是逆序的,那么时间复杂度为T=O(N^2)
因为只有当前面的元素严格的大于后面元素时,才会交换位置,相对位置不会发生改变,那么该算法是稳定的。
选择排序的前提是保证数组中已有元素是有序的。例如在给数组的第i个元素排序(找合适位置)时,已经保证前面i-1个元素是有序的。
第一趟:当给数组中第一个元素排序时,因为就一个元素,默认就是有序的。
第二趟:当给数组中第二元素排序时,比较(前一个元素)第一个元素是否比他大,如果大,把前一个元素往后面摞一位,然后。
第三趟:给数组中第三个元素排序时,比较前一个元素是不是比他大,比他大,前一个元素向后摞一位。在比较在前面一个元素是否比他大,如果比他大,在吧在前一个元素往后摞一位;如果不比他大,那么刚才那个摞的那个空位就就放入该元素。
第四趟……
…
第N趟
/*
* Implemet insertion sort.
*@param a A integer array need to sort
*@param n The length of the array
*/
voidinsertion_sort(elementType a[], int n) {
int i, j;
elementType temp;
for (i = 1; i < n; i++) {
temp = a[i];
for (j = i; j > 0 && a[j - 1] > temp; j--) {
a[j] = a[j - 1];
}
a[j] = temp;
}
}
最好的情况:如果这个数组本身就是有序的,那么时间复杂:T=O(N)
最坏的情况:如果这个数组本身就是逆序的,那么时间复杂度为T=O(N^2)
因为只有当前面的元素严格的大于后面元素时,才会交换位置,相对位置不会发生改变,那么该算法是稳定的。
为了说明这个问题,我先给出一个例题:
给定初始序列{34, 8, 64, 51,32, 21},冒泡排序和插入排序分别需要多少次元素交换才能完成?
答:冒泡需要9次,选择排序也需要9次。这是一个巧合吗?
对于下标i<j,如果A[i]>A[j],则称(i,j)是一对逆序对(inversion)
问题:序列{34, 8, 64, 51, 32, 21}中有多少逆序对?
(34, 8) (34, 32) (34, 21) (64, 51) (64, 32) (64, 21) (51, 32) (51, 21) (32, 21)
有九个逆序对。
交换两个相邻的逆序对正好消去一个逆序对!
插入排序(冒泡排序)的时间复杂度可以重新定义为:
T(N,I)=O(N,I).I为N个元素中逆序对的个数
——如果需要排序的序列基本有序,则插入排序简单且高效
定理:任意N个不同元素组成的序列平均具有N ( N - 1 ) / 4 个逆序对。
定理:任何仅以交换相邻两元素来排序的算
法,其平均时间复杂度为 ( N^2 ) 。
这意味着:要提高算法效率,我们必须
1.每次消去不止1个逆序对!
2. 每次交换相隔较远的2个元素!
定义增量序列 D M > D M-1 > ... > D 1 = 1
对每个 D k 进行“D k -间隔”排序 ( k = M, M-1, ... 1 )
注意:“D k -间隔”有序的序列,在执行“D k-1 -间隔”排序后,仍然是“D k -
间隔”有序的。下面用一幅图片来说明希尔排序的过程
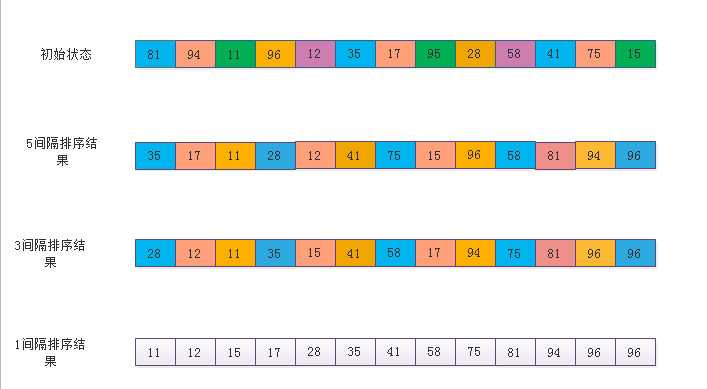
/*
* Implement base shell sort
*@param a A integer array need to sort
*@param n The length of the array
*/
voidshell_sort_base(elementType a[], int n) {
int i, j, d;
elementType temp;
for (d = n / 2; d > 0; d = d / 2) {
for (i = d; i < n; i++) {
temp = a[i];
for (j = i; j >= d && a[j - d] > temp; j -= d) {
a[j] = a[j - d];
}
a[j] = temp;
}
}
}
在基本的希尔排序中,我们的间隔取 n/2 n/4 n/8 … n/2^i … 1
在上面基本的希尔排序中,最坏的时间复杂度T(n)=O(n^2).很糟糕
下面举一个最坏情况的例子


在介绍堆排序之前,我们先介绍一下选择排序。
选择排序的算法思想:第一次从N个元素中选择一个最小的。放入0位置,第二次从N个元素中选择第二小的,放入1位置。… 第i次从N个元素选择第i小的元素放入第i-1位置
下面是选择排序的伪代码描述
void Selection_Sort ( ElementType A[], int N )
{
for ( i = 0; i < N; i ++ ) {
MinPosition = ScanForMin( A, i, N–1 );
/* 从A[i]到A[N–1]中找最小元,并将其位置赋给MinPosition */
Swap( A[i], A[MinPosition] );
/* 将未排序部分的最小元换到有序部分的最后位置 */
}
}
对于交换元素的操作,是线性。问题在于从N个元素每次找到最i小的元素。选择排序比较暴力,他每次都是从N个元素中选择最小的元素,然后进行交换位置。这样时间时间复杂度T(N)=O(N^2).我们如果改进找到最小元的操作?
答案是使用我们以前学过的工具,最小堆。
算法思想:把用户给定的数组调整成一个最小堆,每次从堆中弹出一个最小的元素,使用临时数组保存,然后在吧临时数组的元素复制回原数组。
伪代码描述:
void Heap_Sort ( ElementType A[], int N )
{
BuildHeap(A); /* O(N) */
for ( i=0; i<N; i++ )
TmpA[i] = DeleteMin(A); /* O(logN) */
for ( i=0; i<N; i++ ) /* O(N) */
A[i] = TmpA[i];
}
通过伪代码我们可以看到,此算法的时间复杂的度为T(N)=O(NlogN),但是他需要开辟一个临时的数组O(N)来存放已经排序好的元素。而且还修养话费元素复制的时间。
算法思想:首先吧数组调整成最大堆。把最大堆的第一个元素和最后一个元素调换位置。这样最大的元素就在原数组的最后。然后吧剩下n-1个元素调整成最大堆。重复上面的操作。这样每次选出最大的元素。
伪代码描述:
void Heap_Sort ( ElementType A[], int N )
{
for ( i=N/2-1; i>=0; i-- )/* BuildHeap */
PercDown( A, i, N );
for ( i=N-1; i>0; i-- ) {
Swap( &A[0], &A[i] ); /* DeleteMax */
PercDown( A, 0, i );
}
}
1.定理:堆排序处理N个不同元素的随机排列的平均比较次数是2N logN - O(Nlog logN) 。
2.虽然堆排序给出最佳平均时间复杂度,但实际效果不如用Sedgewick增量序列的希尔排序。
3.堆排序好处是取出前i个最小的数。
在介绍归并排序的算法之前,我们先来介绍一下“有序子列的归并”下面通过一张图片来介绍
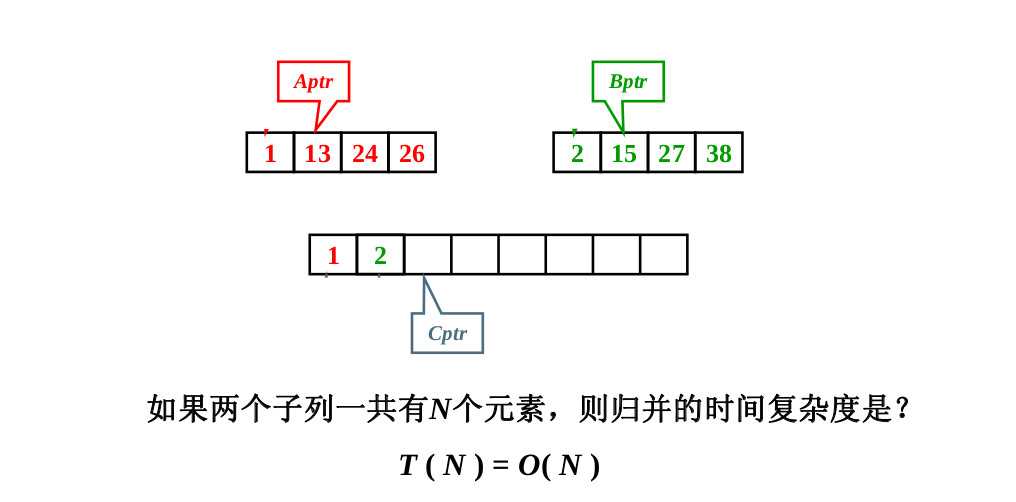
下面是给出有序子列归并的源代码
/*
* Merge sub-sequence to original array.
* @param a original <code>elementType</code> array to store the elements
* @param tmpA temporary <code>elementType</code> array to store the temporary elements
* @param l The start index of left sub-sequence
* @param r The start index of left sub-sequence
* @param rightEnd The end index of left sub-sequence
*/
voidmerge(elementType a[], elementType tmpA[], int l, int r, int rightEnd) {
/*
* lefeEnd is the r-1,the sub-sequence is adjacent
*/
int leftEnd = r - 1;
/*
* tmp is the counter of the <code>tmpA</code>
* we should let <code>tmpA</code> index corresponding original array
*/
int tmp = l;
/*
* Record the quantity of the all elements
*/
int numElements = rightEnd - l + 1;
int i;
while (l <= leftEnd && r <= rightEnd) {
if (a[l] <= a[r]) {
tmpA[tmp++] = a[l++];
} else {
tmpA[tmp++] = a[r++];
}
}
while (l <= leftEnd) {
tmpA[tmp++] = a[l++];
}
while (r < rightEnd) {
tmpA[tmp++] = a[r++];
}
/*
* Put <code>tmpA</code> elements into the original array
*/
for (i = 0; i < numElements; i++, rightEnd--) {
a[rightEnd] = tmpA[rightEnd];
}
}
这个代码的时间复杂度在上面已经说过了,为T(N)=O(N)

这个时间复杂的没有最好,最坏,平均。不论什么样的序列,都是NlogN的时间复杂度。
在归并排序中,我们使用到一个临时数组,那么这个临时数组在哪里分配比较合理?
设想一下,如果我们在merge函数中申请,那会怎么样呢。那就会出现,没调用一次merge函数,我们需要申请和释放这样的一个临时数组。这样申请释放的操作如下图所示:

这样会平凡的对内存进行申请和释放,是很不划算的,而且最后还是要申请一个和N一样大学的数组,那么我们还不如自己在接口函数中把她直接定义好。如下图所示:

虽然我们在一开始归并过程中只会用到临时数组的一小部分,但是总比每次申请释放来的划算。
我们知道递归算法是很消耗系统的堆栈,而且很容易造成内存的溢出。所以我们下面我们使用非递归的方法来实现归并排序。
非递归算法的思想是一开始对数组两两进行归并,然后对两个元素组成的集合在进行两两归并。最后完成数组的排序。下面使用图片来说明
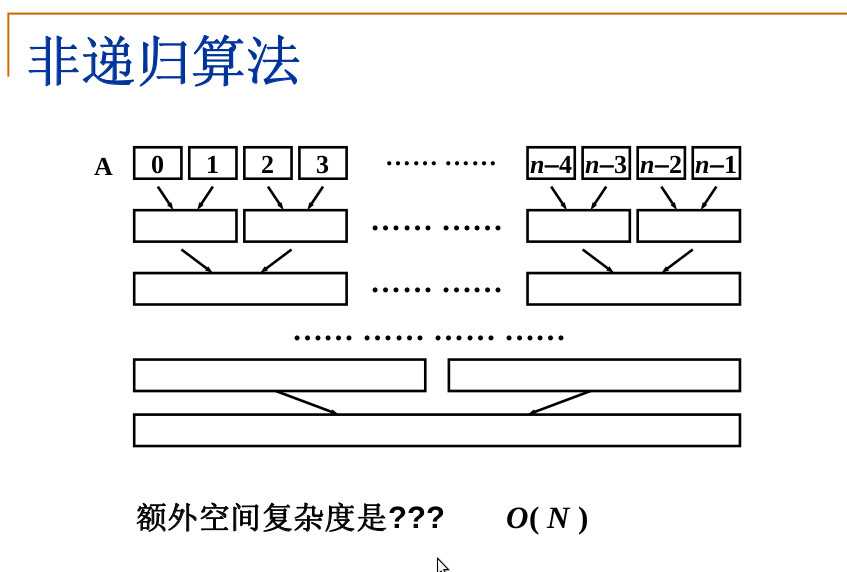
/*
* Use loop method to implement the merge sort
* @param a A integer array need to sort
* @param n The length of the array
*/
voidmerger_SortLoop(elementType a[], int n) {
int length;
elementType *tmpA;
length = 1;
tmpA = malloc(n * sizeof(elementType));
if (tmpA != NULL) {
while (length < n) {
/*
* merge ordered sub-sequence into <code>tmpA</code>
*/
mergerPass(a, tmpA, n, length);
length *= 2;
/*
* merge ordered sub-sequence from <code>tmpA</code> into <code>a</code>
*/
mergerPass(tmpA, a, n, length);
length *= 2;
}
free(tmpA);
} else {
printf("no enough to apply for temporary array");
}
}
给定N个(长整型范围内的)整数,要求输出从小到大排序后的结果。
本题旨在测试各种不同的排序算法在各种数据情况下的表现。各组测试数据特点如下:
数据1:只有1个元素;
数据2:11个不相同的整数,测试基本正确性;
数据3:103个随机整数;
数据4:104个随机整数;
数据5:105个随机整数;
数据6:105个顺序整数;
数据7:105个逆序整数;
数据8:105个基本有序的整数;
数据9:105个随机正整数,每个数字不超过1000。
输入第一行给出正整数N(≤10?5??),随后一行给出N个(长整型范围内的)整数,其间以空格分隔。
在一行中输出从小到大排序后的结果,数字间以1个空格分隔,行末不得有多余空格。
114 981 10 -17 0 -20 29 50 8 43 -5
-20 -17 -5 0 4 8 10 29 43 50 98
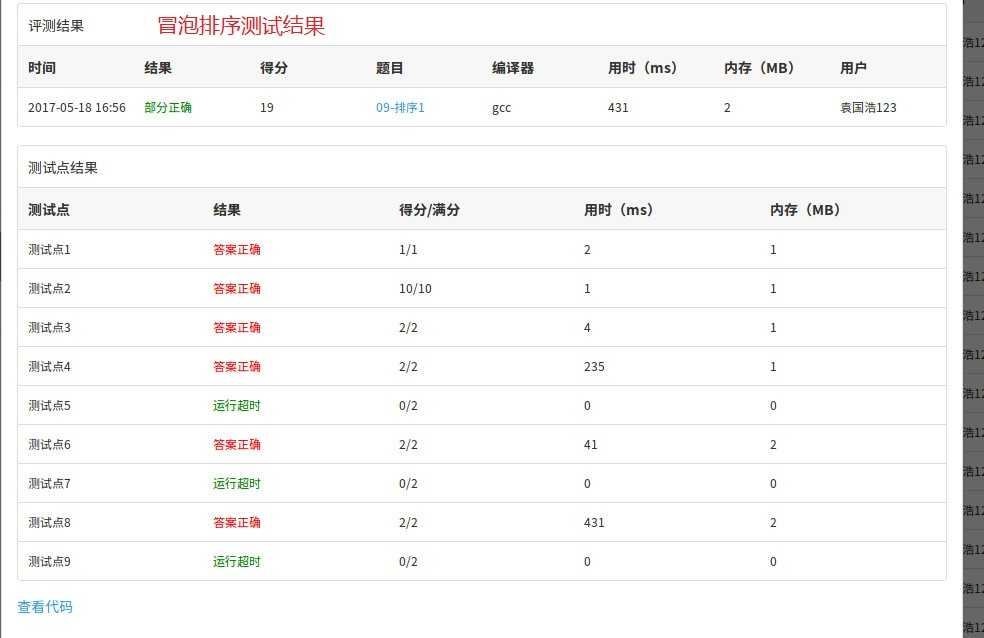
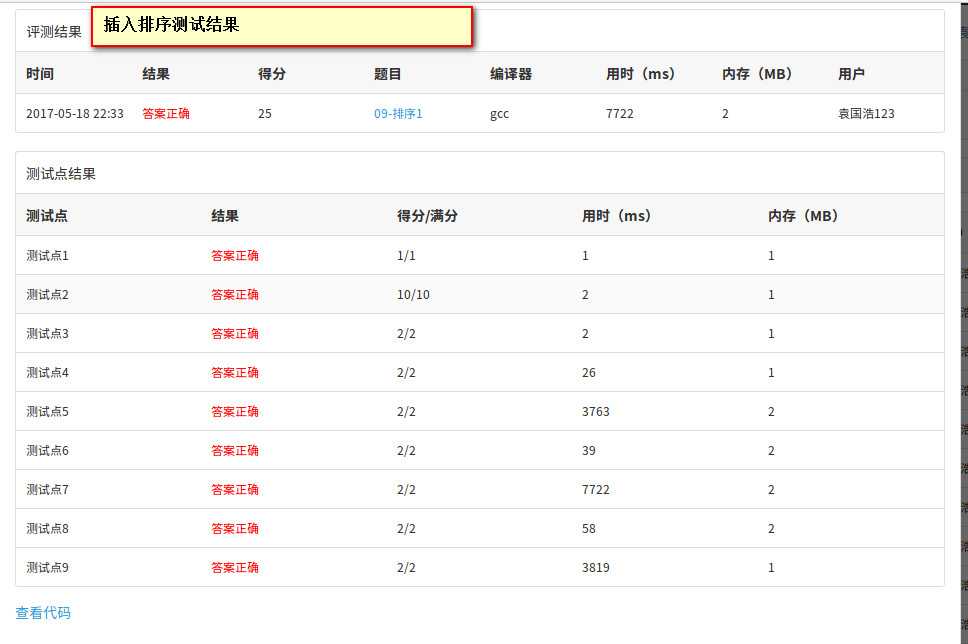
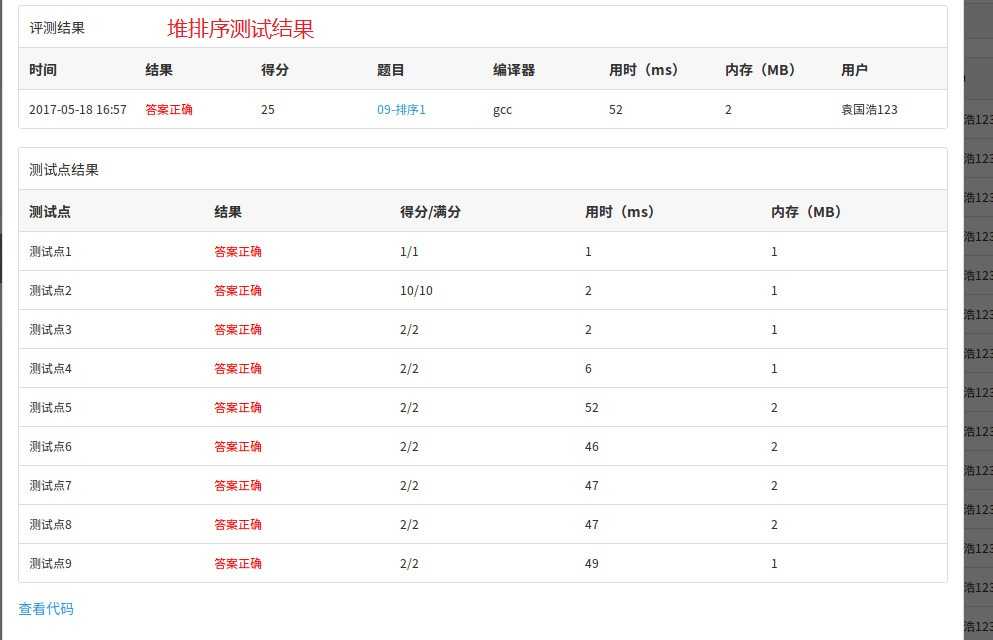
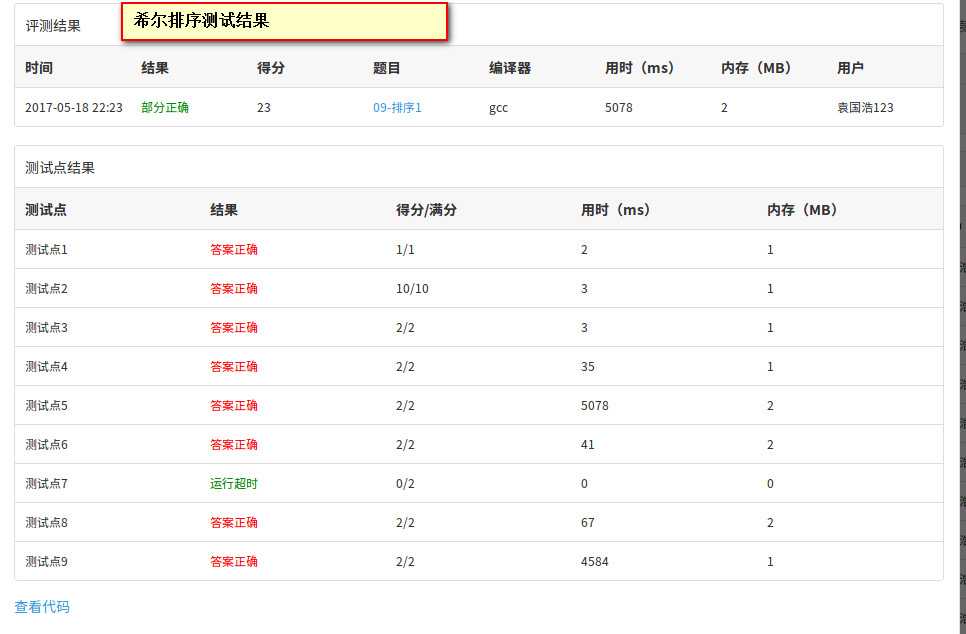
但是希尔排序也有通过的例子
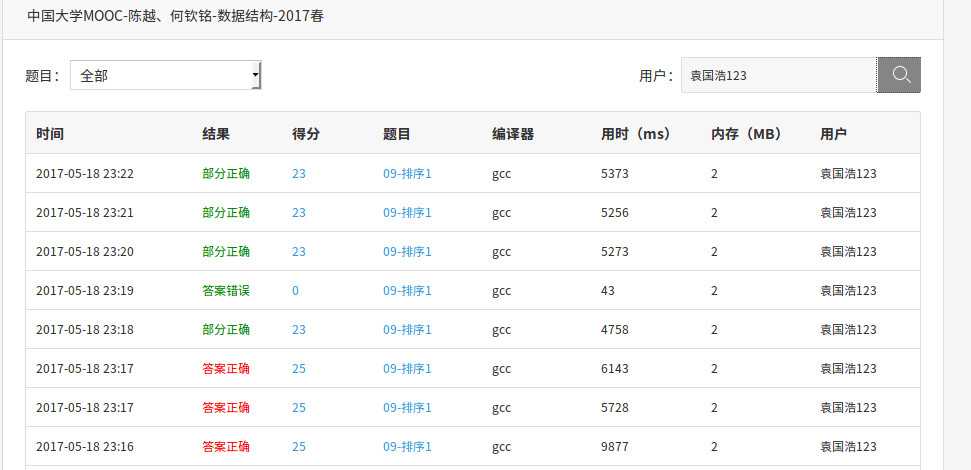
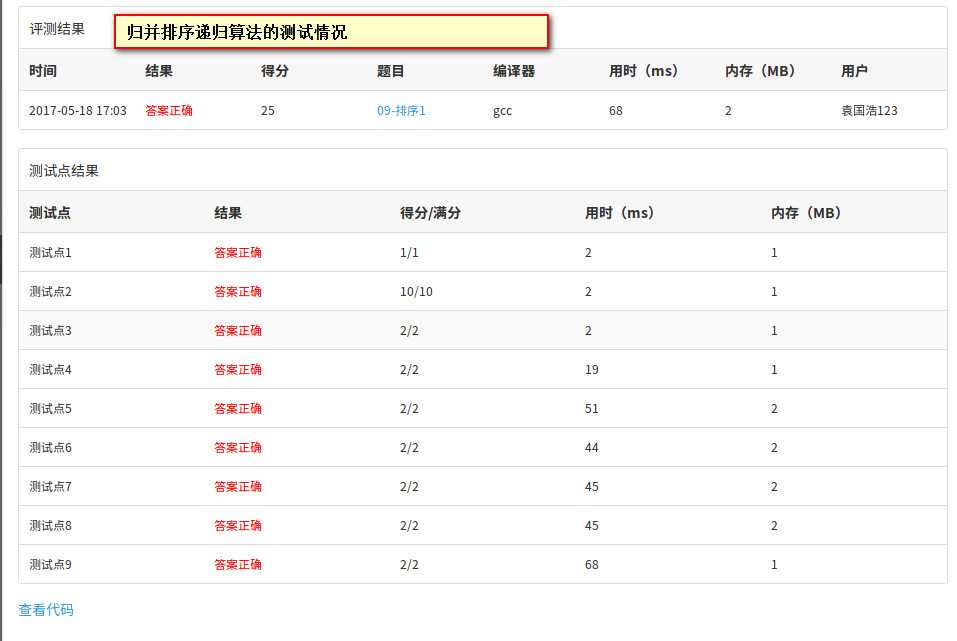
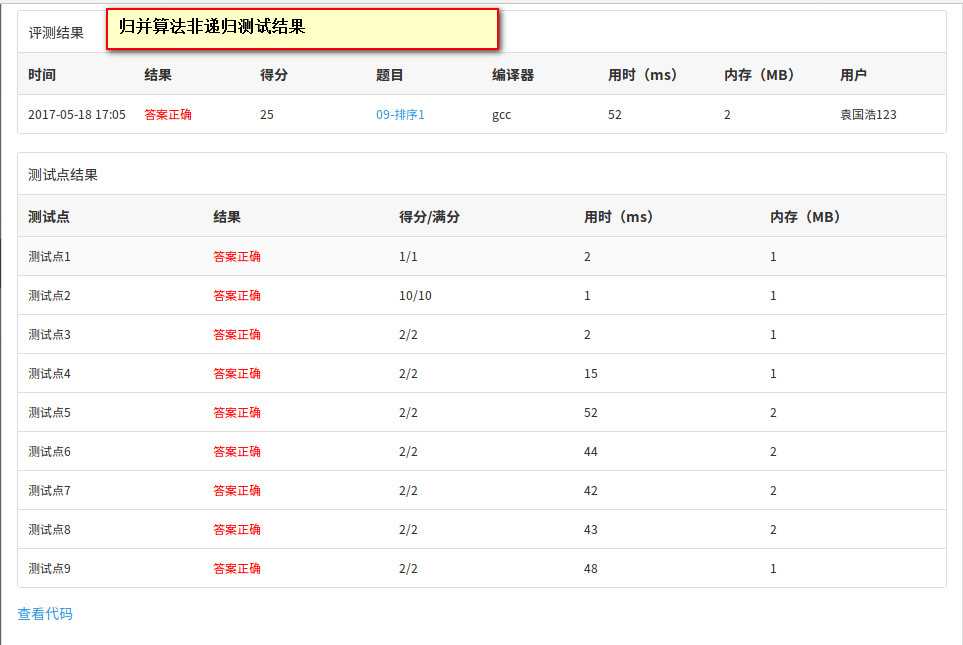
从上面的测试结果来看,堆排序,归并排序都完美通过了测试,而且效率挺高的。
冒泡排序没有通过测试很正常,因为时间复杂度为O(N^2).
是我感到诧异的是,插入排序居然通过了测试,虽然挺耗时,但是希尔排序在测试点7:105个逆序整数竟然没有通过。我的希尔排序使用Sedgewick序列。不是理论上是O(N^(4/3)),怎么会没有通过呢。但是时间复杂度和冒泡排序相近的插入排序居然通过了。好奇怪。而且插入排序在测试点7:105个逆序整数全部是逆序数最坏的时间复杂度为O(N^2),怎么就通过了呢。好奇怪。后来多次对希尔排序进行测试,发现有时候可以通过,有时候没有通过,估计是受机器的影响。感觉希尔排序效率不高,平均的都在5000ms以上

1 /* 2 * bubbleSort.c 3 * 4 * Created on: 2017年5月18日 5 * Author: ygh 6 */ 7 8 #include <stdio.h> 9 10 typedef int elementType; 11 #define MAX_LENGTH 100000 12 13 /* 14 * Swap two integer number value 15 */ 16 void swap(elementType *a, elementType *b) { 17 int temp = *b; 18 *b = *a; 19 *a = temp; 20 } 21 /* 22 * A method to implement bubble sort.If the bubble sort has no any swap 23 * operation at one time,indicating the array has been ordered.So we use a 24 * tag to make it effective 25 *@param a A integer array need to sort 26 *@param n The length of the array 27 */ 28 void bubble_sort(elementType a[], int n) { 29 int i, j, flag; 30 for (i = n - 1; i >= 0; i--) { 31 flag = 0; 32 for (j = 0; j < i; j++) { 33 if (a[j] > a[j + 1]) { 34 swap(&a[j], &a[j + 1]); 35 flag = 1; 36 } 37 } 38 if (flag == 0) { 39 break; 40 } 41 } 42 } 43 44 /* 45 * Print the array to console 46 * @param a A integer array need to sort 47 * @param n The length of the array 48 */ 49 void printArray(int a[], int n) { 50 int i; 51 for (i = 0; i < n; i++) { 52 if (i == n - 1) { 53 printf("%d", a[i]); 54 } else { 55 printf("%d ", a[i]); 56 } 57 } 58 printf("\n"); 59 } 60 61 /* 62 * Get input data from command 63 */ 64 void getInputData(elementType *a, int n) { 65 int i; 66 elementType x; 67 for (i = 0; i < n; i++) { 68 scanf("%d", &x); 69 a[i] = x; 70 } 71 } 72 73 int main() { 74 int a[MAX_LENGTH]; 75 int n; 76 scanf("%d", &n); 77 getInputData(a, n); 78 bubble_sort(a, n); 79 printArray(a, n); 80 return 0; 81 }

1 /* 2 * insertionSort.c 3 * 4 * Created on: 2017年5月18日 5 * Author: ygh 6 */ 7 8 #include <stdio.h> 9 10 #define MAX_LENGTH 100000 11 typedef int elementType; 12 13 /* 14 * Swap two integer number value 15 */ 16 void swap(elementType *a, elementType *b) { 17 int temp = *b; 18 *b = *a; 19 *a = temp; 20 } 21 /* 22 * Implement insertion sort. 23 *@param a A integer array need to sort 24 *@param n The length of the array 25 */ 26 void insertion_sort(elementType a[], int n) { 27 int i, j; 28 elementType temp; 29 for (i = 1; i < n; i++) { 30 temp = a[i]; 31 for (j = i; j > 0 && a[j - 1] > temp; j--) { 32 a[j] = a[j - 1]; 33 } 34 a[j] = temp; 35 } 36 37 } 38 39 /* 40 * Print the array to console 41 * @param a A integer array need to sort 42 * @param n The length of the array 43 */ 44 void printArray(int a[], int n) { 45 int i; 46 for (i = 0; i < n; i++) { 47 if (i == n - 1) { 48 printf("%d", a[i]); 49 } else { 50 printf("%d ", a[i]); 51 } 52 } 53 printf("\n"); 54 } 55 56 /* 57 * Get input data from command 58 */ 59 void getInputData(elementType *a, int n) { 60 int i; 61 elementType x; 62 for (i = 0; i < n; i++) { 63 scanf("%d", &x); 64 a[i] = x; 65 } 66 } 67 68 int main() { 69 int a[MAX_LENGTH]; 70 int n; 71 scanf("%d", &n); 72 getInputData(a, n); 73 insertion_sort(a, n); 74 printArray(a, n); 75 return 0; 76 }

1 /* 2 * shellSort.c 3 * 4 * Created on: 2017年5月18日 5 * Author: ygh 6 */ 7 8 #include <stdio.h> 9 #include <math.h> 10 11 #define MAX_LENGTH 100000 12 typedef int elementType; 13 14 /* 15 * Swap two integer number value 16 */ 17 void swap(elementType *a, elementType *b) { 18 int temp = *b; 19 *b = *a; 20 *a = temp; 21 } 22 23 int getSedgewickStep(int *step, int n) { 24 int i, v1, v2, counter = 0; 25 i = 0; 26 for (i = 0; i < n; i++) { 27 v1 = 9 * pow(4, i) - 9 * pow(2, i) + 1; 28 if (v1 > 0 && v1 < n) { 29 step[counter++] = v1; 30 } 31 v2 = pow(4, i) - 3 * pow(2, i) + 1; 32 if (v2 > 0 && v2 < n) { 33 step[counter++] = v2; 34 } 35 if (v1 > n && v2 > n) { 36 break; 37 } 38 } 39 return counter; 40 } 41 42 /* 43 * A method to implement bubble sort.If the bubble sort has no any swap 44 * operation at one time,indicating the array has been ordered.So we use a 45 * tag to make it effective 46 *@param a A integer array need to sort 47 *@param n The length of the array 48 */ 49 void bubble_sort(int a[], int n) { 50 int i, j, flag; 51 for (i = n - 1; i >= 0; i--) { 52 flag = 0; 53 for (j = 0; j < i; j++) { 54 if (a[j] > a[j + 1]) { 55 swap(&a[j], &a[j + 1]); 56 flag = 1; 57 } 58 } 59 if (flag == 0) { 60 break; 61 } 62 } 63 } 64 65 /* 66 * Implement base shell sort 67 *@param a A integer array need to sort 68 *@param n The length of the array 69 */ 70 void shell_sort_expand_Sedgewick(elementType a[], int n) { 71 int i, j, d, counter, step; 72 elementType temp; 73 int sequence[] = { 1, 5, 19, 41, 109, 209, 505, 929, 2161, 3905, 8929, 74 16001, 6289, 64769 }; 75 counter = 13; 76 /*int sequence[n / 2]; 77 counter = getSedgewickStep(sequence, n); 78 bubble_sort(sequence, counter);*/ 79 /*printArray(sequence, counter); 80 return;*/ 81 for (d = 0; d < counter && sequence[d] < n; d++) { 82 step = sequence[d]; 83 for (i = step; i < n; i++) { 84 temp = a[i]; 85 for (j = i; j >= step && a[j - step] > temp; j -= step) { 86 a[j] = a[j - step]; 87 } 88 a[j] = temp; 89 } 90 } 91 92 } 93 94 /* 95 * Implement base shell sort 96 *@param a A integer array need to sort 97 *@param n The length of the array 98 */ 99 void shell_sort_expand_Sedgewick2(elementType a[], int n) { 100 int i, j, d, counter, step; 101 elementType temp; 102 int sequence[n / 2]; 103 counter = getSedgewickStep(sequence, n); 104 bubble_sort(sequence, counter); 105 for (d = 0; d < counter && sequence[d] < n; d++) { 106 step = sequence[d]; 107 for (i = step; i < n; i++) { 108 temp = a[i]; 109 for (j = i; j >= step && a[j - step] > temp; j -= step) { 110 a[j] = a[j - step]; 111 } 112 a[j] = temp; 113 } 114 } 115 116 } 117 118 /* 119 * Implement base shell sort 120 *@param a A integer array need to sort 121 *@param n The length of the array 122 */ 123 void shell_sort_base(elementType a[], int n) { 124 int i, j, d; 125 elementType temp; 126 for (d = n / 2; d > 0; d = d / 2) { 127 for (i = d; i < n; i++) { 128 temp = a[i]; 129 for (j = i; j >= d && a[j - d] > temp; j -= d) { 130 a[j] = a[j - d]; 131 } 132 a[j] = temp; 133 } 134 } 135 136 } 137 138 /* 139 * Print the array to console 140 * @param a A integer array need to sort 141 * @param n The length of the array 142 */ 143 void printArray(int a[], int n) { 144 int i; 145 for (i = 0; i < n; i++) { 146 if (i == n - 1) { 147 printf("%d", a[i]); 148 } else { 149 printf("%d ", a[i]); 150 } 151 } 152 printf("\n"); 153 } 154 155 /* 156 * Get input data from command 157 */ 158 void getInputData(elementType *a, int n) { 159 int i; 160 elementType x; 161 for (i = 0; i < n; i++) { 162 scanf("%d", &x); 163 a[i] = x; 164 } 165 } 166 167 int main() { 168 int a[MAX_LENGTH]; 169 int n; 170 scanf("%d", &n); 171 getInputData(a, n); 172 shell_sort_expand_Sedgewick2(a, n); 173 printArray(a, n); 174 return 0; 175 }

1 /* 2 * heapSort.c 3 * 4 * Created on: 2017年5月18日 5 * Author: ygh 6 */ 7 8 #include <stdio.h> 9 10 #define MAX_LENGTH 100000 11 typedef int elementType; 12 13 /* 14 * Swap two integer number value 15 */ 16 void swap(elementType *a, elementType *b) { 17 int temp = *b; 18 *b = *a; 19 *a = temp; 20 } 21 22 /* 23 * Update the element of tree make the tree to be a maximal heap 24 * @param a A <code>elementType</code> array to store the elements 25 * @param p The index of the element need to update 26 * @param n The length of the array 27 */ 28 void percDowm(elementType a[], int p, int n) { 29 int parent, child; 30 elementType x; 31 x = a[p]; 32 for (parent = p; (parent * 2 + 1) < n; parent = child) { 33 child = parent * 2 + 1; 34 if ((child != n - 1) && a[child] < a[child + 1]) { 35 child++; 36 } 37 if (x >= a[child]) { 38 break; 39 } else { 40 a[parent] = a[child]; 41 } 42 } 43 a[parent] = x; 44 } 45 46 /* 47 * Implement heap sort 48 * @param a A integer array need to sort 49 * @param n The length of the array 50 */ 51 void heap_sort(elementType a[], int n) { 52 int i; 53 /* 54 * Build max heap 55 */ 56 for (i = n / 2 - 1; i >= 0; i--) { 57 percDowm(a, i, n); 58 } 59 60 /* 61 * Swap and update heap 62 */ 63 for (i = n - 1; i > 0; i--) { 64 swap(&a[0], &a[i]); 65 percDowm(a, 0, i); 66 } 67 } 68 69 /* 70 * Print the array to console 71 * @param a A integer array need to sort 72 * @param n The length of the array 73 */ 74 void printArray(int a[], int n) { 75 int i; 76 for (i = 0; i < n; i++) { 77 if (i == n - 1) { 78 printf("%d", a[i]); 79 } else { 80 printf("%d ", a[i]); 81 } 82 } 83 printf("\n"); 84 } 85 86 /* 87 * Get input data from command 88 */ 89 void getInputData(elementType *a, int n) { 90 int i; 91 elementType x; 92 for (i = 0; i < n; i++) { 93 scanf("%d", &x); 94 a[i] = x; 95 } 96 } 97 98 int main() { 99 int a[MAX_LENGTH]; 100 int n; 101 scanf("%d", &n); 102 getInputData(a, n); 103 heap_sort(a, n); 104 printArray(a, n); 105 return 0; 106 }

1 /* 2 * mergeSort.c 3 * 4 * Created on: 2017年5月18日 5 * Author: ygh 6 */ 7 8 #include <stdio.h> 9 #include <stdlib.h> 10 #define MAX_LENGTH 100000 11 12 typedef int elementType; 13 14 /* 15 * Swap two integer number value 16 */ 17 void swap(elementType *a, elementType *b) { 18 int temp = *b; 19 *b = *a; 20 *a = temp; 21 } 22 23 /* 24 * Merge sub-sequence to original array. 25 * @param a original <code>elementType</code> array to store the elements 26 * @param tmpA temporary <code>elementType</code> array to store the temporary elements 27 * @param l The start index of left sub-sequence 28 * @param r The start index of left sub-sequence 29 * @param rightEnd The end index of left sub-sequence 30 */ 31 void merge(elementType a[], elementType tmpA[], int l, int r, int rightEnd) { 32 /* 33 * lefeEnd is the r-1,the sub-sequence is adjacent 34 */ 35 int leftEnd = r - 1; 36 /* 37 * tmp is the counter of the <code>tmpA</code> 38 * we should let <code>tmpA</code> index corresponding original array 39 */ 40 int tmp = l; 41 /* 42 * Record the quantity of the all elements 43 */ 44 int numElements = rightEnd - l + 1; 45 int i; 46 while (l <= leftEnd && r <= rightEnd) { 47 if (a[l] <= a[r]) { 48 tmpA[tmp++] = a[l++]; 49 } else { 50 tmpA[tmp++] = a[r++]; 51 } 52 } 53 while (l <= leftEnd) { 54 tmpA[tmp++] = a[l++]; 55 } 56 while (r <= rightEnd) { 57 tmpA[tmp++] = a[r++]; 58 } 59 60 /* 61 * Put <code>tmpA</code> elements into the original array 62 */ 63 for (i = 0; i < numElements; i++, rightEnd--) { 64 a[rightEnd] = tmpA[rightEnd]; 65 } 66 } 67 68 /* 69 * Implement the merge sort 70 * @param a original <code>elementType</code> array to store the elements 71 * @param tmpA temporary <code>elementType</code> array to store the temporary elements 72 * @param l The start index of the array which need to sort 73 * @param rightEnd The end index of the array which need to sort 74 */ 75 void mergetSortRecursive(elementType a[], elementType tmpA[], int l, 76 int rightEnd) { 77 int center; 78 if (l < rightEnd) { 79 center = (l + rightEnd) / 2; 80 mergetSortRecursive(a, tmpA, l, center); 81 mergetSortRecursive(a, tmpA, center + 1, rightEnd); 82 merge(a, tmpA, l, center + 1, rightEnd); 83 } 84 } 85 86 /* 87 * Implement merge sort 88 * @param a A integer array need to sort 89 * @param n The length of the array 90 */ 91 void merger_sortRecursive(elementType a[], int n) { 92 elementType *tmpA; 93 tmpA = malloc(n * sizeof(elementType)); 94 if (tmpA != NULL) { 95 mergetSortRecursive(a, tmpA, 0, n - 1); 96 free(tmpA); 97 } else { 98 printf("no enough space to apply for temporary array"); 99 } 100 } 101 102 /* 103 *merge ordered sub-sequence 104 * @param a original <code>elementType</code> array to store the elements 105 * @param tmpA temporary <code>elementType</code> array to store the temporary elements 106 * @param n The length of the a 107 * @param the ordered current sub-sequence length 108 */ 109 void mergerPass(elementType a[], elementType tmpA[], int n, int lenth) { 110 int i, j; 111 /* 112 * The loop will stop when meet the last two ordered sub-sequence 113 * The rest may be two sub-sequence of one sub-sequence 114 */ 115 for (i = 0; i <= n - 2 * lenth; i += lenth * 2) { 116 merge(a, tmpA, i, i + lenth, i + 2 * lenth - 1); 117 } 118 /* 119 *If the rest of is two sub-sequence 120 */ 121 if (i + lenth < n) { 122 merge(a, tmpA, i, i + lenth, n - 1); 123 } else { 124 for (j = i; j < n; j++) 125 tmpA[j] = a[j]; 126 } 127 } 128 129 /* 130 * Use loop method to implement the merge sort 131 * @param a A integer array need to sort 132 * @param n The length of the array 133 */ 134 void merger_SortLoop(elementType a[], int n) { 135 int length; 136 elementType *tmpA; 137 length = 1; 138 tmpA = malloc(n * sizeof(elementType)); 139 if (tmpA != NULL) { 140 while (length < n) { 141 /* 142 * merge ordered sub-sequence into <code>tmpA</code> 143 */ 144 mergerPass(a, tmpA, n, length); 145 length *= 2; 146 /* 147 * merge ordered sub-sequence from <code>tmpA</code> into <code>a</code> 148 */ 149 mergerPass(tmpA, a, n, length); 150 length *= 2; 151 } 152 free(tmpA); 153 } else { 154 printf("no enough to apply for temporary array"); 155 } 156 } 157 158 /* 159 * Print the array to console 160 * @param a A integer array need to sort 161 * @param n The length of the array 162 */ 163 void printArray(int a[], int n) { 164 int i; 165 for (i = 0; i < n; i++) { 166 if (i == n - 1) { 167 printf("%d", a[i]); 168 } else { 169 printf("%d ", a[i]); 170 } 171 } 172 printf("\n"); 173 } 174 175 /* 176 * Get input data from command 177 */ 178 void getInputData(elementType *a, int n) { 179 int i; 180 elementType x; 181 for (i = 0; i < n; i++) { 182 scanf("%d", &x); 183 a[i] = x; 184 } 185 } 186 187 int main() { 188 int a[MAX_LENGTH]; 189 int n; 190 scanf("%d", &n); 191 getInputData(a, n); 192 // merger_sortRecursive(a, n); 193 merger_SortLoop(a, n); 194 printArray(a, n); 195 return 0; 196 }
辛苦一天,数据结构课程的编程练习总算是进入了前100名。付出是值得的

标签:res 6.4 tom rar 序列 分享 type ide 描述
原文地址:http://www.cnblogs.com/yghjava/p/6876197.html