标签:start sizeof 标记 main 新规 images 定义 data ++
一个无向图G的最小生成树就是由该图的那些连接G的所有顶点的边构成的树,且其总价值最低,因此,最小生成树存在的充分必要条件为图G是连通的,简单点说如下:
1.树的定义:有n个顶点和n-1条边,没有回路的称为树
生成树的定义:生成树就是包含全部顶点,n-1(n为顶点数)条边都在图里就是生成树
最小:指的是这些边加起来的权重之和最小
2.判定条件:向生成树中任加一条边都一定构成回路
充分必要条件:最小生成树存在那么图一定是连通的,反过来,图是连通的则最小生成树一定存在
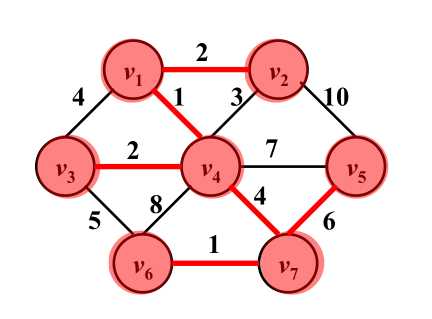
上图的红色的边加上顶点就是原图的一个最小生成树。
给定一个图G,如何计算出该图的最小生成树,最通用的算法有两个,一是Prim算法,二是Kruskal算法,这里先讨论Prim算法。
Prim算法和Dijkstra算法类似,我们对每一个顶点计算值dv和pv以及一个指标,该指标表示该顶点是已知的还是未知的,dv是连接v到已知顶点的最短边的权,pv是导致dv改变的最后的顶点,和Dijkstra算法不同的是dv的更新规则:在每一个顶点v被选取以后,对于每一个与v邻接的未知点w,dw=min{dw,cost(w,v)}.
代码如下:
#include<iostream>
using namespace std;
#define Inf 65535
#define NotAVerter -1
/////////////////////邻接表的相关定义//////////////////////
typedef struct EdgeNode *position;
typedef struct Led_table* Table;
struct EdgeNode //边表结点
{
int adjvex; // 邻接点域,存储该顶点对应的下标
int weight; // 对应边的权值
position next; // 链域,指向下一个邻接点
};
struct Led_table // 邻接表结构
{
int data; //邻接表的大小
position *firstedge; //边表头指针,可以理解为数组
};
//////////////////////////邻接表相关函数定义///////////////
Table Creat_Lable (int MaxElements) //MaxElements参数为希望创建的节点数
{
Table table1 = static_cast<Table> (malloc(sizeof(struct Led_table)));
table1->data = MaxElements;
if (table1 == NULL)
{
cout << "out of space!!!";
}
table1->firstedge = static_cast<position*>(malloc(sizeof(position)*(table1->data)));
if (table1->firstedge == NULL)
{
cout << "out of space!!!";
}
//给每个表头赋值,从0开始
for (int i = 0; i <= table1->data - 1; ++i)
{
table1->firstedge [i] = static_cast<position>(malloc(sizeof(EdgeNode))); //申请一个节点
if (table1->firstedge [i] == NULL)
{
cout << "out of space!!!";
}
table1->firstedge [i]->adjvex = 0;
table1->firstedge [i]->weight = 0; //此参数在此时没有意义
table1->firstedge [i]->next = NULL;
}
return table1;
}
void Insert (Table table1, int v, int w, int weig) //表示存在一条边为<v,w>,且权重为weig
{
position p = static_cast<position>(malloc(sizeof(EdgeNode))); //申请一个节点
if(p == NULL)
{
cout << "out of space!!!";
}
p->adjvex = w;
p->weight = weig;
p->next = table1->firstedge [v]->next;
table1->firstedge [v]->next = p;
}
void Double_Insert (Table table1, int v, int w, int weig) //无向边,双向插入
{
Insert (table1, v, w, weig);
Insert (table1, w, v, weig);
}
/////////////////////最小生成树Prim算法/////////////////////////
typedef struct Prim_tree *Prim_node ;
struct Prim_tree //
{
bool know;
int dist; // 邻接点域,存储该顶点对应的下标
int path; // 对应边的权值
};
Prim_node Prim_init(Table table1, int start) //节点初始化
{
Prim_node Node = static_cast<Prim_node>(malloc(sizeof(Prim_tree)*(table1->data)));
if (Node == NULL)
{
cout << "out of space!!!";
}
for(int i = 0; i != table1->data; ++i)
{
Node[i].know = false;
Node[i].dist = Inf;
Node[i].path = NotAVerter;
}
Node[start].dist = 0; //起点处的距离设为0
return Node;
}
void Prim_Algorithm (Table table1,Prim_node Node) //prim 算法
{
int v;
for (int j = 0; j != table1->data; ++j)
{
int zh = Inf;
for (int i = 0; i != table1->data; ++i) //找路径最小且没有标记过的点
{
if(!Node[i].know && zh > Node[i].dist ) //如果这个点是未知的,且距离比较小
{
zh = Node[i].dist;
v = i;
}
}
Node[v].know = true; //标记这个点
position p = table1->firstedge [v]->next;
while (p != NULL) //
{
if(!Node[p->adjvex].know && Node[p->adjvex].dist > p->weight )
{
Node[p->adjvex].dist = p->weight;
Node[p->adjvex].path = v;
}
p = p->next;
}
}
}
int main ()
{
Table table_1 = Creat_Lable (7); //创建一个大小为7的邻接表
//根据图来为邻接表插入数据
Double_Insert (table_1, 0, 1, 2);Double_Insert (table_1, 0, 2, 4);Double_Insert (table_1, 0, 3, 1);
Double_Insert (table_1, 1, 3, 3);Double_Insert (table_1, 1, 4, 10);
Double_Insert (table_1, 2, 5, 5);
Double_Insert (table_1, 3, 2, 2);Double_Insert (table_1, 3, 5, 8);Double_Insert (table_1, 3, 6, 4);
Double_Insert (table_1, 4, 3, 7);Double_Insert (table_1, 4, 6, 6);
Double_Insert (table_1, 6, 5, 1);
Prim_node Node_1 = Prim_init(table_1, 0); //初始化节点
Prim_Algorithm (table_1,Node_1);
for (int i = 0; i != table_1->data; ++i)
{
cout << Node_1[i].dist << endl;
}
return 0;
}
与Dijkstra算法的代码类似,做点修改就好,该代码所用的例子就是上面的图,计算的结果也是那样的。
夜深了,,,
推荐一首歌《cry on my shoulder》
标签:start sizeof 标记 main 新规 images 定义 data ++
原文地址:http://www.cnblogs.com/1242118789lr/p/6880248.html