标签：nbsp 操作 ddd 访问 程序设计 解法 out bbb next
对一个 有向无环图（Directed Acyclic Graph, DAG） G 进行拓扑排序，是将 G 中的所有顶点排成一个线性序列，
使得图中任意一对顶点 u 和 v，若边 <u,v>∈E(G)，则 u 在线性序列中出现在 v 之前。
通常，这样的线性序列称为满足拓扑次序（Topological Order） 的序列，简称 拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为 拓扑排序。
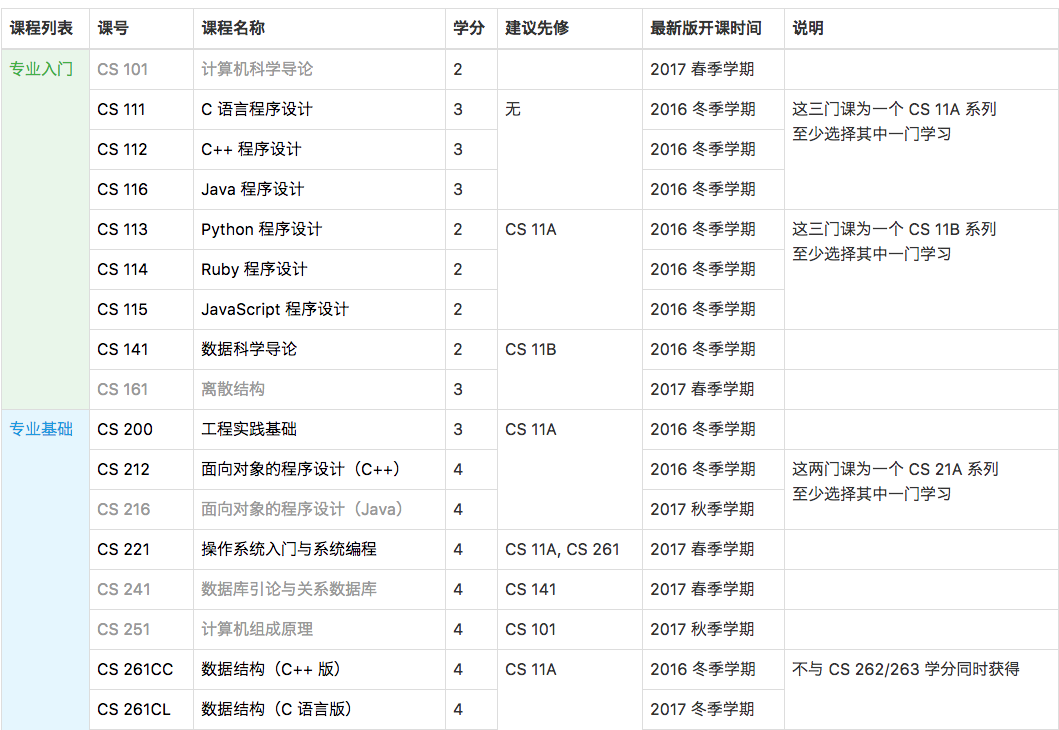
例如，在计蒜客平台上选择软件工程方向，我们会给出一个专业方案列表，如上图。
你需要根据专业方案学习列表上的必修课程和选修课程，而学习每门课程的先决条件是学习完它的全部先修课程。
如学习《数据结构》课程就必须安排在它的先修课程《离散结构》之后。
而学习《C 语言程序设计》课程可以随时安排，因为它是基础课程，没有先修课。
一个符合要求的学习课程的顺序就是对这些课程进行拓扑排序。
拓扑排序算法主要由以下两步循环执行，直到不存在入度为 0 的顶点为止。
循环结束，若输出的顶点数小于图中的顶点数，则表示该图中存在回路，也就是无法进行拓扑排序；否则输出的顶点序列就是一个拓扑序列。
接下来，我们用一个例子来说明这个算法过程。
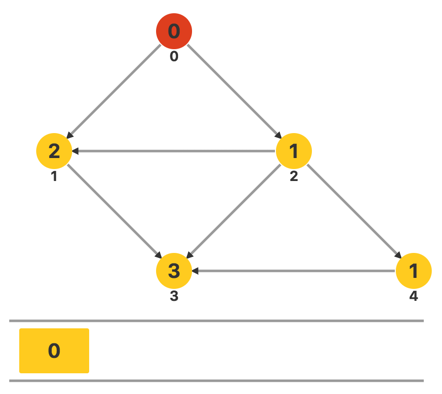
对于如下的图，我们首先算出所有顶点的入度，并找出其中所有入度为零的顶点，发现只有 0，于是我们将 0 插入队列中。
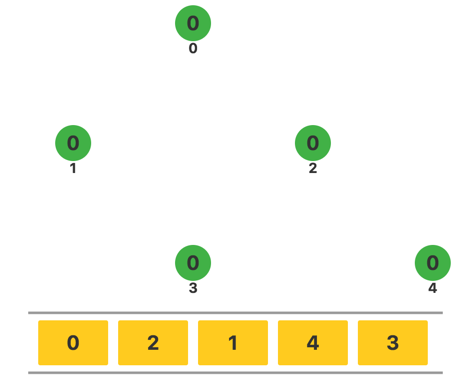
图中圆圈内的数字表示顶点的入度，圆圈下方的数字表示顶点编号，直线表示边，直线一端的箭头表示边的方向。
图的下方是一个队列，用来在拓扑排序时储存所有未处理的入度为零的顶点。
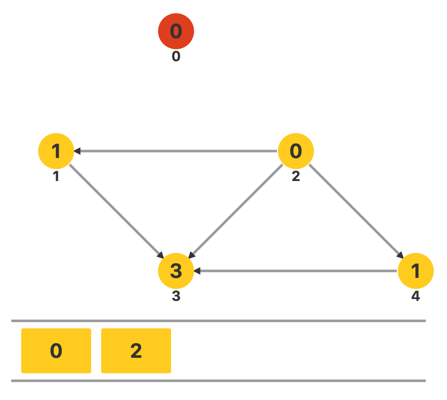
枚举 0 连出的所有边，对于每条边，将另一端的顶点的入度减一。发现有新的入度为零的点 2，则将它们都插入到队列中。
处理完成后将队首元素出队，继续访问当前的队首元素 2。
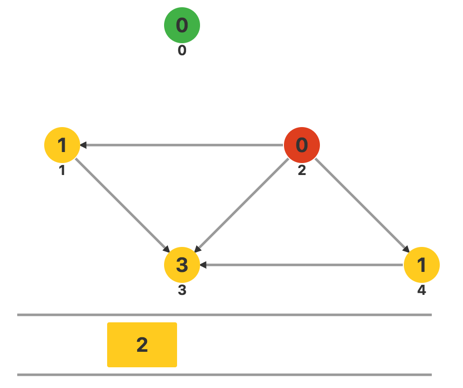
枚举 2 连出的所有边，对于每条边，将另一端的顶点的入度减一。这时发现顶点 1 和顶点 4 的入度均为零，将它们都插入队列。
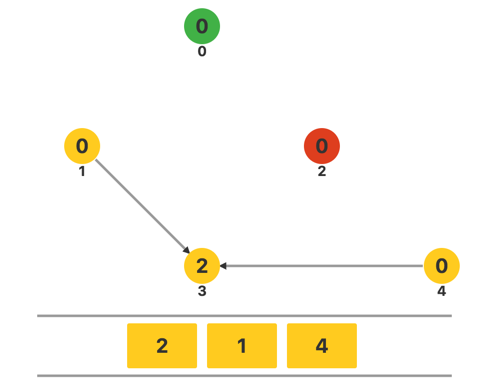
处理完成后将队首元素出队，继续访问当前的队首元素 1。
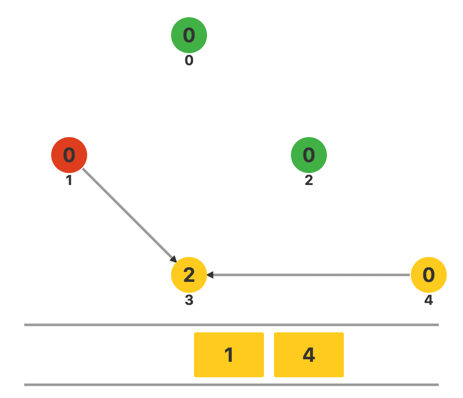
枚举 1 连出的所有边，修改对应的入度。
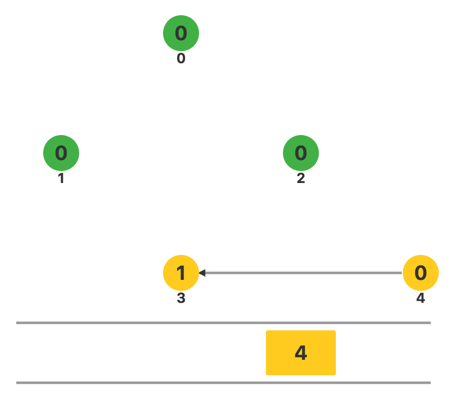
将 1 出队，继续访问当前的队首元素 4，调整对应顶点的入度。发现顶点 3 的入度为零，将它插入队列中。
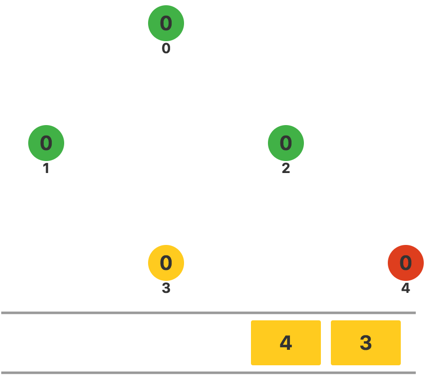
将 4 出队，目前队首顶点为 3，发现没有和它相邻的顶点，将其出队。此时队列为空，算法结束。
我们发现，这 5 个顶点已经都访问过了，所以最终顶点入队的顺序就是这张有向图的一个拓扑排序。
基于邻接表的 C++ 示例代码如下：
struct edge {
int v, next;
} e[MAX_M];
int p[MAX_N], eid;
int topo() {
queue<int> q;
for (int i = 1; i <= n; i++) {
if (indegree[i] == 0) { // 将所有入度为零的顶点入队
q.push(i);
}
}
while (!q.empty()) {
int now = q.front();
cout << "visiting " << now << endl;
q.pop();
for (int i = p[now]; i != -1; i = e[i].next) {
int v = e[i].v;
indegree[v]--;
if (indegree[v] == 0) { // 将入度新变成零的顶点入队
q.push(v);
}
}
}
}
将若干个由字母组成的矩形叠加到一起，给定最终的叠加效果，求出一个合法的叠放次序。保证每个矩形只由一种字母组成，宽度为 11，且不同矩形对应的字母各不相同。
........ ........ ........ ........ .CCC....
EEEEEE.. ........ ........ ..BBBB.. .C.C....
E....E.. DDDDDD.. ........ ..B..B.. .C.C....
E....E.. D....D.. ........ ..B..B.. .CCC....
E....E.. D....D.. ....AAAA ..B..B.. ........
E....E.. D....D.. ....A..A ..BBBB.. ........
E....E.. DDDDDD.. ....A..A ........ ........
E....E.. ........ ....AAAA ........ ........
EEEEEE.. ........ ........ ........ ........
1 2 3 4 5
例如，对于上面这 5 个矩形，有如下的最终叠放效果：
.CCC....
ECBCBB..
DCBCDB..
DCCC.B..
D.B.ABAA
D.BBBB.A
DDDDAD.A
E...AAAA
EEEEEE..
保证每个矩形的四条边上最终都至少出现一个点。
解法：拓扑排序题目的关键，在于建立实际问题和图中有向边的对应关系。
由于题目保证，我们可以获得每个矩形四条边在图中占据的位置。
如果两个矩形有公共点，例如矩形A和B，它们的公共点最终显示的是B，因此B一定在A之后放入。
我们就可以从A点向B点连一条有向边。最终建立的有向图如下所示：
对于这张有向图，存在合法拓扑序列：E,D,A,B,C，这也就是合法的放入顺序。
标签：nbsp 操作 ddd 访问 程序设计 解法 out bbb next
原文地址：http://www.cnblogs.com/wangkaipeng/p/6881911.html
