标签:sha 左右 div ext attr bsp com 准备工作 平衡二叉树
二叉树是每个节点最多有两个子树的树结构
(1)完全二叉树——若设二叉树的高度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二 叉树。
(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。
(3)平衡二叉树——平衡二叉树又被称为AVL树,它是一棵二叉排序树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
二叉数遍历 有 前序遍历、中序遍历、后续遍历,层次遍历、Z型遍历
1.定义树的结构
public class Tree
{
public string Value;
public Tree Left;
public Tree Right;
}
2.创建一颗二叉树
public static Tree CreatTree()
{
Tree tree = new Tree() { Value = "A" };
tree.Left = new Tree()
{
Value = "B",
Left = new Tree() { Value = "D" },
Right = new Tree() { Value = "E", Right = new Tree() { Value = "H" } }
};
tree.Right = new Tree() { Value = "C", Left = new Tree() { Value = "F" }, Right=new Tree() { Value="G"} };
return tree;
}
树的效果图如下
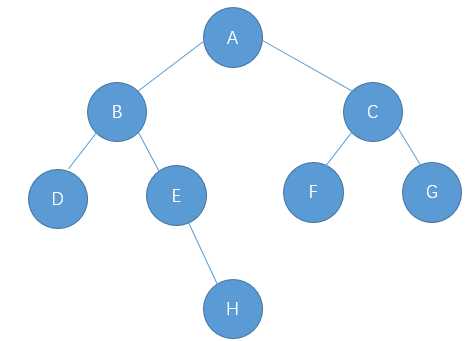
前序遍历首先访问根结点然后遍历左子树,最后遍历右子树。在遍历左、右子树时,仍然先访问根结点,然后遍历左子树,最后遍历右子树
前序遍历结果 A->B->D->E->H->C->F->G
C#实现二叉树的前序遍历
public static void PreOrder(Tree tree)
{
Console.Write(tree.Value + " ");
if (tree.Left != null)
{
PreOrder(tree.Left);
}
if (tree.Right != null)
{
PreOrder(tree.Right);
}
}
中序遍历也叫做中根遍历、中序周游,遍历方式是先左后根再右
中序遍历结果 D->B->E->H->A->F->C->G
看代码
public static void InOrder(Tree tree)
{
if (tree.Left != null)
{
InOrder(tree.Left);
}
Console.Write(tree.Value + " ");
if (tree.Right != null)
{
InOrder(tree.Right);
}
}
后序遍历也叫做后根遍历、后序周游,可记做左右根。先左后右再根。巧记:左右根。
后序遍历首先遍历左子树,然后遍历右子树,最后访问根结点,在遍历左、右子树时,仍然先遍历左子树,然后遍历右子树,最后遍历根结点
后序遍历结果 D->H->E->B->F->G->C->A
看代码
public static void InOrder(Tree tree)
{
if (tree.Left != null)
{
InOrder(tree.Left);
}
Console.Write(tree.Value + " ");
if (tree.Right != null)
{
InOrder(tree.Right);
}
}
层次遍历就是按照树的层次从上到下进行输出,层次遍历我们可以借助队列的先进先出
看代码
public static void LevelOrder(Tree tree)
{
var queue = new Queue<Tree>();
queue.Enqueue(tree);
while (queue.Any())
{
var item = queue.Dequeue();
Console.Write(item.Value);
if (item.Left != null)
{
queue.Enqueue(item.Left);
}
if (item.Right != null)
{
queue.Enqueue(item.Right);
}
}
}
标签:sha 左右 div ext attr bsp com 准备工作 平衡二叉树
原文地址:http://www.cnblogs.com/zhaodayou/p/6883147.html