标签:不为 person 最短路 arc 构建 apu end 最短路径 cti
下面我们来来BFS算法策略:
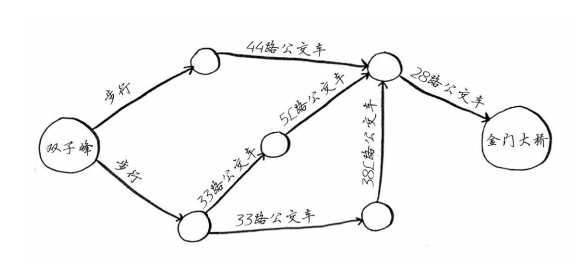
比如:我们要从双子峰---->金门大桥,最短路径如何?
我们利用广度优先搜索来一步步求解,注意广度优先搜索在于的关键在于“广”,也就是说以双子峰为起点,我们要尽可能的多比较与之相邻的周边路径,从其中选取一条最优路径。
第一步:
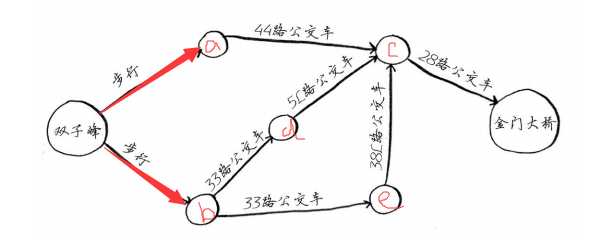
我们沿着两个箭头方向路径探索到a点和b点后,发现并没有到达想要去的地方,于是我继续往下探索。
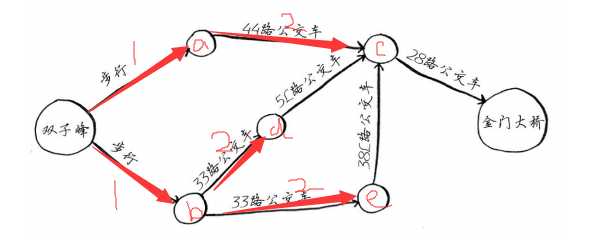
同样,我们发现还没有到达目的地,继续往下探索。
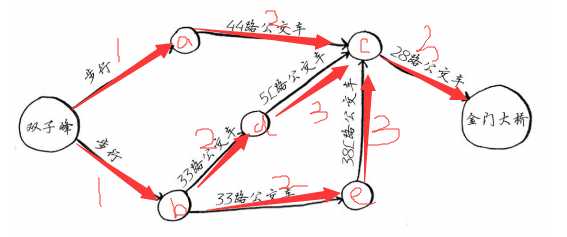
到达这一步后,我们发现其中有一条路径已经到达金门大桥,而其他两条路径仅仅到达c点。因此,我们寻找到的最短路径为:双子峰->a->c->金门大桥。
所以,由上我们可以知道,广度优先搜索其实就是用来探索最短路径的一种方式。
根据上面实例,我们想要寻找一条到某地的最短路径,需要一下两个步骤:
(1)使用图来建立问题模型。
(2)使用广度优先搜索解决问题。
利用广度优先搜索,我们可以回答两个问题:
1.从节点A出发,有前往B节点的路径吗?
2.从节点A出发,前往B节点哪条路径最短?
首先,我们来看看如何构建一张图。
这里我们要使用一种能够表示映射关系的数据结构---散列表。至于什么是散列表,这里就不再赘述。
例如:
graph = {}
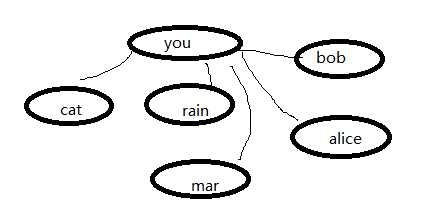
grapu[‘you‘] = [‘alice‘,‘bob‘,‘mar‘,‘rain‘,‘cat‘]
这里的“you”被映射到一个数组。在‘you‘的这个数组里面,包含所有与你相邻的元素。
有了以上方式,我们就可以构建一张更大图。
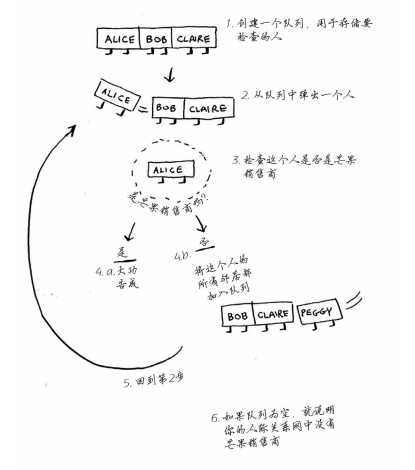
首先,创建一个双端队列,将需要查找的压入队列中。
from collections import deque
def person_is_seller(name):
return name[-1] == ‘m‘ #如果这个名字是以M结尾,则是
graph = {}
grapu[‘you‘] = [‘alice‘,‘bob‘,‘mar‘,‘rain‘,‘cat‘]
search_queue = deque() #创建一个队列
search_queue += graph[‘you‘] #将you压入队列
while search_queue: #只要队列不为空
person = search_queue.popleft() #取出左边第一个人
if person_is_seller(person): #检查这个人是否为芒果商
print person += ‘ is a mango seller! ‘
return True
else:
search_queue += graph[person] #将这个人的朋友加入队列
return False #没有芒果商
但是,上面算法有一个明显的问题,如果你的朋友alice和bob都有这一个好友,那么在查找的过程中就会陷入循环状态。要解决这个问题,我们可以设置一个列表,来标记那些已经被查找过的人。因此,最终代码如下:
def search(name):
search_queue = deque() #创建一个队列
search_queue += graph[name] #将需要查找的压入队列
searcher = [] # 用于记录已经查找过的
while search_queue: #只要队列不为空
person = search_queue.popleft() #取出左边第一个人
if not person in searched: #当这个人不在searched中才继续往下查找
if person_is_seller(person): #检查这个人是否为芒果商
print person += ‘ is a mango seller! ‘
return True
else:
search_queue += graph[person] #将这个人的朋友加入队列
searched.append(person)
return False #没有芒果商
首先沿着每条边进行查找,如果边数为n,查找效率为O(V)
再次,我们在每次查找过程中需要对已经搜索的列表进行二次判断,判断所需时间为P(n)
因此,广度优先搜索总的查找效率为O(V+n)
标签:不为 person 最短路 arc 构建 apu end 最短路径 cti
原文地址:http://www.cnblogs.com/vipchenwei/p/6882593.html