标签:基础 UI uil sem 技术 int 广度优先遍历 param while
package cn.xf.algorithm.ch03;
import java.util.ArrayDeque;
import java.util.Iterator;
import java.util.Queue;
import org.junit.Test;
/**
*
* 功能:广度优先遍历
* @author xiaofeng
* @date 2017年5月21日
* @fileName BFS.java
*
*/
public class BFS {
public void breadthFirstSearch(int graph[][], char points[], int marks[]) {
//初始化所有标记
for(int i = 0; i < marks.length; ++i) {
marks[i] = 0;
}
//遍历所有节点
for(int i = 0; i < points.length; ++i) {
//判断是否已经遍历被标记,如果没有,就作为一个新的树的起始节点
if(marks[i] == 0) {
//没有被标记
StringBuilder paths = new StringBuilder(points[i] + "");
//开始广度遍历
marks[i] = 1;
bfsc(graph, points, marks, i, paths);
System.out.println(paths.toString());
}
}
}
/**
* 广度优先遍历一颗树
* @param graph
* @param points
* @param marks
* @param firstIndex
* @param paths
*/
public void bfsc(int graph[][], char points[], int marks[], int firstIndex, StringBuilder paths) {
//创建队列,存放当前节点的所有子女节点,索引
Queue queue = new ArrayDeque<Integer>();
queue.add(firstIndex);
//下层的子女节点的所有集合
//遍历队列,并且把下级子节点添加到新队列中,等待下次遍历
//只要队列不为空,就不点遍历,到叶子节点
while(!queue.isEmpty()) {
//取出当前的前向节点,遍历其下所有子女节点,队列中有数据
//获取并移除此双端队列所表示的队列的头
int temp = (Integer) queue.poll(); //获取队列头
//获取其后面的可达节点
for(int i = 0; i < points.length; ++i) {
int arrayNum = graph[temp][i]; //是否可达,并且还要判断是否已经被标记
if(marks[i] == 0 && arrayNum != 0) {
//如果这个节点可达并且没有被标记,就把这个节点添加到队列中
paths.append(" => " + points[i]);
marks[i] = 1; //从新标记节点
queue.add(i);
}
}
}
}
@Test
public void test1() {
BFS bfs = new BFS();
//a,b,c,d,e,f,g,h,i,j一共10个节点,两颗树
//以下是矩阵图,0表示不相连,1表示相连,节点本身自己到自己为0
int graph[][] = {
// a,b,c,d,e,f,g,h,i,j
{0,0,1,1,1,0,0,0,0,0}, //a 到其他节点
{0,0,0,0,1,1,0,0,0,0}, //b 到其他节点
{1,0,0,1,0,1,0,0,0,0}, //c 到其他节点
{1,0,1,0,0,0,0,0,0,0}, //d 到其他节点
{1,1,0,0,0,1,0,0,0,0}, //e 到其他节点
{0,1,1,0,1,0,0,0,0,0}, //f 到其他节点
{0,0,0,0,0,0,0,1,0,1}, //g 到其他节点
{0,0,0,0,0,0,1,0,1,0}, //h 到其他节点
{0,0,0,0,0,0,0,1,0,1}, //i 到其他节点
{0,0,0,0,0,0,1,0,1,0} //j 到其他节点
};
char points[] = {‘A‘, ‘B‘, ‘C‘, ‘D‘, ‘E‘, ‘F‘, ‘G‘, ‘H‘, ‘I‘, ‘J‘};
int marks[] = {0,0,0,0,0,0,0,0,0,0};
bfs.breadthFirstSearch(graph, points, marks);
}
}
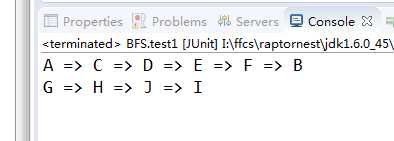
结果:
标签:基础 UI uil sem 技术 int 广度优先遍历 param while
原文地址:http://www.cnblogs.com/cutter-point/p/6885937.html