拓扑排序讲解

标签：所有结点   选择   枚举   例题   基础   先来   color   href   learning   

在这里我们要说的拓扑排序是有前提的

        我们在这里说的拓扑排序是基于有向无环图的！！！。

(⊙o⊙)…我所说的有向无环图都知道是什么东西吧。。

如果不知道，我们下面先来来说说什么是有向无环图。

所谓有向无环图，顾名思义是不存在环的有向图（至于有向图是什么不知道的在前面我们有一个图论讲解上都有）。

点的入度：以这个点为结束点的边数。

点的出度：以这个点为出发点的边的条数。

拓扑序就是对于一个节点的一个排列，使得（u，v）属于E，那么u一定出现在v的前面。然而拓扑排序就是一个用来求拓扑序的东西。

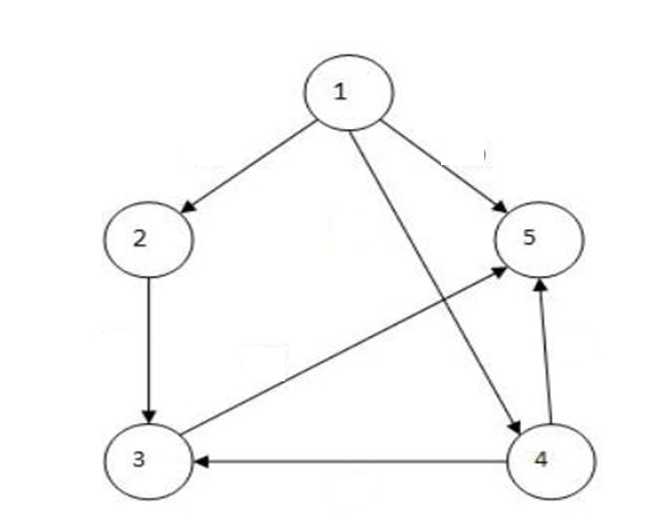对于左面的这个图，一个合法的拓扑序是（1,2,4,3,5）。

又有一个问题了，知道了这些东西后，我们又要怎样求一个有向无环图的拓扑序呢？

我们可以观察到拓扑排序的定义是：若(u,v)∈E，那么u在排列中出现的位置一定在v前面。

也就是说，考虑一个节点u，当我们删除u在序列中处于他前面的所有点之后，u的入度应该是0.

因此，我们就得到了一个拓扑排序的大致的算法思路。

具体怎么着呢  ？。？

循环n次

    选定一个入度为0且仍存在（未出现在序列中）的点v

　 删除点v以及从从点v出发的所有边，更新剩余点的入度

重复上述过程，这样我们就可以得到一个合法的拓扑序。

既然这样，我们就总结下拓扑排序的精髓吧。

精髓（具体方法）：
⑴ 从图中选择一个入度为0的点加入拓扑序列。
⑵ 从图中删除该结点以及它的所有出边（即与之相邻点入度减1）。
反复执行这两个步骤，直到所有结点都已经进入拓扑序列。

还可不可以消化得了？

如果还不可以的话，下面我们就来具体讲一讲拓扑排序吧。

参考博客：http://blog.csdn.net/dm_vincent/article/details/7714519

一。定义

将有向图中的顶点以线性方式进行排序。即对于任何连接自顶点u到顶点v的有向边uv，在最后的排序结果中，顶点u总是在顶点v的前面。

如果这个概念还略显抽象的话，那么不妨考虑一个非常非常经典的例子——选课。我想任何看过数据结构相关书籍的同学都知道它吧。假设我非常想学习一门机器学习的课程，但是在修这么课程之前，我们必须要学习一些基础课程，比如计算机科学概论，C语言程序设计，数据结构，算法等等。那么这个制定选修课程顺序的过程，实际上就是一个拓扑排序的过程，每门课程相当于有向图中的一个顶点，而连接顶点之间的有向边就是课程学习的先后关系。只不过这个过程不是那么复杂，从而很自然的在我们的大脑中完成了。将这个过程以算法的形式描述出来的结果，就是拓扑排序。

二。代码实现

#include <bits/stdc++.h>
using namespace std;

const int maxn=100000+15;
struct Edge
{
    int x,y,next;
    Edge(int x=0,int y=0,int next=0):
    x(x),y(y),next(next) {}
}edge[maxn];
int n,m,head[maxn],sumedge,inn[maxn];
int ins(int x,int y)
{
    edge[++sumedge]=Edge(x,y,head[x]);
    return head[x]=sumedge;
}
int Head,tail,que[maxn];
int main()
{
    scanf("%d%d",&n,&m);
    for (int i=1;i<=m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        ins(x,y);
        inn[y]++;
    }
    Head=1;tail=0;
    for (int i=1;i<=n;i++)
     if (inn[i]==0) que[++tail]=i;//如果该点的入度为0,删掉与这个点相连的点,删后如果入度为0的话,把该点入队 .
    for (;Head<=tail;Head++)//循环枚举与该点相连的点，把该点入队。 
    {//循环上述过程，直到说有的点都入队（有向无环图，每一个点肯定都与一个点相连，这样我们重复这个过程，就可以很好地把所有的带点都考虑到，如此一来，所有的点就都入队了。 
        int x=que[Head];
        for (int u=head[x];u;u=edge[u].next)
        {
            inn[edge[u].y]--;//删掉与这个点相连的点
            if (inn[edge[u].y]==0)// 删后如果入度为0的话
             que[++tail]=edge[u].y;//把该点入队 
        }
    }
    return 0;
}

就说这些吧，我们在下面还会再说几个例题。（那就请看下一页吧）

拓扑排序讲解

标签：所有结点   选择   枚举   例题   基础   先来   color   href   learning   

原文地址：http://www.cnblogs.com/z360/p/6891705.html