标签:scan namespace com open name 否则 访问 string ++
Fleury算法看这里 http://hihocoder.com/problemset/problem/1181

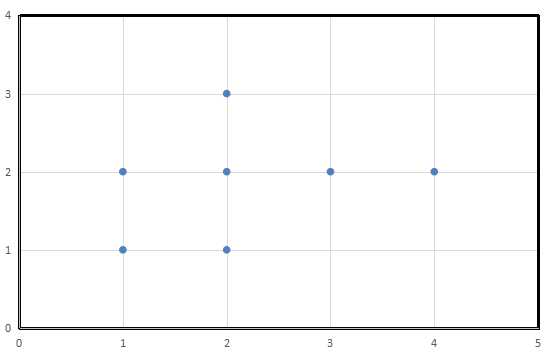
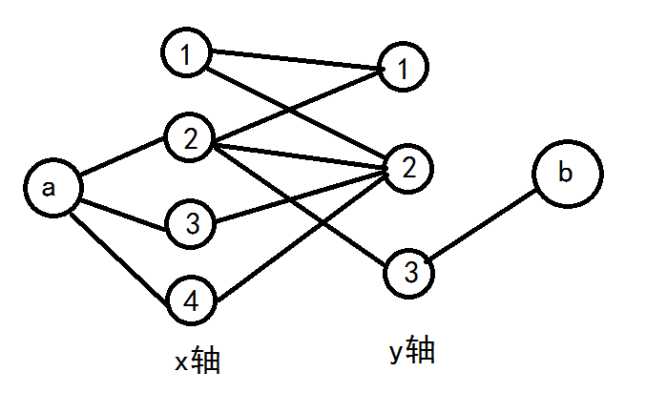
把每个点看成边,每个横纵坐标看成一个点,得到一个无向图.
如果新图中每个点的度都是偶数,那么就是一个欧拉图,对该图跑一遍欧拉回路,对走过的边轮流染色,就可以保证每个点所连的边的红蓝颜色相等.
如果存在度数为奇数的点,新建两个点a和b.把横坐标的度数为奇数的点和a连边,把纵坐标为奇数的点和b连边,这样最多只有a和b的度数为奇数,可以跑欧拉路径.

注意Fleury算法的时候,要及时把访问过的边从图中删去(真的删去而不是打标记),否则重复访问会导致复杂度飙升。
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
struct Edge{
int v,id;
};
vector<Edge>G[400010];
int n,S,T;
bool anss[200010],pen,vis[600010];
inline void dfs(int U){
while(!G[U].empty()){
Edge e=G[U].back();
G[U].pop_back();
if(!vis[e.id]){
vis[e.id]=1;
dfs(e.v);
if(e.id<=n){
anss[e.id]=pen;
pen^=1;
}
}
}
}
int main(){
// freopen("c.in","r",stdin);
int x,y;
scanf("%d",&n);
S=400001; T=400002;
for(int i=1;i<=n;++i){
scanf("%d%d",&x,&y);
G[x].push_back((Edge){y+200000,i});
G[y+200000].push_back((Edge){x,i});
}
int cnt=n;
for(int i=1;i<=200000;++i){
if(G[i].size()&1){
G[S].push_back((Edge){i,++cnt});
G[i].push_back((Edge){S,cnt});
}
}
for(int i=200001;i<=400000;++i){
if(G[i].size()&1){
G[i].push_back((Edge){T,++cnt});
G[T].push_back((Edge){i,cnt});
}
}
if(G[S].size()&1){
dfs(S);
}
if(!G[T].empty()){
dfs(T);
}
for(int i=1;i<=200000;++i){
if(!G[i].empty()){
dfs(i);
}
}
for(int i=1;i<=n;++i){
putchar(anss[i] ? ‘r‘ : ‘b‘);
}
puts("");
return 0;
}
【欧拉回路】【欧拉路径】【Fleury算法】CDOJ1634 记得小苹初见,两重心字罗衣
标签:scan namespace com open name 否则 访问 string ++
原文地址:http://www.cnblogs.com/autsky-jadek/p/6910331.html