标签:proc com 改变 注意 存在 其他 解决 end 组合
●如果任意枚举矩形坐标,显然不可行。数组太大,开不下!
●我们注意到,如果我们放入了矩形,矩形周围并没有其它矩形,那么稍微移动这个矩形,不会改变答案。
显然,一定存在一种方案,使得放入的矩形的边界与某些已知矩形边界重合。
我们不妨规定,放入的矩形下边界必须与已知矩形重合、左边界必须与已知矩形重合。
所以就可以做了
1 type rec=record 2 x1,y1,x2,y2:longint; 3 end; 4 var n,x,y,i,j,k,ans,max,xx,yy:longint; 5 a:array[1..10000]of rec; 6 begin 7 assign(input,‘rectangle.in‘); 8 assign(output,‘rectangle.out‘); 9 reset(input); 10 rewrite(output); 11 readln(n,x,y); 12 for i:=1 to n do 13 readln(a[i].x1,a[i].y1,a[i].x2,a[i].y2); 14 for i:=1 to n do 15 for j:=1 to n do begin 16 xx:=a[i].x1; yy:=a[j].y1; 17 ans:=0; 18 for k:=1 to n do 19 if (a[k].x1>=xx)and(a[k].x1<=xx+x)and(a[k].y1>=yy)and(a[k].y2<=yy+y) 20 and(a[k].x2>=xx)and(a[k].x2<=xx+x)and(a[k].y2>=yy)and(a[k].y2<=yy+y)
//这里是判断以第i个矩形的左下角坐横标X1,第j个矩形的左下角纵坐标Y1围成的X*Y的矩形能不能覆盖第k个矩形
21 then inc(ans);
22 if ans>max then max:=ans;
23 end;
24 writeln(max);
25 close(input);
26 close(output);
27 end.
对于目前已经实现的算法的平均时间复杂度为O(length(s)*k/2)或许更少,
但是实在想不出办法来优化,于是就这样放在这里吧!
1 var k,i,ans:longint; 2 s:ansistring; 3 function check(l,r:longint):boolean;//判断字符串s从l位到r位是否为回文 4 var th:ansistring; 5 i:longint; 6 begin 7 th:=‘‘; 8 for i:=l to r do th:=th+s[i]; 9 for i:=1 to length(th)div 2+1 do 10 if th[i]<>th[length(th)-i+1] then exit(false); 11 exit(true); 12 end; 13 begin 14 assign(input,‘palin.in‘); 15 assign(output,‘palin.out‘); 16 reset(input); 17 rewrite(output); 18 readln(k); 19 readln(s); 20 for i:=1 to length(s) do begin 21 if i+k-1>length(s) then break; 22 if check(i,i+k-1) then inc(ans); 23 end;//枚举当前点和后面连这个点加起来为k位是否为回文
24 writeln(ans);
25 close(input);
26 close(output);
27 end.
一开始想的复杂,选排快排一起用太复杂了点。暴力好像拿了92分!
现在讲一种很简单的办法!
排序+枚举(排序:按照简单-中等-困难的顺序输出)
解决方法是:先从小到大枚举E,再从大到小枚举H,最后从小到大枚举M,取每个值第一个遇到的解。(注意枚举不重复)
“你希望难度差尽量接近”定义一个函数F(x,y,z:longint):longint;
function F(x,y,z:longint):longint; begin exit(abs((a[y]-[x])-(a[z]-a[y]))); end;
接下来是程序:
1 var n,i,j,e,m,h,k:longint; 2 a:array[1..50]of longint; 3 procedure swap(var a,b:longint); 4 var t:longint; 5 begin 6 t:=a; a:=b; b:=t; 7 end; 8 function f(x,y,z:longint):longint; 9 begin 10 exit(abs(abs(a[y]-a[x])-abs(a[z]-a[y]))); 11 end; 12 begin 13 assign(input,‘problemsetter.in‘); 14 assign(output,‘problemsetter.out‘); 15 reset(input); 16 rewrite(output); 17 readln(n); 18 for i:=1 to n do read(a[i]); 19 for i:=1 to n-1 do 20 for j:=i+1 to n do 21 if a[i]>a[j] then swap(a[i],a[j]); 22 E:=1; M:=2; H:=n;//这是所有组合中f最大的! 23 for i:=1 to n do //任意 24 for k:=n downto i+2 do //从最后向前推,注意第i位是E的,第i+1位是M的,所以只能到i+2 25 for j:=i+1 to k-1 do //从E到H(不包含E和H)都可以选 26 if f(i,j,k)<f(E,M,H) then begin 27 E:=i;M:=j;H:=k;//迭代 28 end; 29 writeln(a[E],‘ ‘,a[M],‘ ‘,a[H]);//输出 30 close(input); 31 close(output); 32 end.
这道题需要遵循以下步骤
提供以下样例:
输入:
3 2 1 3 2 1 2 5 5 7 9 3 4 7
输出:
2
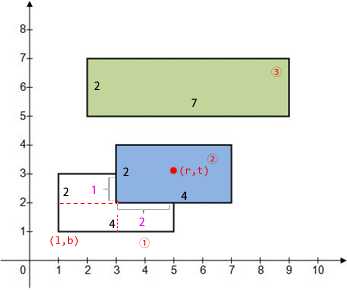
(1)递归求出每一个矩形被覆盖后能看到的面积(注意从后往前枚举,后保存当前编号ans[i])。
定义一个过程:
procedure cal(l,r,b,t,z:longint); //z为从上到下的该层编号(看下还有多少可能的其他编号的矩形在上面)。 begin while (z<=n) and ((r<=x1[z]) or (l>=x2[z]) or (t<=y1[z]) or (b>=y2[z])) do inc(z);//一些不符合条件的矩形 if z>n then begin inc(area[now],(r-l)*(t-b));exit;end; //求出area if l<x1[z] then begin cal(l,x1[z],b,t,z+1);l:=x1[z];end; if r>x2[z] then begin cal(x2[z],r,b,t,z+1);r:=x2[z];end; if b<y1[z] then cal(l,r,b,y1[z],z+1); if t>y2[z] then cal(l,r,y2[z],t,z+1);//分割成四块来求 end;
(2)按面积area从大到小,相同面积按编号从小到大编号排序
for i:=1 to n-1 do for j:=i+1 to n do if (area[i]<area[j])or((area[i]=area[j])and(ans[i]>ans[j])) then begin swap(area[i],area[j]); swap(ans[i],ans[j]); end;
(3)再按编号从小到大对k个编号ans[]排序,这样可以按字典序输出。
for i:=1 to k-1 do for j:=i+1 to k do if ans[i]>ans[j] then swap(ans[i],ans[j]);
完整的程序:
1 var x1,y1,x2,y2,area,ans:array[1..50]of longint; 2 n,k,now,i,j:longint; 3 procedure swap(var a,b:longint); 4 var t:longint; 5 begin 6 t:=a; a:=b; b:=t; 7 end; 8 procedure cal(l,r,b,t,z:longint); 9 begin 10 while (z<=n) and ((r<=x1[z]) or (l>=x2[z]) or (t<=y1[z]) or (b>=y2[z])) do inc(z); 11 if z>n then begin inc(area[now],(r-l)*(t-b));exit;end; 12 if l<x1[z] then begin cal(l,x1[z],b,t,z+1);l:=x1[z];end; 13 if r>x2[z] then begin cal(x2[z],r,b,t,z+1);r:=x2[z];end; 14 if b<y1[z] then cal(l,r,b,y1[z],z+1); 15 if t>y2[z] then cal(l,r,y2[z],t,z+1); 16 end; 17 begin 18 assign(input,‘rectangles.in‘); 19 assign(output,‘rectangles.out‘); 20 reset(input); 21 rewrite(output); 22 readln(n,k); 23 for i:=1 to n do read(x1[i]); readln; 24 for i:=1 to n do read(y1[i]); readln; 25 for i:=1 to n do read(x2[i]); readln; 26 for i:=1 to n do read(y2[i]); readln; 27 for i:=n downto 1 do begin 28 ans[i]:=i; 29 now:=i; 30 cal(x1[now],x2[now],y1[now],y2[now],i+1); 31 end; 32 for i:=1 to n-1 do 33 for j:=i+1 to n do 34 if (area[i]<area[j])or((area[i]=area[j])and(ans[i]>ans[j])) 35 then begin swap(area[i],area[j]); swap(ans[i],ans[j]); end; 36 for i:=1 to k-1 do 37 for j:=i+1 to k do 38 if ans[i]>ans[j] then swap(ans[i],ans[j]); 39 for i:=1 to k-1 do write(ans[i]-1,‘ ‘); 40 writeln(ans[k]-1); 41 close(input); 42 close(output); 43 end.
【枚举算法Day1】20170529-2枚举算法专题练习 题解
标签:proc com 改变 注意 存在 其他 解决 end 组合
原文地址:http://www.cnblogs.com/ljc20020730/p/6918360.html