标签:dm7 ffd rc4 seo vbr oda fps lcx array
如题,已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数数加上x
2.求出某一个数的和
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含2或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数加上k
操作2: 格式:2 x 含义:输出第x个数的值
输出格式:输出包含若干行整数,即为所有操作2的结果。
5 5 1 5 4 2 3 1 2 4 2 2 3 1 1 5 -1 1 3 5 7 2 4
6 10
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=8,M<=10
对于70%的数据:N<=10000,M<=10000
对于100%的数据:N<=500000,M<=500000
样例说明:
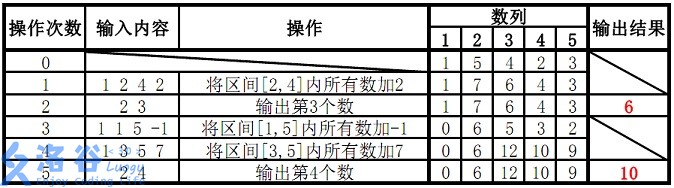
故输出结果为6、10
我们定义$c[i]$表示$a[i]-a[i-1]$就是$a[i]$和$a[i-1]$之间的距离
而且规定$c[1]=a[1]$
那么很明显
$a[i-1]+c[i]=a[i]$
我们把c放入树状数组e里面
## 注意e是树状数组!!!
然后我们可以得出
$query(x)=\sum^{i<=x}_{i=1}c[i]$
$ =c[1]+c[2]+...+c[x-1]+c[x]$
$ =(a[1])+(a[2]-a[1])+...+(a[x-1]-a[x-2])+(a[x]-a[x-1])$
$ =a[1]-a[1]+a[2]+...-a[x-2]+a[x-1]-a[x-1]+a[x]$
$ =a[x]$
刚开始将$c[i]$(也就是$now-last$)插入树状数组就可以啦
因为给$a[x]+z$后
$a[x]$和$a[x-1]$的距离增加了z ,于是我们要给$a[x]-a[x-1]$(即$c[x]$)加上$z$
因为给$a[y]+z$后
$a[y]$和$a[y+1]$的距离减少了z ,于是我们要给$a[y]-a[y+1]$(即$c[y+1]$)加上$-z$
那中间$x<i<y$不用处理?
当然,因为$c[i]$存的只是$a[i]和a[i-1]$的距离啊!
1 program no; 2 var 3 4 n,m,i,now,last,c,x,y,z:Longint; 5 e:array[1..500000] of Longint; 6 7 function lowbit(apple:Longint):Longint ; 8 begin 9 lowbit:=apple and -apple; 10 end; 11 12 procedure add(x,a:Longint); 13 begin 14 while x<=n do 15 begin 16 e[x]:=e[x]+a; 17 x:=x+lowbit(x); 18 end; 19 end; 20 21 function query(x:Longint):longint; 22 begin 23 query:=0; 24 while x>0 do 25 begin 26 query:=query+e[x]; 27 x:=x-lowbit(x); 28 end; 29 end; 30 31 begin 32 //assign(input,‘1.in‘); assign(output,‘1.out‘); 33 reset(input); rewrite(output); 34 35 readln(n,m); 36 for i:= 1 to n do 37 begin 38 read(now); 39 add(i,now-last); 40 last:=now; 41 end; 42 43 for i:= 1 to m do 44 begin 45 read(c,x); 46 if c=1 then 47 begin 48 readln(y,z); 49 add(x,z); 50 add(y+1,-z); 51 end 52 else writeln(query(x)); 53 end; 54 55 close(input); close(output); 56 end.
Luogu P3368 【模板】树状数组 2 [区间修改-单点查询]
标签:dm7 ffd rc4 seo vbr oda fps lcx array
原文地址:http://www.cnblogs.com/tonylim/p/6918610.html