标签:str pts 小技巧 流程 模式 实验 日志 用户 时长
DBSCAN 算法是一种基于密度的聚类算法:
1.聚类的时候不需要预先指定簇的个数
2.最终的簇的个数不确定
DBSCAN算法将数据点分为三类:
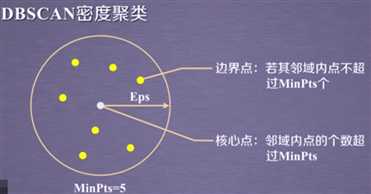
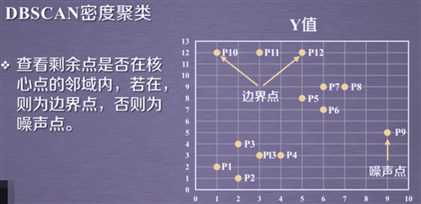
1.核心点:在半径Eps内含有超过MinPts数目的点。
2.边界点:在半径Eps内点的数量小于MinPts,但是落在核心点的邻域内的点。
3.噪音点:既不是核心点也不是边界点的点。
如下图所示:图中黄色的点为边界点,因为在半径Eps内,它领域内的点不超过MinPts个,我们这里设置的MinPts为5;而中间白色的点之所以为核心点,是因为它邻域内的点是超过MinPts(5)个点的,它邻域内的点就是那些黄色的点!
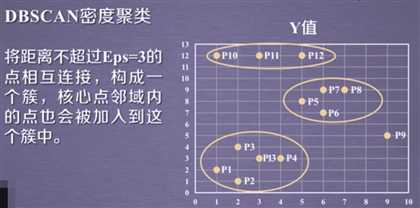
1.将所有点标记为核心点、边界点或噪声点;
2.删除噪声点;
3.为距离在Eps之内的所有核心点之间赋予一条边;
4.每组连通的核心点形成一个簇;
5.将每个边界点指派到一个与之关联的核心点的簇中(哪一个核心点的半径范围之内)。
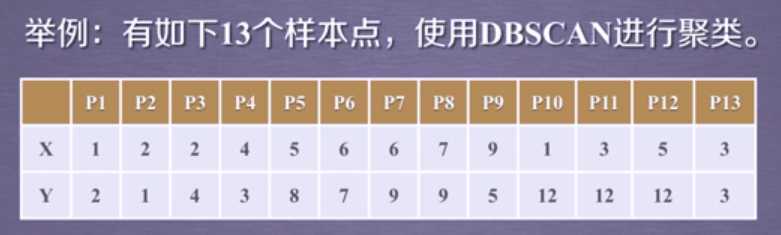
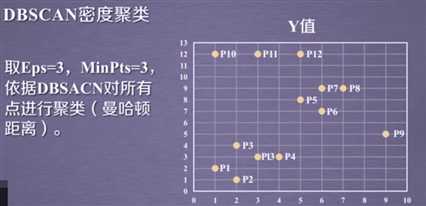
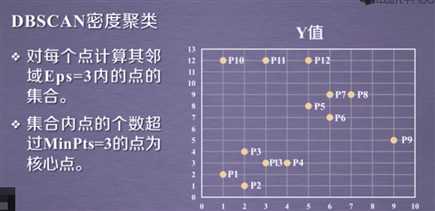
数据介绍
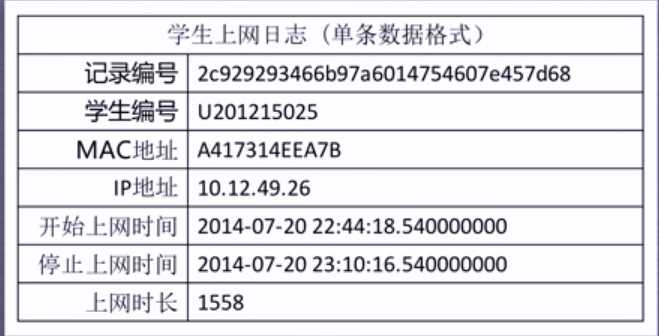
现有大学校园网的日志数据,290条大学生的校园网使用情况数据,数据包括用户ID,设备的MAC地址,IP地址,开始上网时间,停止上网时间,上网时长,校园网套餐等。利用已有数据,分析学生上网的模式。
实验目的
通过DBSCAN聚类,分析学生上网时间和上网时长的模式。
技术路线
采用:sklearn.cluster.DBSCAN 模块
下图为一个数据的实例展示:
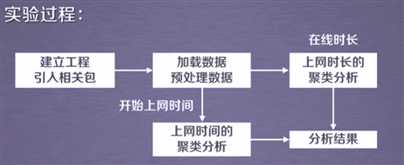
通过上述上网时间的聚类分析和上网时长的聚类分析得出我们想要的同学们上网的时间和时长的分布结果!
1.建立工程,导入sklearn相关包
import numpy as np
from sklearn.cluster import DBSCAN
注意:DBSCAN主要参数:
1.eps:两个样本被看作邻居节点的最大距离
2.min_samples:簇的样本数
3.metric:距离计算方式
例:sklearn.cluster.DBSCAN(eps=0.5,min_samples=5,metric=‘euclidean‘) #euclidean表明我们要采用欧氏距离计算样本点的距离!
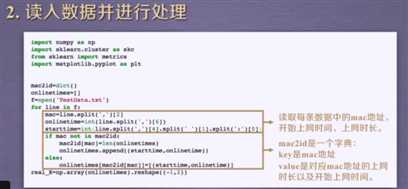
3-1.上网时间聚类,创建DBSCAN算法实例,并进行训练,获得标签:

4.输出标签,查看结果

为了更好的展示结果,我们可以把它画成直方图的形式,便于我们分析;如下我们使用 matplotlib库中的hist函数来进行直方图的展示:
5.画直方图,分析实验结果:

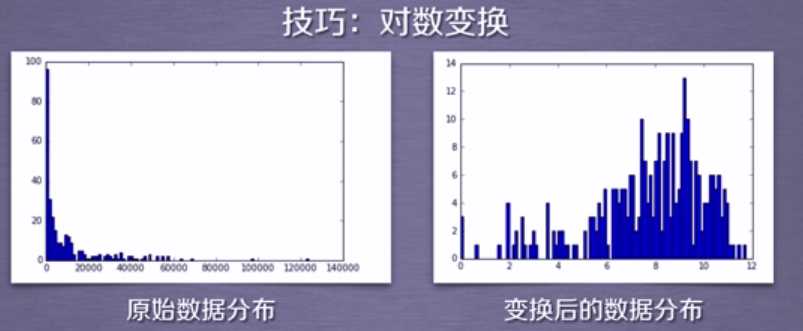
6.数据分布 vs 聚类
这里就是机器学习的一个小技巧了,左边的数据分布不适用于聚类分析的,如果我们想对这类数据进行聚类分析,需要对这些数据进行一些数学变换,通常我们采用取对数的变换方法,将这种数据变换之后,变换后的数据就比较适合用于聚类分析了;
3-2.上网时长聚类,创建DBSCAN算法实例,并进行训练,获得标签:

4-2.输出标签,查看结果

我们也可以看到:时长的聚类效果是不如时间的聚类效果明显的!
标签:str pts 小技巧 流程 模式 实验 日志 用户 时长
原文地址:http://www.cnblogs.com/python-machine/p/6941949.html