多边形区域填充算法－－递归种子填充算法

标签：使用   改进   蓝色   details   没有   orb   图案   领域   替换   

http://blog.csdn.net/orbit/article/details/7323090

     平面区域填充算法是计算机图形学领域的一个很重要的算法，区域填充即给出一个区域的边界（也可以是没有边界，只是给出指定颜色），要求将边界范围内的所有象素单元都修改成指定的颜色（也可能是图案填充）。区域填充中最常用的是多边形填色，本文中我们就讨论几种多边形区域填充算法。

一、种子填充算法（Seed Filling）

        如果要填充的区域是以图像元数据方式给出的，通常使用种子填充算法（Seed Filling）进行区域填充。种子填充算法需要给出图像数据的区域，以及区域内的一个点，这种算法比较适合人机交互方式进行的图像填充操作，不适合计算机自动处理和判断填色。根据对图像区域边界定义方式以及对点的颜色修改方式，种子填充又可细分为几类，比如注入填充算法（Flood Fill Algorithm）、边界填充算法（Boundary Fill Algorithm）以及为减少递归和压栈次数而改进的扫描线种子填充算法等等。

        所有种子填充算法的核心其实就是一个递归算法，都是从指定的种子点开始，向各个方向上搜索，逐个像素进行处理，直到遇到边界，各种种子填充算法只是在处理颜色和边界的方式上有所不同。在开始介绍种子填充算法之前，首先也介绍两个概念，就是“4-联通算法”和“8-联通算法”。既然是搜索就涉及到搜索的方向问题，从区域内任意一点出发，如果只是通过上、下、左、右四个方向搜索到达区域内的任意像素，则用这种方法填充的区域就称为四连通域，这种填充方法就称为“4-联通算法”。如果从区域内任意一点出发，通过上、下、左、右、左上、左下、右上和右下全部八个方向到达区域内的任意像素，则这种方法填充的区域就称为八连通域，这种填充方法就称为“8-联通算法”。如图1（a）所示，假设中心的蓝色点是当前处理的点，如果是“4-联通算法”，则只搜索处理周围蓝色标识的四个点，如果是“8-联通算法”则除了处理上、下、左、右四个蓝色标识的点，还搜索处理四个红色标识的点。两种搜索算法的填充效果分别如如图1（b）和图1（c）所示，假如都是从黄色点开始填充，则“4-联通算法”如图1（b）所示只搜索填充左下角的区域，而“8-联通算法”则如图1（c）所示，将左下角和右上角的区域都填充了。

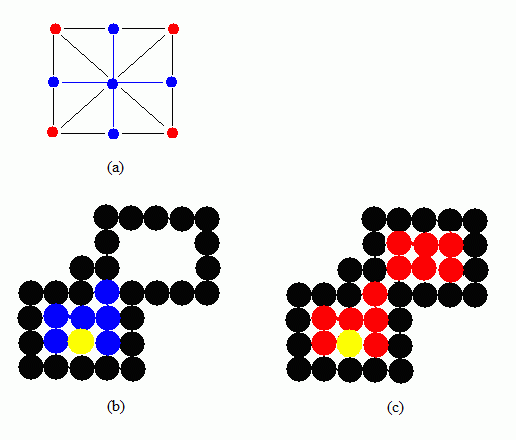
图（1） “4-联通”和“8-联通”填充效果

        并不能仅仅因为图1的填充效果就认为“8-联通算法”一定比“4-联通算法”好，应该根据应用环境和实际的需求选择联通搜索方式，在很多情况下，只有“4-联通算法”才能得到正确的结果。

1.1 注入填充算法（Flood Fill Algorithm）

        注入填充算法不特别强调区域的边界，它只是从指定位置开始，将所有联通区域内某种指定颜色的点都替换成另一种颜色，从而实现填充效果。注入填充算法能够实现颜色替换之类的功能，这在图像处理软件中都得到了广泛的应用。注入填充算法的实现非常简单，核心就是递归和搜索，以下就是注入填充算法的一个实现：

 for循环实现了向8个联通方向的递归搜索，秘密就在direction_8的定义：

这个是搜索类算法中常用的技巧，无需做太多说明，其实只要将其替换成如下direction_4的定义，就可以将算法改成4个联通方向填充算法：

图2就是应用本算法实现的“4-联通”和“8-联通”填充效果：

图（2） 注入填充算法实现

1.2 边界填充算法（Boundary Fill Algorithm）

        边界填充算法与注入填充算法的本质其实是一样的，都是递归和搜索，区别只在于对边界的确认，也就是递归的结束条件不一样。注入填充算法没有边界的概念，只是对联通区域内指定的颜色进行替换，而边界填充算法恰恰强调边界的存在，只要是边界内的点无论是什么颜色，都替换成指定的颜色。边界填充算法在应用上也非常的广泛，画图软件中的“油漆桶”功能就是边界填充算法的例子。以下就是边界填充算法的一个实现：

关于direction_8的说明请参考上一节，图3就是应用本算法实现的“4-联通”和“8-联通”填充效果（其中颜色值是1的点就是指定的边界）：

图（3） 边界填充算法实现

多边形区域填充算法－－递归种子填充算法

标签：使用   改进   蓝色   details   没有   orb   图案   领域   替换   

原文地址：http://www.cnblogs.com/DjangoBlog/p/6950830.html