标签:sub ott 恢复 dex pickle string slist tor turn
优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据。
缺点:可能会产生过度匹配问题。
适用数据类型:数值型和标称型。
创建分支的伪代码函数createBranch()如下所示:
检测数据集中的每个子项是否属于同一分类:
if so return 类标签;
Else
寻找划分数据集的最好特征
划分数据集
创建分支节点
for 每个划分的子集
调用函数createBranch并增加返回结果到分支节点中
return 分支节点
上面的伪代码createBranch是一个递归函数,在倒数第二行直接调用了它自己。后面我们
寄把上面的伪代码转换为Python代码,这里我们需要进一步了解算法是如何划分数据集的。
1 def createDataSet(): 2 dataSet = [[1, 1, ‘yes‘], 3 [1, 1, ‘yes‘], 4 [1, 0, ‘no‘], 5 [0, 1, ‘no‘], 6 [0, 1, ‘no‘]] 7 labels = [‘no surfacing‘,‘flippers‘] 8 #change to discrete values 9 return dataSet, labels
如果看不明白什么是信息增益(information gain)和墒( entropy ),请不要着急—创门自
诞生的那一天起,就注定会令世人十分费解。
嫡定义为信息的期望值,在明晰这个概念之前,我们必须知道信息的定义。如果待分类的事
务可能划分在多个分类之中,则符号xi,的信息定义为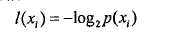
其中P(xi)是选择该分类的概率。
为了计算嫡,我们需要计算所有类别所有可能值包含的信息期望值,通过下面的公式得到:
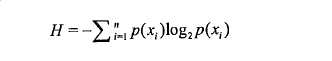
其中n是分类的数目。
程序:计算给定数据集的香农熵
1 def calcShannonEnt(dataSet): 2 numEntries = len(dataSet) #Data 的大小N,N行 3 labelCount = {}#字典存储 不同类别的个数 4 for featVec in dataSet : 5 currentLabel = featVec[-1] #每行的最后一个是类别 6 if currentLabel not in labelCount.keys(): 7 labelCount[currentLabel] = 0 8 labelCount[currentLabel] += 1 #原书缩进错误!!! 9 shannonEnt = 0.0 10 for key in labelCount: 11 prob = float(labelCount[key])/numEntries 12 shannonEnt -= prob *math.log(prob,2) #熵最后外面有个求和符号 !!! 13 return shannonEnt
程序:划分数据集
1 def splitDataSet(dataSet,axis,value): 2 retDataSet = [] 3 for featVec in dataSet: 4 if featVec[axis] == value: 5 #去掉axis 这一列 6 reducedFeatVec = featVec[:axis] 7 reducedFeatVec.extend(featVec[axis+1: ]) 8 retDataSet.append(reducedFeatVec) 9 return retDataSet
划分数据集之后,使得划分后的纯度越小。选择信息增益最大的划分。
程序:选择最好的数据集划分方式
1 def chooseBestFeatureTopSplit(dataSet): 2 #列数 = len(dataset[0]) 3 #行数 = len(dataset) 4 numFeatures = len(dataSet[0]) -1 #最后一列是标签 5 baseEntropy = calcShannonEnt(dataSet) #所有数据的信息熵 6 bestInfoGainn = 0.0 7 bestFeature = -1 8 for i in range(numFeatures):#遍历不同的属性 9 featList = [example[i] for example in dataSet] #取出每一列 10 uniqueVals = set(featList) 11 newEntropy = 0.0 12 for value in uniqueVals:#在第i个属性里,遍历第i个属性所有不同的属性值 13 subDataSet = splitDataSet(dataSet,i,value) #划分数据 14 prob = len(subDataSet)/float(len(dataSet)) #len([[]]) 行数 15 newEntropy += prob *calcShannonEnt(subDataSet) 16 infoGain = baseEntropy - newEntropy 17 if(infoGain > bestInfoGainn): 18 bestInfoGainn = infoGain 19 bestFeature = i 20 return bestFeature
1 def majorityCnt(classList): 2 classCount ={} 3 for vote in classList: 4 if vote not in classCount.keys(): 5 classCount[vote] = 0 6 classCount[vote] += 1 7 8 classCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True) #与python2 不同!!!!!!python3 的字典items 就是迭代对象 9 return classCount[0][0] #返回的是字典第一个元素的key 即 类别标签 10 def createTree(dataSet,labels): 11 #mytree 是一个字典,key 是属性值,val 是类别或者是另一个字典, 12 #如果val 是类标签,则该子节点就是叶子节点 13 #如果val是另一个数据字典,则该节点是一个判断节点 14 classList = [example[-1] for example in dataSet] 15 if classList.count(classList[0]) == len(classList): #类别完全相同,停止划分 16 return classList[0] 17 if len(dataSet[0])==1: #完全划分 18 return majorityCnt(classList) 19 bestFeat = chooseBestFeatureTopSplit(dataSet) 20 bestFeatLabel = labels[bestFeat] 21 myTree = {bestFeatLabel:{}} 22 del(labels[bestFeat]) # 23 featValues = [example[bestFeat] for example in dataSet] # 某属性的所有取值 24 uniqueVals = set(featValues) 25 for value in uniqueVals : 26 subLabels = labels[:] 27 myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels) 28 return myTree
1 #定义文本框跟箭头格式 2 decisionNode = dict(boxstyle="sawtooth", fc="0.8") 3 leafNode = dict(boxstyle="round4", fc="0.8") 4 arrow_args = dict(arrowstyle="<-") 5 def plotNode(nodeTxt, centerPt, parentPt, nodeType): 6 createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords=‘axes fraction‘, 7 xytext=centerPt, textcoords=‘axes fraction‘, 8 va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )
程序:获得叶子节点数与深度
1 def getNumLeafs(myTree): 2 numLeafs = 0 3 firstStr = list(myTree)[0]#找到第一个节点 4 secondDict = myTree[firstStr] #第二个节点 5 for key in secondDict.keys(): #第二节点的字典的key 6 if type(secondDict[key]).__name__==‘dict‘: #判断第二节点是否为字典 7 numLeafs += getNumLeafs(secondDict[key]) #第二节点是字典 ,递归调用getNum 8 else :numLeafs += 1 #第二节点不是字典,说明此节点是最后一个节点 9 return numLeafs 10 11 def getTreeDepth(myTree): 12 maxDepth = 0 13 firstStr = list(myTree)[0]#找到第一个节点 14 secondDict = myTree[firstStr] #第二个节点 15 for key in secondDict.keys(): #第二节点的字典的key 16 if type(secondDict[key]).__name__==‘dict‘: #判断第二节点是否为字典 17 thisDepth = 1 + getTreeDepth(secondDict[key]) #第二节点是字典 ,递归调用getNum 18 else :thisDepth = 1 #第二节点不是字典,说明此节点是最后一个节点 19 if thisDepth > maxDepth: maxDepth =thisDepth 20 return maxDepth
程序:plotTree
1 def plotMidText(cntrPt, parentPt, txtString):#在父子节点间填充文本信息 2 xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0] 3 yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1] 4 createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30) 5 6 def plotTree(myTree, parentPt, nodeTxt): 7 numLeafs = getNumLeafs(myTree) #叶子节点个数 8 depth = getTreeDepth(myTree) #树的高度 9 firstStr = list(myTree)[0] #!!!!!!!与py2不同 10 cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff) #按照叶子结点个数划分x轴 11 plotMidText(cntrPt,parentPt,nodeTxt) 12 plotNode(firstStr,cntrPt,parentPt,decisionNode) 13 secondDict = myTree[firstStr] 14 plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD #plotTree.yOff 全局变量 15 for key in secondDict.keys(): 16 if type(secondDict[key]).__name__ ==‘dict‘: 17 plotTree(secondDict[key],cntrPt,str(key))# 第二节点是字典,递归调用plotTree 18 else: 19 plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW #x方向计算结点坐标 20 plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)#绘制子节点 21 plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))#添加文本信息 22 plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD #下次重新调用时恢复y 23 def createPlot(inTree): 24 fig = plt.figure(1, facecolor=‘white‘) 25 fig.clf() 26 axprops = dict(xticks=[], yticks=[]) 27 createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) # no ticks 28 # createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses 29 plotTree.totalW = float(getNumLeafs(inTree)) 30 plotTree.totalD = float(getTreeDepth(inTree)) 31 plotTree.xOff = -0.5 / plotTree.totalW 32 plotTree.yOff = 1.0 33 plotTree(inTree, (0.5, 1.0), ‘‘) 34 plt.show()
程序:测试
1 def retrieveTree(i): 2 listOfTrees =[{‘no surfacing‘: {0: ‘no‘, 1: {‘flippers‘: {0: ‘no‘, 1: ‘yes‘}}}}, 3 {‘no surfacing‘: {0: ‘no‘, 1: {‘flippers‘: {0: {‘head‘: {0: ‘no‘, 1: ‘yes‘}}, 1: ‘no‘}}}} 4 ] 5 return listOfTrees[i] 6 if __name__ == ‘__main__‘: 7 tree = retrieveTree(0) 8 createPlot(tree)
使用决策树预测隐形眼镜类型
程序:使用决策树分类函数
1 def classify(inputTree,featLabels,testVec): 2 firstStr = list(inputTree.keys())[0] 3 secondDict = inputTree[firstStr] 4 featIndex = featLabels.index(firstStr) #将标签转化成索引 5 for key in secondDict.keys(): 6 if testVec[featIndex] == key: 7 if type(secondDict[key]).__name__==‘dict‘: 8 classLabel = classify(secondDict[key],featLabels,testVec) 9 else : classLabel = secondDict[key]#到达叶子节点,返回标签 10 return classLabel
程序:使用pickle保存模型
1 def storeTree(inputTree,filename): 2 3 with open(filename,‘wb‘) as f: 4 pickle.dump(inputTree,f) 5 6 def grabTree(filename): 7 with open(filename,‘rb‘) as f: 8 t = pickle.load(f) 9 return t
程序:主程序
1 if __name__ == ‘__main__‘: 2 # 3 dataSet,labels = createDataSet() 4 tree = createTree(dataSet,labels) 5 storeTree(tree,"tree.model") 6 tree = grabTree("tree.model") 7 treePlotter.createPlot(tree) 8 9 #读取txt文件,预测隐形眼镜的类型 10 with open(‘lenses.txt‘) as f: 11 lenses = [inst.strip().split(‘\t‘) for inst in f.readlines()] 12 lensesLabels = [‘age‘,‘prescript‘,‘astigmastic‘,‘tearRate‘] 13 lensesTree = createTree(lenses,lensesLabels) 14 treePlotter.createPlot(lensesTree)
标签:sub ott 恢复 dex pickle string slist tor turn
原文地址:http://www.cnblogs.com/zle1992/p/7019512.html