标签：复杂   rom   目的   png   ges   长度   中心   最长回文子串   问题   

本文是我对博友 BIT祝威 和Grandyang ,以及寒小阳关于最长回文子串上关于马拉车算法理解的整理，若是对我的整理有所不懂得，建议去看BIT祝威的博客，很详细，以下纯属个人不成熟的理解。

首先，得先了解什么是回文串（我之前就不是很了解，汗）。回文串就是正反读起来就是一样的，如“abba”。关于采用时间复杂度为O(n^2)，以每个字符为中心去向两端遍历寻找最大回文串的方法，可以见我之前些的博客，戳这里！

当我们遇到字符串为“aaaaaaaaa”，之前的算法就会发生各个回文相互重叠的情况，会产生重复计算，然后就产生了一个问题，能否改进？答案是能，1975年，一个叫Manacher发明了Manacher Algorithm算法，俗称马拉车算法，其时间复杂为O(n)。该算法是利用回文串的特性来避免重复计算的，至于如何利用，且由后面慢慢道来。

在时间复杂度为O(n^2)的算法中，我们在遍历的过程要考虑到回文串长度的奇偶性，比如说“abba”的长度为偶数，“abcba”的长度为奇数，这样在寻找最长回文子串的过程要分别考奇偶的情况，是否可以统一处理了？

马拉车算法：

1）的第一步是改造字符串S，变为T，其改造的方法如下：

在字符串S的字符之间和S的首尾都插入一个“#”，如：S=“abba”变为T="#a#b#b#a#" 。我们会发现S的长度是4，而T的长度为9，长度变为奇数了！！那S的长度为奇数的情况时，变化后的长度还是奇数吗？我们举个例子，S=“abcba”，变化为T=“#a#b#c#b#a#”，T的长度为11，所以我们发现其改造的目的是将字符串的长度变为奇数，这样就可以统一的处理奇偶的情况了。

2）第二步，为了改进回文相互重叠的情况，我们将改造完后的T[ i ] 处的回文半径存储到数组P[ ]中，P[ i ]为新字符串T的T[ i ]处的回文长度，表示以字符T[i]为中心的最长回文字串的最端右字符到T[i]的长度，如以T[ i ]为中心的最长回文子串的为T[ l, r ]，那么P[ i ]=r-i+1。这样最后遍历数组P[ ]，取其最大值即可。若P[ i ]=1表示该回文串就是T[ i  ]本身。举一个简单的例子感受一下：

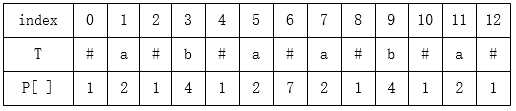
数组P有一性质，P[ i ]-1就是该回文子串在原字符串S中的长度 ，那就是P[i]-1就是该回文子串在原字符串S中的长度，至于证明，首先在转换得到的字符串T中，所有的回文字串的长度都为奇数，那么对于以T[i]为中心的最长回文字串，其长度就为2*P[i]-1,经过观察可知，T中所有的回文子串，其中分隔符的数量一定比其他字符的数量多1，也就是有P[i]个分隔符，剩下P[i]-1个字符来自原字符串，所以该回文串在原字符串中的长度就为P[i]-1。【这段解释引用 dyx心心】

另外，由于第一个和最后一个字符都是#号，且也需要搜索回文，为了防止越界，我们还需要在首尾再加上非#号字符，实际操作时我们只需给开头加上个非#号字符，结尾不用加的原因是字符串的结尾标识为‘\0‘，等于默认加过了。这样原问题就转化成如何求数组P[ ]的问题了。

3）如何求数组P [ ]

待续.....睡觉了，明天补上

Manacher's Algorithm ----马拉车算法

标签：复杂   rom   目的   png   ges   长度   中心   最长回文子串   问题   

原文地址：http://www.cnblogs.com/love-yh/p/7072161.html